在鍊錶中插入最大公約數

2807。在鍊錶中插入最大公約數

難度：中

主題：鍊錶、數學、數論

給定一個鍊錶頭，其中每個節點都包含一個整數值。

在每對相鄰節點之間，插入一個新節點，其值等於它們的最大公約數。

回傳插入後的鍊錶.

兩個數的最大公約數是能整除兩個數的最大正整數。

範例1：

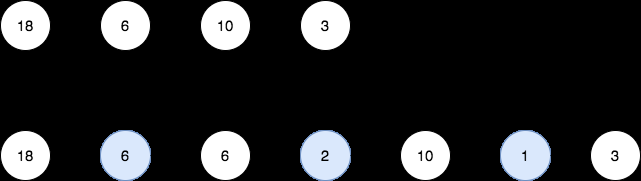
• 輸入： head = [18,6,10,3]
• 輸出： [18,6,6,2,10,1,3]
• 說明：第1^st圖表示初始鍊錶，第2^nd圖表示插入新節點後的鍊錶（藍色的節點是插入的節點）節點）。
  • 我們在第 1^st 和 2^nd 節點之間插入 18 和 6 = 6 的最大公約數。
  • 我們在第 2^nd 和第 3^rd 節點之間插入 6 和 10 = 2 的最大公約數。
  • 我們在第 3^rd 和第 4^th 節點之間插入 10 和 3 = 1 的最大公約數。 沒有更多的相鄰節點，因此我們返回鍊錶。

範例2：

• 輸入： head = [7]
• 輸出： [7]
• 說明：第1^st圖表示初始鍊錶，第2^nd圖表示插入新節點後的鍊錶。 沒有成對的相鄰節點，因此我們傳回初始鍊錶。

範例 3：

• 輸入： 成本= [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
• 輸出： 10

約束：

• 清單中的節點數量在 [1, 5000] 範圍內。
• 1

提示：

1. 左側的每個點要麼連接到已連接到某個左側節點的精確點，要麼連接到右側未連接到任何節點的節點的子集
2. 使用帶有位元遮罩的動態規劃，其中狀態將為（第一組中分配的點的數量，第二組中分配的點的位元遮罩）。

解：

我們需要在鍊錶中的每對相鄰節點之間插入節點。插入節點的值應該是兩個相鄰節點值的最大公約數（GCD）。我們將遍歷鍊錶，計算每對相鄰節點的 GCD，然後相應地插入新節點。

以下是解決此問題的方法：

1. 定義一個ListNode類別：該類別將代表鍊錶中的每個節點。
2. 遍歷列表：我們將迭代列表以查找每對相鄰節點。
3. 插入 GCD 節點：對於每對相鄰節點，我們將插入一個新節點，其值為兩個相鄰節點的 GCD。
4. 回傳修改後的清單.

讓我們用 PHP 實作這個解決方案：2807。在鍊錶中插入最大公約數

<?php
// Definition for a singly-linked list node.
class ListNode {
    public $val = 0;
    public $next = null;

    public function __construct($val = 0, $next = null) {
        $this->val = $val;
        $this->next = $next;
    }
}

/**
 * Function to calculate the GCD of two numbers.
 *
 * @param $a
 * @param $b
 * @return mixed
 */
function gcd($a, $b) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */

}

/**
 * @param ListNode $head
 * @return ListNode
 */
function insertGreatestCommonDivisors($head) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * Function to print the linked list for testing purposes.
 * 
 * @param $head
 * @return void
 */
function printList($head) {
    $current = $head;
    while ($current != null) {
        echo $current->val . " ";
        $current = $current->next;
    }
    echo "\n";
}

// Example usage:

// Create the linked list: 18 -> 6 -> 10 -> 3
$head = new ListNode(18);
$head->next = new ListNode(6);
$head->next->next = new ListNode(10);
$head->next->next->next = new ListNode(3);

// Insert GCD nodes.
$modifiedHead = insertGreatestCommonDivisors($head);

// Print the modified linked list.
printList($modifiedHead);

// Output should be: 18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3
?>

解釋：

1. ListNode 類別：此類別表示鍊錶中節點的結構，具有值 ($val) 和下一個節點 ($next) 的屬性。

2. GCD 計算：gcd 函數使用歐幾里德演算法計算兩個整數的最大公約數。

3. 主要邏輯（插入最大公約數）:

   • 我們循環遍歷鍊錶，直到到達倒數第二個節點。
   • 對於每對相鄰節點，我們計算它們值的 GCD。
   • 我們使用此 GCD 值建立一個新節點並將其插入當前節點和下一個節點之間。

4. 邊緣情況：如果清單只有一個節點，我們將按原樣返回它，不做任何更改，因為沒有相鄰節點。

5. 測試：函數 printList 是一個輔助函數，用於輸出鍊錶的值以進行驗證。

Time Complexity:

• The time complexity of this solution is (O(n)), where (n) is the number of nodes in the linked list. Calculating the GCD for each adjacent pair takes constant time on average, and we perform a linear traversal of the list.

Example:

For the input list [18, 6, 10, 3], the output is:

18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!

If you want more helpful content like this, feel free to follow me:

• LinkedIn
• GitHub

以上是在鍊錶中插入最大公約數的詳細內容。更多資訊請關注PHP中文網其他相關文章！