尋找最短路徑

兩個頂點之間的最短路徑是總權重最小的路徑。
給定一個邊上具有非負權重的圖，荷蘭計算機科學家 Edsger Dijkstra 發現了一種著名的演算法，用於查找兩個頂點之間的最短路徑。為了找到從頂點 s 到頂點 v 的最短路徑，Dijkstra 演算法 找到從 s 到所有頂點的最短路徑。因此迪傑斯特拉演算法稱為單源最短路徑演算法。此演算法使用 cost[v] 來儲存從頂點 v 到來源頂點 s 的 最短路徑 的成本。 成本[s]為0。最初將無窮大分配給所有其他頂點的 cost[v]。演算法重複地在V – T 中尋找cost[u] 最小的頂點u 並將u 移到 T .

演算法在下面的程式碼中描述。

Input: a graph G = (V, E) with non-negative weights
Output: a shortest path tree with the source vertex s as the root
 1 ShortestPathTree getShortestPath(s) {
 2 Let T be a set that contains the vertices whose
 3 paths to s are known; Initially T is empty;
 4 Set cost[s] = 0; and cost[v] = infinity for all other vertices in V;
 5
 6 while (size of T < n) {
 7 Find u not in T with the smallest cost[u];
 8 Add u to T;
 9 for (each v not in T and (u, v) in E)
10 if (cost[v] > cost[u] + w(u, v)) {
11 cost[v] = cost[u] + w(u, v); parent[v] = u;
12 }
13 }
14 }

這個演算法與 Prim 尋找最小生成樹的演算法非常相似。兩種演算法都將頂點分為兩個集合：T 和 V - T。在 Prim 演算法的情況下，集合 T 包含已新增至樹中的頂點。在 Dijkstra 的情況下，集合 T 包含已找到到來源的最短路徑的頂點。兩種演算法都會重複從 V – T 中尋找頂點並將其新增至 T。在 Prim 演算法的情況下，頂點與集合中邊緣權重最小的某個頂點相鄰。在 Dijkstra 演算法中，該頂點與集合中某頂點相鄰，且對來源的總成本最小。

演算法首先將 cost[s] 設為 0（第 4 行），將所有其他頂點的 cost[v] 設為無窮大。然後，它不斷地將一個頂點（例如u）從V – T 加入T 中，且cost[u]最小（第7 行– 8）、如下圖a．將u 加入T 後，演算法會更新每個vcost[v] 和parent[v] > 不在T 中，如果(u, v) 位於T 且cost[v] > cost[u] + w(u , v)（第10-11 行）。

讓我們使用下圖a的圖來說明Dijkstra演算法。假設源頂點是

1。因此，cost[1] = 0 而所有其他頂點的成本最初為 ∞，如下圖 b 所示。我們使用 parent[i] 來表示路徑中 i 的父級。為了方便起見，將來源節點的父節點設定為 -1.

初始設定

T為空。此演算法選擇成本最小的頂點。在本例中，頂點為 1。演算法將1加到T，如下圖a所示。然後，它會調整與 1 相鄰的每個頂點的成本。現在更新了頂點 2、0、6、3 及其父節點的成本，如下圖 b.

頂點

2、0、6 和3 與來源頂點相鄰，且頂點2是V-T 中成本最小的一個，因此將2 添加到T，如下圖所示，並更新中頂點的成本和父級 V-T 並與2 相鄰。 cost[0] 現已更新為 6，其父級設定為 2。從1到2的箭頭線表示將2加到後，1是2的父級T.

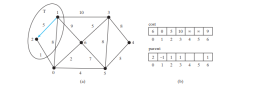
現在 T 包含 {1, 2}。頂點0 是V-T 中成本最小的頂點，因此將0 加入T，如下圖所示，並更新V-T 中且與0 相鄰的頂點的成本和父級（如果適用）。 cost[5] 現已更新為10，其父項設定為0，cost[6] 現已更新為8 及其父級設定為0.

現在 T 包含 {1, 2, 0}。頂點6 是V-T 中成本最小的頂點，因此將6 加入T，如下圖所示，並更新V-T 中且與6 相鄰的頂點的成本和父級（如果適用）。

現在 T 包含 {1, 2, 0, 6}。頂點 3 或 5 是 V-T 中成本最小的一個。您可以將 3 或 5 加入到 T 中。讓我們將3 添加到T，如下圖所示，並更新V-T 中且與3 相鄰的頂點的成本和父級如果適用。 cost[4] 現已更新為 18，其父級設定為 3。

現在T 包含{1, 2, 0, 6, 3}。頂點5 是V-T 中成本最小的頂點，因此將5 加入T，如下圖所示，並更新V-T 中且與5 相鄰的頂點的成本和父級（如果適用）。 cost[4] 現已更新為 10，其父級設定為 5。

現在T 包含{1, 2, 0, 6, 3，5}。頂點 4 是 V-T 中成本最小的頂點，因此將 4 加入 T，如下圖所示。

如您所見，該演算法本質上是從來源頂點找到所有最短路徑，從而產生以來源頂點為根的樹。我們將此樹稱為單源全最短路徑樹（或簡稱最短路徑樹）。要對此樹建模，請定義一個名為 ShortestPathTree 的類，該類擴展 Tree 類，如下圖所示。 ShortestPathTree 定義為 WeightedGraph.java 中第 200-224 行 WeightedGraph 中的內部類別。

getShortestPath(int sourceVertex) 方法在 WeightedGraph.java 的第 156-197 行實現。此方法將所有其他頂點的cost[sourceVertex] 設為0 （第162 行），並將cost[v] 設定為無窮大（第159 -161 行）。 sourceVertex 的父級設定為 -1（第 166 行）。 T 是一個列表，儲存加入最短路徑樹中的頂點（第 169 行）。我們使用 T 的列表而不是集合來記錄添加到 T 的頂點的順序。

最初，T 是空的。要展開 T，該方法執行以下操作：

1. Find the vertex u with the smallest cost[u] (lines 175–181) and add it into T (line 183).
2. After adding u in T, update cost[v] and parent[v] for each v adjacent to u in V-T if cost[v] > cost[u] + w(u, v) (lines 186–192).

Once all vertices from s are added to T, an instance of ShortestPathTree is created (line 196).

The ShortestPathTree class extends the Tree class (line 200). To create an instance of ShortestPathTree, pass sourceVertex, parent, T, and cost (lines 204–205). sourceVertex becomes the root in the tree. The data fields root, parent, and searchOrder are defined in the Tree class, which is an inner class defined in AbstractGraph.

Note that testing whether a vertex i is in T by invoking T.contains(i) takes O(n) time, since T is a list. Therefore, the overall time complexity for this implemention is O(n^3).

Dijkstra’s algorithm is a combination of a greedy algorithm and dynamic programming. It is a greedy algorithm in the sense that it always adds a new vertex that has the shortest distance to the source. It stores the shortest distance of each known vertex to the source and uses it later to avoid redundant computing, so Dijkstra’s algorithm also uses dynamic programming.

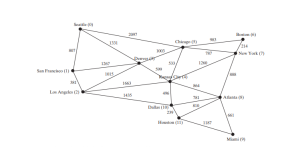
The code below gives a test program that displays the shortest paths from Chicago to all other cities in Figure below and the shortest paths from vertex 3 to all vertices for the graph in Figure below a, respectively.

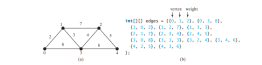
package demo;

public class TestShortestPath {

    public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<String> graph1 = new WeightedGraph<>(vertices, edges);
        WeightedGraph<String>.ShortestPathTree tree1 = graph1.getShortestPath(graph1.getIndex("Chicago"));
        tree1.printAllPaths();

        // Display shortest paths from Houston to Chicago       
        System.out.println("Shortest path from Houston to Chicago: ");
        java.util.List<String> path = tree1.getPath(graph1.getIndex("Houston"));
        for(String s: path) {
            System.out.print(s + " ");
        }

        edges = new int[][]{
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };

        WeightedGraph<Integer> graph2 = new WeightedGraph<>(edges, 5);
        WeightedGraph<Integer>.ShortestPathTree tree2 = graph2.getShortestPath(3);
        System.out.println("\n");
        tree2.printAllPaths();
    }

}

All shortest paths from Chicago are:
A path from Chicago to Seattle: Chicago Seattle (cost: 2097.0)
A path from Chicago to San Francisco:
Chicago Denver San Francisco (cost: 2270.0)
A path from Chicago to Los Angeles:
Chicago Denver Los Angeles (cost: 2018.0)
A path from Chicago to Denver: Chicago Denver (cost: 1003.0)
A path from Chicago to Kansas City: Chicago Kansas City (cost: 533.0)
A path from Chicago to Chicago: Chicago (cost: 0.0)
A path from Chicago to Boston: Chicago Boston (cost: 983.0)
A path from Chicago to New York: Chicago New York (cost: 787.0)
A path from Chicago to Atlanta:
Chicago Kansas City Atlanta (cost: 1397.0)
A path from Chicago to Miami:
Chicago Kansas City Atlanta Miami (cost: 2058.0)
A path from Chicago to Dallas: Chicago Kansas City Dallas (cost: 1029.0)
A path from Chicago to Houston:
Chicago Kansas City Dallas Houston (cost: 1268.0)
Shortest path from Houston to Chicago:
Houston Dallas Kansas City Chicago

All shortest paths from 3 are:
A path from 3 to 0: 3 1 0 (cost: 5.0)
A path from 3 to 1: 3 1 (cost: 3.0)
A path from 3 to 2: 3 2 (cost: 4.0)
A path from 3 to 3: 3 (cost: 0.0)
A path from 3 to 4: 3 4 (cost: 6.0)

The program creates a weighted graph for Figure above in line 27. It then invokes the getShortestPath(graph1.getIndex("Chicago")) method to return a Path object that contains all shortest paths from Chicago. Invoking printAllPaths() on the ShortestPathTree object displays all the paths (line 30).

The graphical illustration of all shortest paths from Chicago is shown in Figure below. The shortest paths from Chicago to the cities are found in this order: Kansas City, New York, Boston, Denver, Dallas, Houston, Atlanta, Los Angeles, Miami, Seattle, and San Francisco.

以上是尋找最短路徑的詳細內容。更多資訊請關注PHP中文網其他相關文章！