介紹
圖是一種資料結構,具有多個頂點(節點)和它們之間的邊(連接)。
樹是圖的一個例子。每棵樹都是一個圖,但並非每個圖都是樹,例如,有環的圖就不是樹。一棵樹將有一個根和兩個節點之間的一條唯一路徑,而圖可以有多個根和頂點之間的多個路徑。
基本術語
頂點: 圖中的節點。
邊: 兩個頂點之間的連接。
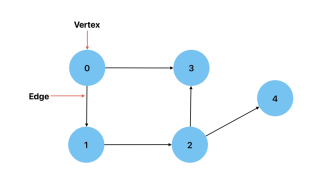
有向: 當兩個頂點之間的連接有方向時。這意味著只有一種方法可以從一個頂點到達另一個頂點。一個例子是顯示城市(頂點)和它們之間的路線(邊)的圖表。
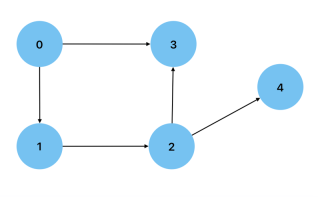
無向: 當圖上兩個頂點之間的連接是雙向的。一個例子是顯示透過友誼連結的人(頂點)的圖表。
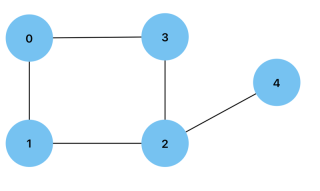
度數: 連接到頂點的邊數。有向圖的頂點可以有入度或出度,分別是指向和遠離頂點的邊的數量。
加權: 邊的值作為權重的圖。一個例子是路線圖,其中節點之間的距離表示為權重。
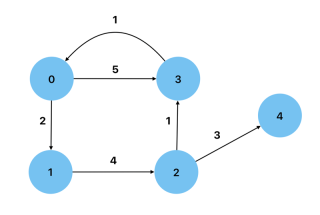
循環: 具有從至少一個頂點返回自身的路徑的圖。
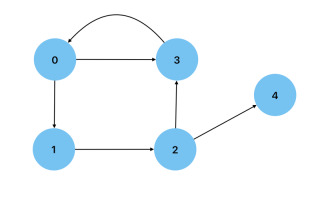
非循環: 沒有循環的圖,也就是說,沒有節點有回自身的路徑。 有向無環圖是一種可用來顯示資料處理流程的圖。
密集:當圖的邊數接近最大可能數時
稀疏: 當圖的邊數接近最小可能數量時。
自循環: 當一條邊有一個頂點連結到其自身時。
多邊: 當圖在兩個頂點之間具有多條邊時。
簡單:當圖沒有自環或多邊時。
取得簡單有向圖中的最大邊數:n*(n-1),其中 n 是節點數。
要取得簡單無向圖中的最大邊數:n*(n-1)/2,其中 n 是節點數。
在 JavaScript 中實作圖表
要實現圖,我們可以從指定圖的頂點和邊開始,下面是如何在給定圖的情況下執行此操作的範例:
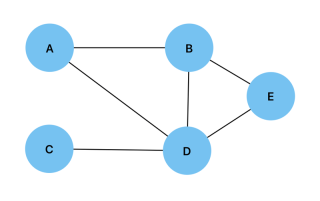
const vertices = ["A", "B", "C", "D", "E"]; const edges = [ ["A", "B"], ["A", "D"], ["B", "D"], ["B", "E"], ["C", "D"], ["D", "E"], ];
然後我們可以建立一個函數來尋找與給定頂點相鄰的內容:
const findAdjacentNodes = function (node) {
const adjacentNodes = [];
for (let edge of edges) {
const nodeIndex = edge.indexOf(node);
if (nodeIndex > -1) {
let adjacentNode = nodeIndex === 0 ? edge[1] : edge[0];
adjacentNodes.push(adjacentNode);
}
}
return adjacentNodes;
};
還有另一個檢查兩個頂點是否連接的函數:
const isConnected = function (node1, node2) {
const adjacentNodes = new Set(findAdjacentNodes(node1));
return adjacentNodes.has(node2);
};
鄰接表
鄰接清單是圖的表示形式,其中連接到節點的所有頂點都儲存為清單。下面是一個圖表及其對應鄰接清單的直觀表示。


鄰接列表可以透過建立兩個類別(Node 類別和 Graph 類別)在 JavaScript 中實現。 Node 類別將包含一個建構函式和一個連接兩個頂點的 connect() 方法。它還具有 isConnected() 和 getAdjacentNodes() 方法,其工作方式與上面所示的完全相同。
class Node {
constructor(value) {
this.value = value;
this.edgesList = [];
}
connect(node) {
this.edgesList.push(node);
node.edgesList.push(this);
}
getAdjNodes() {
return this.edgesList.map((edge) => edge.value);
}
isConnected(node) {
return this.edgesList.map((edge) =>
edge.value).indexOf(node.value) > -1;
}
}
Graph 類別由建構子和 addToGraph() 方法組成,該方法會為圖中新增頂點。
class Graph {
constructor(nodes) {
this.nodes = [...nodes];
}
addToGraph(node) {
this.nodes.push(node);
}
}
Adjacency Matrix
A 2-D array where each array represents a vertex and each index represents a possible connection between vertices. An adjacency matrix is filled with 0s and 1s, with 1 representing a connection. The value at adjacencyMatrix[node1][node2] will show whether or not there is a connection between the two specified vertices. Below is is a graph and its visual representation as an adjacency matrix.


To implement this adjacency matrix in JavaScript, we start by creating two classes, the first being the Node class:
class Node {
constructor(value) {
this.value = value;
}
}
We then create the Graph class which will contain the constructor for creating the 2-D array initialized with zeros.
class Graph {
constructor(nodes) {
this.nodes = [...nodes];
this.adjacencyMatrix = Array.from({ length: nodes.length },
() => Array(nodes.length).fill(0));
}
}
We will then add the addNode() method which will be used to add new vertices to the graph.
addNode(node) {
this.nodes.push(node);
this.adjacencyMatrix.forEach((row) => row.push(0));
this.adjacencyMatrix.push(new Array(this.nodes.length).fill(0));
}
Next is the connect() method which will add an edge between two vertices.
connect(node1, node2) {
const index1 = this.nodes.indexOf(node1);
const index2 = this.nodes.indexOf(node2);
if (index1 > -1 && index2 > -1) {
this.adjacencyMatrix[index1][index2] = 1;
this.adjacencyMatrix[index2][index1] = 1;
}
}
We will also create the isConnected() method which can be used to check if two vertices are connected.
isConnected(node1, node2) {
const index1 = this.nodes.indexOf(node1);
const index2 = this.nodes.indexOf(node2);
if (index1 > -1 && index2 > -1) {
return this.adjacencyMatrix[index1][index2] === 1;
}
return false;
}
Lastly we will add the printAdjacencyMatrix() method to the Graph class.
printAdjacencyMatrix() {
console.log(this.adjacencyMatrix);
}
Breadth First Search
Similar to a Breadth First Search in a tree, the vertices adjacent to the current vertex are visited before visiting any subsequent children. A queue is the data structure of choice when performing a Breadth First Search on a graph.
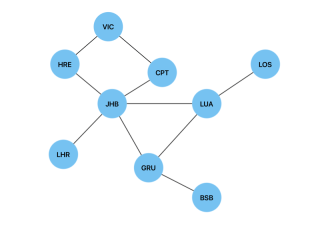
Below is a graph of international airports and their connections and we will use a Breadth First Search to find the shortest route(path) between two airports(vertices).
In order to implement this search algorithm in JavaScript, we will use the same Node and Graph classes we implemented the adjacency list above. We will create a breadthFirstTraversal() method and add it to the Graph class in order to traverse between two given vertices. This method will have the visitedNodes object, which will be used to store the visited vertices and their predecessors. It is initiated as null to show that the first vertex in our search has no predecessors.
breathFirstTraversal(start, end) {
const queue = [start];
const visitedNodes = {};
visitedNodes[start.value] = null;
while (queue.length > 0) {
const node = queue.shift();
if (node.value === end.value) {
return this.reconstructedPath(visitedNodes, end);
}
for (const adjacency of node.edgesList) {
if (!visitedNodes.hasOwnProperty(adjacency.value)) {
visitedNodes[adjacency.value] = node;
queue.push(adjacency);
}
}
}
}
Once the end vertex is found, we will use the reconstructedPath() method in the Graph class in order to return the shortest path between two vertices. Each vertex is added iteratively to the shortestPath array, which in turn must be reversed in order to come up with the correct order for the shortest path.
reconstructedPath(visitedNodes, endNode) {
let currNode = endNode;
const shortestPath = [];
while (currNode !== null) {
shortestPath.push(currNode.value);
currNode = visitedNodes[currNode.value];
}
return shortestPath.reverse();
}
In the case of the graph of international airports, breathFirstTraversal(JHB, LOS) will return JHB -> LUA -> LOS as the shortest path. In the case of a weighted graph, we would use Dijkstra's algorithm to find the shortest path.
Depth First Search
Similar to a depth first search in a tree, this algorithm will fully explore every descendant of a vertex, before backtracking to the root. A stack is the data structure of choice for depth first traversals in a graph.
A depth first search can be used to detect a cycle in a graph. We will use the same graph of international airports to illustrate this in JavaScript.

Similar to the Breadth First Search algorithm above, this implementation of a Depth First Search algorithm in JavaScript will use the previously created Node and Graph classes. We will create a helper function called depthFirstTraversal() and add it to the Graph class.
depthFirstTraversal(start, visitedNodes = {}, parent = null) {
visitedNodes[start.value] = true;
for (const adjacency of start.edgesList) {
if (!visitedNodes[adjacency.value]) {
if (this.depthFirstTraversal(adjacency, visitedNodes, start)) {
return true;
}
} else if (adjacency !== parent) {
return true;
}
}
return false;
}
This will perform the Depth First Traversal of the graph, using the parent parameter to keep track of the previous vertex and prevent the detection of a cycle when revisiting the parent vertex. Visited vertices will be marked as true in the visitedNodes object. This method will then use recursion to visit previously unvisited vertices. If the vertex has already been visited, we check it against the parent parameter. A cycle has been found if the vertex has already been visited and it is not the parent.
We will also create the wrapper function hasCycle() in the Graph class. This function is used to detect a cycle in a disconnected graph. It will initialize the visitedNodes object and loop through all of the vertices in the graph.
hasCycle() {
const visitedNodes = {};
for (const node of this.nodes) {
if (!visitedNodes[node.value]) {
if (this.depthFirstTraversal(node, visitedNodes)) {
return true;
}
}
}
return false;
}
In the case of the graph of international airports, the code will return true.
Depth First Traversal of a graph is also useful for pathfinding(not necessarily shortest path) and for solving mazes.
Conclusion
A firm understanding of graphs as a data structure and of their associated algorithms is absolutely necessary when furthering one's studies of data structures and algorithms. Although not as beginner friendly as the previous posts in this series, this guide should prove useful to deepen your understanding of data structures and algorithms.
以上是資料結構與演算法:圖的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 JavaScript評論:使用//和 / * * / * / * /May 13, 2025 pm 03:49 PM
JavaScript評論:使用//和 / * * / * / * /May 13, 2025 pm 03:49 PMJavaScriptusestwotypesofcomments:single-line(//)andmulti-line(//).1)Use//forquicknotesorsingle-lineexplanations.2)Use//forlongerexplanationsorcommentingoutblocksofcode.Commentsshouldexplainthe'why',notthe'what',andbeplacedabovetherelevantcodeforclari
 Python vs. JavaScript:開發人員的比較分析May 09, 2025 am 12:22 AM
Python vs. JavaScript:開發人員的比較分析May 09, 2025 am 12:22 AMPython和JavaScript的主要區別在於類型系統和應用場景。 1.Python使用動態類型,適合科學計算和數據分析。 2.JavaScript採用弱類型,廣泛用於前端和全棧開發。兩者在異步編程和性能優化上各有優勢,選擇時應根據項目需求決定。
 Python vs. JavaScript:選擇合適的工具May 08, 2025 am 12:10 AM
Python vs. JavaScript:選擇合適的工具May 08, 2025 am 12:10 AM選擇Python還是JavaScript取決於項目類型:1)數據科學和自動化任務選擇Python;2)前端和全棧開發選擇JavaScript。 Python因其在數據處理和自動化方面的強大庫而備受青睞,而JavaScript則因其在網頁交互和全棧開發中的優勢而不可或缺。
 Python和JavaScript:了解每個的優勢May 06, 2025 am 12:15 AM
Python和JavaScript:了解每個的優勢May 06, 2025 am 12:15 AMPython和JavaScript各有優勢,選擇取決於項目需求和個人偏好。 1.Python易學,語法簡潔,適用於數據科學和後端開發,但執行速度較慢。 2.JavaScript在前端開發中無處不在,異步編程能力強,Node.js使其適用於全棧開發,但語法可能複雜且易出錯。
 JavaScript的核心:它是在C還是C上構建的?May 05, 2025 am 12:07 AM
JavaScript的核心:它是在C還是C上構建的?May 05, 2025 am 12:07 AMjavascriptisnotbuiltoncorc; sanInterpretedlanguagethatrunsonenginesoftenwritteninc.1)JavascriptwasdesignedAsignedAsalightWeight,drackendedlanguageforwebbrowsers.2)Enginesevolvedfromsimpleterterpretpretpretpretpreterterpretpretpretpretpretpretpretpretpretcompilerers,典型地,替代品。
 JavaScript應用程序:從前端到後端May 04, 2025 am 12:12 AM
JavaScript應用程序:從前端到後端May 04, 2025 am 12:12 AMJavaScript可用於前端和後端開發。前端通過DOM操作增強用戶體驗,後端通過Node.js處理服務器任務。 1.前端示例:改變網頁文本內容。 2.後端示例:創建Node.js服務器。
 Python vs. JavaScript:您應該學到哪種語言?May 03, 2025 am 12:10 AM
Python vs. JavaScript:您應該學到哪種語言?May 03, 2025 am 12:10 AM選擇Python還是JavaScript應基於職業發展、學習曲線和生態系統:1)職業發展:Python適合數據科學和後端開發,JavaScript適合前端和全棧開發。 2)學習曲線:Python語法簡潔,適合初學者;JavaScript語法靈活。 3)生態系統:Python有豐富的科學計算庫,JavaScript有強大的前端框架。
 JavaScript框架:為現代網絡開發提供動力May 02, 2025 am 12:04 AM
JavaScript框架:為現代網絡開發提供動力May 02, 2025 am 12:04 AMJavaScript框架的強大之處在於簡化開發、提升用戶體驗和應用性能。選擇框架時應考慮:1.項目規模和復雜度,2.團隊經驗,3.生態系統和社區支持。


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境

SecLists
SecLists是最終安全測試人員的伙伴。它是一個包含各種類型清單的集合,這些清單在安全評估過程中經常使用,而且都在一個地方。 SecLists透過方便地提供安全測試人員可能需要的所有列表,幫助提高安全測試的效率和生產力。清單類型包括使用者名稱、密碼、URL、模糊測試有效載荷、敏感資料模式、Web shell等等。測試人員只需將此儲存庫拉到新的測試機上,他就可以存取所需的每種類型的清單。

Dreamweaver Mac版
視覺化網頁開發工具

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3漢化版
中文版,非常好用





