連接兩組點的最低成本
- 王林原創
- 2024-09-01 06:34:061180瀏覽
1595。連接兩組點的最低成本
難度:難
主題:陣列、動態規劃、位元操作、矩陣、位元遮罩
您將獲得兩組點,其中第一組大小為1 點,第二組大小為2 點,大小為1 > 點。 = 大小2.
任兩點之間的連接成本以大小1 x size2 矩陣給出,其中cost[i][j] 是連接點i 的成本第一組和第二組的j 點。如果兩組中的每個點都連接到相反組中的一個或多個點,則這些組已連接。換句話說,第一組中的每個點必須連接到第二組中的至少一個點,第二組中的每個點必須連接到第一組中的至少一個點。
回傳連接兩組所需的最低成本。
範例1:
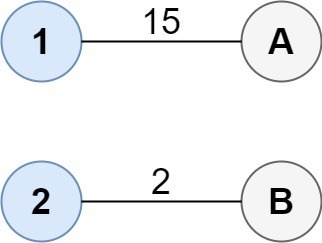
- 輸入: 成本 = [[15, 96], [36, 2]]
- 輸出: 17
- 說明:連結組的最佳方式是:
1--A 2--B This results in a total cost of 17.
範例2:
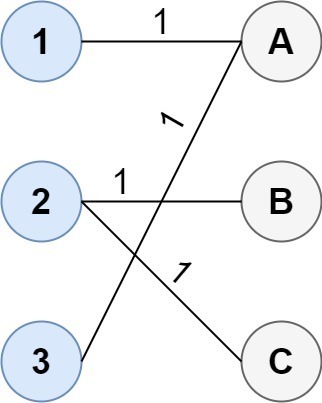
- 輸入: 成本 = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
- 輸出: 4
- 說明:連結組的最佳方式是:
1--A 2--B 2--C 3--A This results in a total cost of 4.
請注意,有多個點連接到第一組中的點 2 和第二組中的點 A。這並不重要,因為可以連接的點數沒有限制。我們只關心最低的總成本。
範例 3:
- 輸入: 成本= [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
- 輸出: 10
約束:
- 大小1 == cost.length
- 大小2 == 成本[i].長度
- 1 1,尺寸2
- 尺寸1>=尺寸2
- 0
提示:
- 左側的每個點要麼連接到已連接到某個左側節點的精確點,要麼連接到右側未連接到任何節點的節點的子集
- 使用帶有位元遮罩的動態規劃,其中狀態將為(第一組中分配的點的數量,第二組中分配的點的位元遮罩)。
解:
我們可以利用具有位元遮罩的動態程式設計。這個想法是透過考慮第一組中的每個點並嘗試將其連接到第二組中的所有點來最小化成本。
具有位元遮罩的動態規劃 (DP) 方法
步驟:
-
國家代表:
- 使用 DP 表 dp[i][mask],其中:
- i 是第一組中的索引(範圍從 0 到 size1-1)。
- mask 是一個位元掩碼,表示第二組中的哪些點已連接。
- 使用 DP 表 dp[i][mask],其中:
-
態轉換:
- 對於第一組中的每個點,請嘗試將其連接到第二組中的每個點,相應地更新 DP 表。
- 如果連接了第二組中的新點,則更新遮罩中的對應位元。
-
基本案例:
- 從 dp[0][0] = 0 開始(最初沒有連接)。
-
目標:
- 計算 dp[size1][(1
讓我們用 PHP 實作這個解:1595。連接兩組點的最低成本
<?php
/**
* @param Integer[][] $cost
* @return Integer
*/
function connectTwoGroups($cost) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$cost1 = [[15, 96], [36, 2]];
$cost2 = [[1, 3, 5], [4, 1, 1], [1, 5, 3]];
$cost3 = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]];
echo connectTwoGroups($cost1) . "\n"; // Output: 17
echo connectTwoGroups($cost2) . "\n"; // Output: 4
echo connectTwoGroups($cost3) . "\n"; // Output: 10
?>
解釋:
- DP 數組 dp[i][mask] 儲存將第 1 組中的前 i 個點與第 2 組中的點連接起來的最小成本,如 mask 所示。
- 巢狀循環迭代 i 和 mask 的每個組合,嘗試透過考慮所有可能的連接來找到最佳成本。
- 最後,解決方案考慮第二組中的某些點可能仍未連接的情況計算最小成本,確保所有點都已連接。
這種方法有效地處理了問題的約束,並確保連接兩組的成本最小。
聯絡連結
如果您發現本系列有幫助,請考慮在 GitHub 上給 存儲庫 一個星號或在您最喜歡的社交網絡上分享該帖子? 。您的支持對我來說意義重大!
如果您想要更多類似的有用內容,請隨時關注我:
- 領英
- GitHub
以上是連接兩組點的最低成本的詳細內容。更多資訊請關注PHP中文網其他相關文章!
陳述:
本文內容由網友自願投稿,版權歸原作者所有。本站不承擔相應的法律責任。如發現涉嫌抄襲或侵權的內容,請聯絡admin@php.cn

