Java 中的排序演算法

依照一定的順序對資訊進行排序，通常是在類似陣列的框架內，就是對它們進行排列。您可以使用不同的順序要求；流行的方法是將數字從小到大排序，反之亦然，或者按字典順序對字串排序。如果您對排序的工作原理感興趣，我們將介紹不同的演算法，從無效但直觀的替代方案到用 Java 和其他語言有效實現的高效演算法。

java不同的排序演算法

有不同的排序演算法，但並非所有演算法都同樣有效。為了比較它們並看看哪些表現最好，我們將分析它們的時間複雜度。

廣告 該類別中的熱門課程 JAVA 掌握 - 專業化 | 78 課程系列 | 15 次模擬測驗

1. 插入排序
2. 冒泡排序
3. 選擇排序
4. 合併排序
5. 堆排序

1.插入排序

插入排序背後的概念將範圍劃分為已排序和未排序的子數組。分類部分位於持續時間 1 的開始處，並與陣列中的第一個（左側）元件相符。我們遍歷數組，並在每次迭代期間將數組的分類部分擴展一個分量。當我們擴展時，我們將新元素放置在已排序的子數組中。為此，我們將所有元素向右移動，直到發現不必更改第一個組件。當粗體部分按升序排序時，例如在下面的陣列中，會出現：

1. 3 5 7 8 4 2 1 9 6：考慮 4 並插入這就是我們需要的。我們從 8 > 開始就一直在轉移。 4
2. 2. 3 5 7 x 8 2 1 9 6
3. 3 5 x 7 8 2 1 9 6
4. 3 x 5 7 8 2 1 9 6
5. 3 4 5 7 8 2 1 9 6

代碼：

public class InsertionSortEx {
public static void insertionSort(int[] arr) {
for (int x = 1; x < arr.length; x++) {
int current = arr[x];
int y = x - 1;
while(y >= 0 && current < arr[y]) {
arr[y+1] = arr[y];
y--;
}
arr[y+1] = current;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,7,8,4,2,1,9,6};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

輸出：

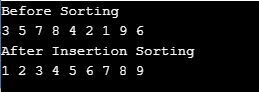
按照這個方法，一個元件擴展了排序後的部分；我們現在有五個而不是四個元素。每次迭代都會執行此操作，整個數組將按末尾排序。

注意：這是因為我們需要在每次迭代中將整個分類清單一一傳輸，時間複雜度為 O(n)。我們必須對每個表中的每個元件執行此操作，這意味著它是 O(n^2) 有界的。 2。

2.冒泡排序

如果氣泡不符合要求的順序，它會透過更換相鄰組件來運作。重複此操作，直到所有元件從陣列的開頭開始按順序排列。我們知道，如果我們設法在不進行交換的情況下完成整個迭代，則與相鄰元素相比的所有項目都處於所需的順序，並且通過擴展，整個數組也處於所需的順序。冒泡排序演算法的原因是像「冒泡」這樣的數字進入「地面」。如果在特定數量之後，您再次瀏覽該實例（4 是一個很好的實例），您會注意到數字慢慢向右移動。

冒泡排序的步驟如下：

1. 4 21 5 3：這裡，1^st 兩個數字的順序不正確；因此我們必須對這兩個數字進行排序。
2. 2 4 15 3：之後，下一對數字的順序也不正確。所以排序再次發生。
3. 2 1 4 53：這兩個順序正確，4
3 5，因此無需交換它們。
4. 2 1 4 5 3
：同樣，我們必須交換正確的順序。
2 1 4 3 5：這是一個迭代後的結果陣列。
我們必須再次重複這個過程，直到數字排列正確。

代碼：

public class BubbleSortExample {
public static void bubbleSort(int[] arr) {
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++){
for(int y=1; y < (n-x); y++){
if(arr[y-1] > arr[y]){
//swap elements
tmp = arr[y-1];
arr[y-1] = arr[y];
arr[y] = tmp;
}
}
}
}
public static void main(String[] args) {
int arr[] ={4,2,1,5,3};
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
}
}

輸出：

注意：

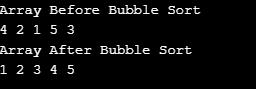
如果我使用a[i]>= a[i+1 ]，它可能會陷入無限循環，因為該連接對於等效組件仍然有效，因此始終將它們從一個組件交換元素到另一個。

3.選擇排序

選擇排序將陣列分割為未排序的分類數組。然而，這一次，排序子數組是透過交換在已排序數組的末尾插入未排序子數組的最小元素而形成的：

1. 3 5 1
2 4
2. 15 3 2
 4
3. 1 23
 5 4
4. 1 2 35 4
5. 1 2 3 45
6. 1 2 3 4 5

代碼：

public class SelectionSortEx {
public static void selectionSort(int[] arr){
for (int x = 0; x < arr.length - 1; x++)
{
int indx = x;
for (int y = x + 1; y < arr.length; y++){
if (arr[y] < arr[indx]){
indx = y;
}
}
int smallNumber = arr[indx];
arr[indx] = arr[x];
arr[x] = smallNumber;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,1,2,4};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

輸出：

<🎜> Note: The minimum is O(n) for the array size because all the components must be checked. For each element of the array, we must find the minimum and make the whole process O (n^2) limited.

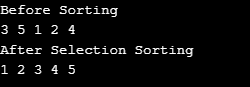
4. Merge Sort

Merge Sort utilizes recursion to fix the issue of the divide and conquest method more effectively than earlier described algorithms.

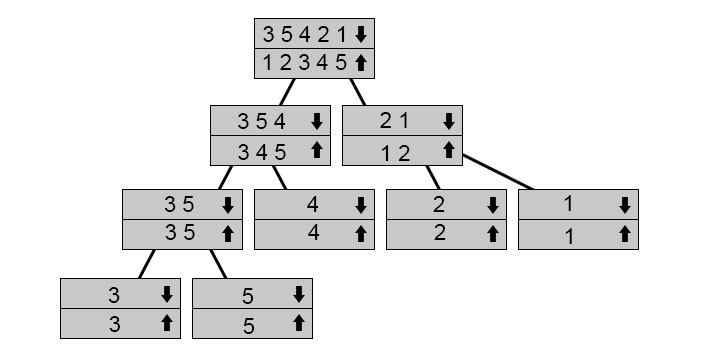
This tree shows how the recursive calls function. Down arrow marked arrays are the arrays for which we call function while we fuse up arrow arrays. Then you follow the arrow to the tree’s edge and then return and merge. We’ve got 3 5 3 1 range, so we split it into 3 5 4 and 2 1. We split them into their parts in order to sort them. We begin fusioning and sorting them as we go when we get to the bottom.

Code:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort {
static void merge(int[] array,int lowval,int midval,int highval){
int x, y ,k;
int[] c= new int[highval-lowval+1];
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval){
if(array[x]<=array[y]){
c[k++] = array[x++];
}
else{
c[k++] = array[y++];
}
}
while(x<=midval){
c[k++] = array[x++];
}
while(y<=highval){
c[k++] = array[y++];
}
k=0;
for(x = lowval; x<=highval; x++){
array[x] = c[k++];
}
}
static void mergeSort(int[] array,int lowval, int highval){
if(highval-lowval+1>1){
int midval = (lowval+highval)/2;
mergeSort(array,lowval,midval);
mergeSort(array,midval+1,highval);
merge(array,lowval,midval,highval);
}
}
public static void main(String[] args) {
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try {
size = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("Please Enter valid Input");
return;
}
int[] array = new int[size];
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) {
try {
array[x] = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("An error Occurred");
}
}
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array,0,array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
}
}

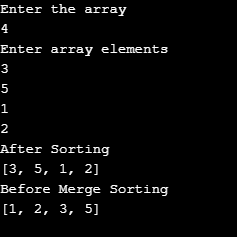
In this program, we have asked the user to enter input. The output will be in sorted order based on the user’s input.

Output:

5. Heap Sort

You first must know the framework on which Heapsort operates-the heap-in order to comprehend why it operates. We will specifically speak about a binary heap, but you can also generalize this to other heap constructions. A heap is a tree that fulfills the property of the heap, namely that all its kids have relationships to each node. A heap must also be nearly finished. A near-complete d-depth binary has a d-1 subtree with the same root, and each node has a full, left subtree, with a left descending.

In other words, you get a lower and lower number (min-heap) or larger and bigger (max-heap) when moving down the tree. Here is a max-heap instance:

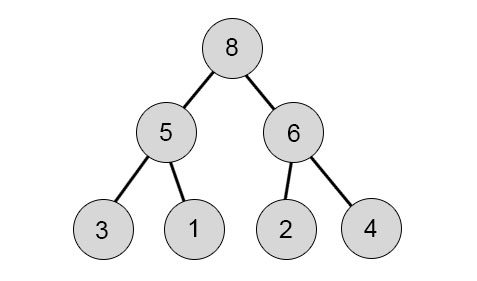
1. 6 1 8 3 5 2 4: Here, Both children’s numbers are smaller than the parent; hence we do not have to change anything.
2. 6 1 8 3 52 4: Here, 5 > 1, we need to swap them. We need to heapify for 5.
3. 6 5 8 3 12 4: Both of the children’s numbers are smaller; everything remains the same.
4. 6 5 83 1 2 4: Here, 8 > 6, hence we should swap them.
5. 8 5 6 3 1 2 4: After this iteration, we will get this result.

After Repeating this process again, we will get the following results:

• 8 5 6 3 1 2 4
1. 4 5 6 3 1 2 8: Swapping
2. 6 5 4 3 1 2 8: Heapify
3. 2 5 4 3 1 6 8: Swapping
4. 5 2 4 2 1 6 8: Heapify
5. 1 2 4 2 5 6 8: Swapping

Code:

public class HeapSort
{
public void sort(int arr[])
{
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr[0];
arr[0] = arr[x];
arr[x] = tmp;
heapify(arr, x, 0);
}
}
void heapify(int arr[], int n, int x)
{
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L < n && arr[L] > arr[largest])
largest = L;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != x)
{
int swap = arr[x];
arr[x] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int x=0; x<n; ++x)
System.out.print(arr[x]+" ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = {6,1,8,3,5,2,4};
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
}
}

Output:



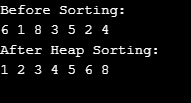
You can view it from point to level of the graph, from left to right. We achieved here that when we have the kth component in the array, the position of its children is 2\*k+1 and 2\*k+2 (assuming that indexing begins at 0). You can monitor this. The position of the parent is always (k-1)/2 for the kth component. You can readily “max heap up” any range because you know that. Check whether one of its kids is lower than that for each component. If so, pair one parent and repeat this step recursively with the parent.

Note: Since iterating for-loops across the entire array makes heapSort) (obviously O(N), it would create Heapsort O’s overall complexity(nlog n). Heapsort has an on-the-spot type, which means that it requires O(1) more room than Merge Sort, but it has some disadvantages, such as parallels that are hard.

Conclusion – Sorting Algorithms in Java

Sorting is a very prevalent procedure with datasets, whether for further analysis, speeding search with more effective algorithms relying on sorted information, filtering information, etc. Several languages endorse sorting, and often the interfaces obscure what the programmer does.

以上是Java 中的排序演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！