具有最大機率的路徑
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB原創
- 2024-08-28 06:40:37768瀏覽
1514。具有最大機率的路徑
難度:中
主題:陣列、圖、堆疊(優先權佇列)、最短路徑
給你一個由n 個節點(0 索引)組成的無向加權圖,由邊列表表示,其中edges[i] = [a, b] 是連接節點a 和b 的無向邊,有成功的機率遍歷該邊succProb[i].
給定兩個節點的起點和終點,找到從起點到終點成功機率最大的路徑,並返回其成功機率。
如果沒有從起點到終點的路徑,返回0。如果您的答案與正確答案相差最多 1e-5.
,我們將接受您的答案。範例1:
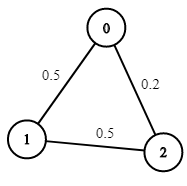
- 輸入: n = 3,edges = [[0,1],[1,2],[0,2]],succProb = [0.5,0.5,0.2],start = 0,end = 2
- 輸出: 0.25000
- 說明:從開始到結束有兩條路徑,一條成功機率 = 0.2,另一條成功機率 0.5 * 0.5 = 0.25。
範例2:
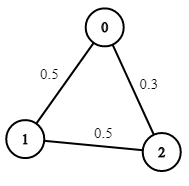
- 輸入: n = 3,edges = [[0,1],[1,2],[0,2]],succProb = [0.5,0.5,0.3],start = 0,end = 2
- 輸出: 0.30000
範例 3:
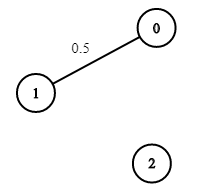
- 輸入: n = 3,edges = [[0,1]],succProb = [0.5],start = 0,end = 2
- 輸出: 0.00000
- 解釋: 0 和 2 之間沒有路徑。
約束:
- 2
- 0
- 開始! =結束
- 0
- a != b
- 0
- 0
- 每兩個節點之間最多有一條邊
提示:
- 機率相乘會導致精度誤差。
- 採用對數機率對數字進行求和而不是相乘。
- 使用 Dijkstra 演算法求否定所有成本後兩個節點之間的最小路徑。
解:
我們可以使用 Dijkstra 演算法的修改版本。您將最大化成功的可能性,而不是尋找最短路徑。
讓我們用 PHP 實作這個解:1514。機率最大的路徑
<?php
/**
* @param Integer $n
* @param Integer[][] $edges
* @param Float[] $succProb
* @param Integer $start_node
* @param Integer $end_node
* @return Float
*/
function maxProbability($n, $edges, $succProb, $start_node, $end_node) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$n1 = 3;
$edges1 = [[0,1],[1,2],[0,2]];
$succProb1 = [0.5,0.5,0.2];
$start_node1 = 0;
$end_node1 = 2;
echo maxProbability($n1, $edges1, $succProb1, $start_node1, $end_node1);//Output: 0.25000
$n2 = 3;
$edges2 = [[0,1],[1,2],[0,2]];
$succProb2 = [0.5,0.5,0.3];
$start_node2 = 0;
$end_node2 = 2;
echo maxProbability($n2, $edges2, $succProb2, $start_node2, $end_node2);//Output: 0.30000
$n3 = 3;
$edges3 = [[0,1]];
$succProb3 = [0.5;
$start_node3 = 0;
$end_node3 = 2;
echo maxProbability($n3, $edges3, $succProb3, $start_node3, $end_node3); //Output: 0.00000
?>
解釋:
圖表示:圖表示為鄰接列表,其中每個節點都指向其鄰居以及連接它們的邊的成功機率。
最大機率數組:陣列maxProb用於儲存起始節點到達每個節點的最大機率。
優先權佇列:最大堆(SplPriorityQueue)用於首先探索機率最高的路徑。這對於確保當我們到達目標節點時,找到機率最大的路徑至關重要。
-
演算法:
- 將起始節點的機率初始化為1(因為停留在起始點的機率為1)。
- 使用優先權佇列來探索節點,更新到達每個鄰居的最大機率。
- 如果到達目的節點,則傳回機率。
- 如果不存在路徑,則回傳0。
輸出:
對於提供的範例:
$n = 3; $edges = [[0,1],[1,2],[0,2]]; $succProb = [0.5,0.5,0.2]; $start_node = 0; $end_node = 2;
輸出將為 0.25。
這種方法確保了使用 Dijkstra 演算法的有效解決方案,同時處理機率計算的細節。
聯絡連結
如果您發現本系列有幫助,請考慮在 GitHub 上給 存儲庫 一個星號或在您最喜歡的社交網絡上分享該帖子? 。您的支持對我來說意義重大!
如果您想要更多類似的有用內容,請隨時關注我:
- 領英
- GitHub
以上是具有最大機率的路徑的詳細內容。更多資訊請關注PHP中文網其他相關文章!
陳述:
本文內容由網友自願投稿,版權歸原作者所有。本站不承擔相應的法律責任。如發現涉嫌抄襲或侵權的內容,請聯絡admin@php.cn

