案例研究：連通圓問題

連通圓問題是判斷二維平面內的所有圓是否連通。這個問題可以使用深度優先遍歷來解決。 DFS演算法有很多應用。本節應用DFS演算法來解決連通圓問題。

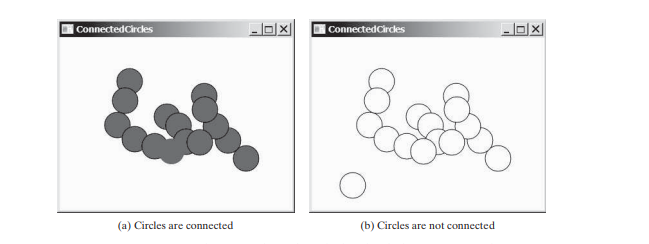
在連通圓問題中，您需要確定二維平面中的所有圓是否都是連通的。如果所有圓都相連，則將它們繪製為實心圓，如下圖（a）所示。否則，它們不會被填充，如下圖(b)所示。

我們將編寫一個程序，讓使用者透過在目前未被圓圈覆蓋的空白區域中點擊滑鼠來建立一個圓圈。當您新增圓圈時，如果圓圈已連接，則會重新繪製填充，否則未填充。

我們將建立一個圖表來模擬問題。每個圓都是圖中的一個頂點。如果兩個圓重疊，則它們是相連的。我們在圖中應用 DFS，如果在深度優先搜尋中找到所有頂點，則圖是連通的。

程式在下面的程式碼中給出。

import javafx.application.Application;
import javafx.geometry.Point2D;
import javafx.scene.Node;
import javafx.scene.Scene;
import javafx.scene.layout.Pane;
import javafx.scene.paint.Color;
import javafx.scene.shape.Circle;
import javafx.stage.Stage;

public class ConnectedCircles extends Application {
    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        // Create a scene and place it in the stage
        Scene scene = new Scene(new CirclePane(), 450, 350);
        primaryStage.setTitle("ConnectedCircles"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Pane for displaying circles */
    class CirclePane extends Pane {
        public CirclePane() {
            this.setOnMouseClicked(e -> {
                if (!isInsideACircle(new Point2D(e.getX(), e.getY()))) {
                    // Add a new circle
                    getChildren().add(new Circle(e.getX(), e.getY(), 20));
                    colorIfConnected();
                }
            });
        }

        /** Returns true if the point is inside an existing circle */
        private boolean isInsideACircle(Point2D p) {
            for (Node circle: this.getChildren())
                if (circle.contains(p))
                    return true;

            return false;
        }

        /** Color all circles if they are connected */
        private void colorIfConnected() {
            if (getChildren().size() == 0)
                return; // No circles in the pane

            // Build the edges
            java.util.List<AbstractGraph.Edge> edges = new java.util.ArrayList<>();
            for (int i = 0; i < getChildren().size(); i++)
                for (int j = i + 1; j < getChildren().size(); j++)
                    if (overlaps((Circle)(getChildren().get(i)), (Circle)(getChildren().get(j)))) {
                        edges.add(new AbstractGraph.Edge(i, j));
                        edges.add(new AbstractGraph.Edge(j, i));
                    }

            // Create a graph with circles as vertices
            Graph<Node> graph = new UnweightedGraph<>((java.util.List<Node>)getChildren(), edges);
            AbstractGraph<Node>.Tree tree = graph.dfs(0); // a DFS tree
            boolean isAllCirclesConnected = getChildren().size() == tree.getNumberOfVerticesFound();

            for (Node circle: getChildren()) {
                if (isAllCirclesConnected) { // All circles are connected
                    ((Circle)circle).setFill(Color.RED);
                }
                else {
                    ((Circle)circle).setStroke(Color.BLACK);
                    ((Circle)circle).setFill(Color.WHITE);
                }
            }
        }
    }

    public static boolean overlaps(Circle circle1, Circle circle2) {
        return new Point2D(circle1.getCenterX(), circle1.getCenterY()).distance(circle2.getCenterX(), circle2.getCenterY()) <= circle1.getRadius() + circle2.getRadius();
    }
}

JavaFX Circle 類別包含資料欄位 x、y 和 radius，它們指定圓的中心位置和半徑。它也定義了 contains 用於測試點是否在圓中。 overlaps 方法（第 76-80 行）檢查兩個圓是否重疊。

當使用者在任何現有圓圈之外按一下滑鼠時，將以滑鼠點為中心建立一個新圓圈，並將該圓圈新增至窗格中（第 26 行）。

為了偵測圓是否相連，程式建構了一個圖（第 46-59 行）。圓圈是圖的頂點。邊緣在第 49-55 行中建構。如果兩個圓頂點重疊，則它們是相連的（第 51 行）。此圖的 DFS 會產生一棵樹（第 60 行）。樹的 getNumberOfVerticesFound() 傳回搜尋到的頂點數。如果它等於圓的數量，則所有圓都相連（第 61-62 行）。

以上是案例研究：連通圓問題的詳細內容。更多資訊請關注PHP中文網其他相關文章！