克服困難：賭場利潤背後的數學

您有沒有想過為什麼賭場似乎總是贏錢？在「克服困難：賭場利潤背後的數學」中，我們將探索確保賭場長期盈利的簡單數學和巧妙策略。透過易於理解的範例和蒙特卡洛模擬，我們將揭示房子邊緣背後的秘密。準備好探索賭場如何扭轉局面！

了解莊家優勢

賭場優勢是賭場世界的基本概念。它代表賭場期望從玩家每次下注中獲得的平均利潤。本質上，它是賭場長期保留的每筆賭注的百分比。

賭場優勢的存在是因為賭場不根據遊戲的「真實賠率」支付獲勝賭注。真實賠率代表事件發生的實際機率。透過以略低的賠率支付，賭場可以確保他們隨著時間的推移賺取利潤。

賭場優勢 (HE) 定義為賭場利潤，以玩家原始賭注的百分比表示。

** 歐式輪盤 ** 只有一個綠色零，總共有 37 個數字。如果玩家在紅色下注 1 美元，他們有 18/37 的機會贏得 1 美元，有 19/37 的機會輸掉 1 美元。期望值為：

預期值=( 1 × 18/37 )+( −1 × 19/37 )= 18/37 − 19/37 = −1/37 = − −2.7%

因此，在歐式輪盤賭中，賭場優勢 (HE) 約為 2.7%。

讓我們自己製作一個遊戲來更好地理解它，一個簡單的擲骰子遊戲。

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll <= 50:
        print(roll, 'You rolled between 1 and 50 and lost.')
        return False
    else:
        print(roll, 'You rolled between 51 and 99 and won! Keep playing!')
        return True

在這個遊戲中：

• 如果擲骰值為 100，則玩家有 1/100 的幾率失敗。

• 如果擲骰結果在 1 到 50 之間，玩家有 50/100 的幾率失敗。

• 如果擲骰結果在 51 到 99 之間，玩家有 49/100 的獲勝機會。

期望值 =(1× 49/100) + ( −1× 51/100) = 49/100 − 51/100 = −2/100 ≈ −2%

因此，賭場優勢為2%。

了解蒙特卡羅模擬

蒙特卡羅模擬是一種強大的工具，用於透過對過程進行大量模擬並觀察結果來理解和預測複雜系統。在賭場的背景下，蒙地卡羅模擬可以對各種投注場景進行建模，以顯示賭場優勢如何確保長期獲利能力。讓我們探索蒙特卡羅模擬的工作原理以及如何將它們應用於簡單的賭場遊戲。

什麼是蒙特卡羅模擬？

蒙特卡羅模擬涉及產生隨機變數來多次模擬過程並分析結果。透過執行數千甚至數百萬次迭代，我們可以獲得可能結果的分佈，並深入了解不同事件發生的可能性。

將蒙特卡羅模擬應用於擲骰子遊戲

我們將使用蒙特卡羅模擬來模擬我們之前討論的擲骰子遊戲。這將幫助我們了解賭場優勢如何隨著時間的推移影響遊戲的獲利能力。

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins += 1
        else:
            losses += 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

解釋結果

在這個模擬中，我們運行骰子遊戲 10,000,000 次來觀察輸贏百分比。鑑於先前計算的賭場優勢 (2%)，我們預計輸錢百分比將略高於贏錢百分比。

運行模擬後，您可能會看到以下結果：

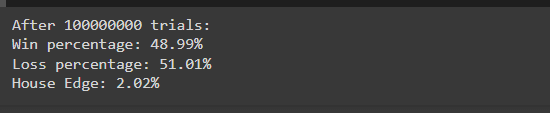
這些結果與理論機率密切相關（49% 獲勝，51% 失敗），展示了賭場優勢在大量試驗中的表現。輕微的不平衡保證了賭場的長期獲利能力。

可視化短期勝利和長期損失

蒙特卡羅模擬對於透過重複隨機抽樣來建模和預測結果非常有用。在賭博的背景下，我們可以使用蒙特卡羅模擬來了解不同投注策略的潛在結果。

我們將模擬一個投注者在每一輪中都下了相同的初始賭注，並觀察他們的帳戶價值在指定的賭注數量上如何變化。

以下是我們如何使用 Matplotlib 模擬和視覺化投注流程：

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager <= wager_count:
        if roll_dice():
            value += wager
        else:
            value -= wager

        wX.append(current_wager)
        vY.append(value)
        current_wager += 1

    return wX, vY

# Parameters for simulation
funds = 10000
initial_wager = 100
wager_count = 1000

# Run the simulation for a single bettor
wager_counts, account_values = bettor_simulation(funds, initial_wager, wager_count)

# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(wager_counts, account_values, label='Bettor 1', color='blue')
plt.xlabel('Wager Count')
plt.ylabel('Account Value')
plt.title('Betting Journey: Short-Term Wins vs Long-Term Losses')
plt.grid(True)
plt.legend()

# Highlighting the short-term and long-term trend
plt.axhline(y=funds, color='gray', linestyle='--', label='Initial Funds')
plt.axhline(y=account_values[0], color='green', linestyle='--', label='Starting Account Value')
plt.axhline(y=account_values[-1], color='red', linestyle='--', label='Final Account Value')

plt.legend()
plt.show()

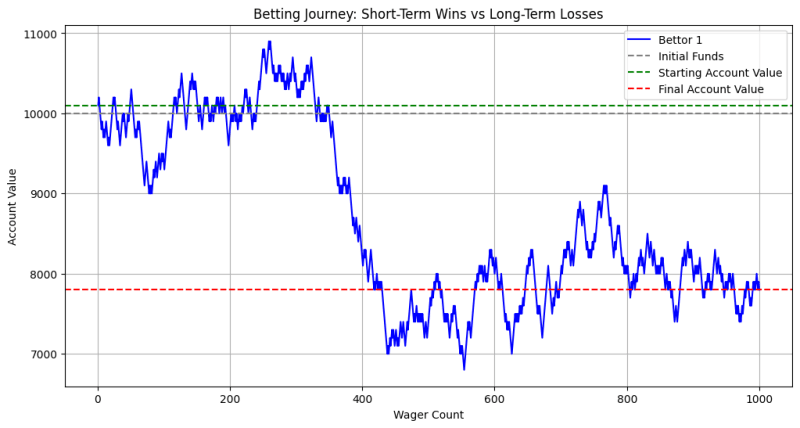
此圖說明了投注者的帳戶價值如何因輸贏而隨時間波動。最初，可能會有一段獲勝的時期（綠線高於起始值），但隨著投注次數的增加，賭場優勢的累積效應變得明顯。最終，投注者的帳戶價值往往會下降到接近或低於初始資金（灰線），表明長期損失。

結論

了解賭場利潤背後的數學原理，可以透過賭場優勢的概念揭示賭場在每場遊戲中的明顯優勢。儘管偶爾會獲勝，但賭場遊戲中內建的機率確保大多數玩家隨著時間的推移會輸錢。蒙特卡羅模擬生動地說明了這些動態，表明由於賭場的統計優勢，即使是短期勝利也可以掩蓋長期損失。這種對賭場獲利能力數學確定性的洞察強調了明智決策和負責任賭博實踐的重要性。

接下來，我們可以探索其他視覺化或變化，例如比較不同的投注策略或分析不同的初始投注對投注者結果的影響。

保持聯繫：

• GitHub：ezhillragesh

• 推特：ezhillragesh

• 網址：ragesh.me

請隨時分享您的想法、提出問題並參與討論。

編碼愉快！

以上是克服困難：賭場利潤背後的數學的詳細內容。更多資訊請關注PHP中文網其他相關文章！