使用回溯法解決八皇后問題

八皇后問題是找到一個解決方案，在棋盤的每一行放置一個皇后，使得兩個皇后不能互相攻擊。該問題可以使用遞歸來解決。在本節中，我們將介紹一種常見的演算法設計技術，稱為回溯來解決這個問題。回溯方法逐步搜尋候選解決方案，一旦確定
就放棄該選項 候選方案不可能是有效的解決方案，然後尋找新的候選方案。

可以使用二維陣列來表示棋盤。然而，由於每一行只能有一個皇后，因此使用一維數組來表示皇后在該行中的位置就足夠了。因此，您可以將 queens 陣列定義為：

int[] queens = new int[8];

將 j 分配給 queens[i] 表示皇后放置在行 i 和列 j 中。下圖(a)顯示了下圖(b)中棋盤的queens陣列的內容。

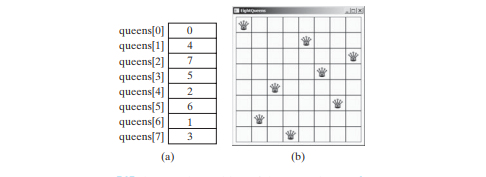
搜尋從第一行開始，其中 k = 0，其中 k 是正在考慮的當前行的索引。此演算法檢查是否可以按 _j = 0, 1, ... , 7 的順序將皇后放置在行中的第 j_ 列中。搜尋實作如下：

• 如果成功，它會繼續在下一行中搜尋皇后的位置。如果當前行是最後一行，則找到解決方案。
• 如果不成功，則回溯到上一行並繼續在上一行的下一列中搜尋新的展示位置。
• 如果演算法回溯到第一行並且無法在該行中找到皇后的新位置，則無法找到解決方案。

下面的程式碼給出了顯示八皇后問題解決方案的程式。

package application;
import javafx.application.Application;
import javafx.geometry.Pos;
import javafx.stage.Stage;
import javafx.scene.Scene;
import javafx.scene.control.Label;
import javafx.scene.image.Image;
import javafx.scene.image.ImageView;
import javafx.scene.layout.GridPane;

public class EightQueens extends Application {
    public static final int SIZE = 8; // The size of the chess board
    // queens are placed at (i, queens[i])
    // -1 indicates that no queen is currently placed in the ith row
    // Initially, place a queen at (0, 0) in the 0th row
    private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1};

    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        search(); // Search for a solution

        // Display chess board
        GridPane chessBoard = new GridPane();
        chessBoard.setAlignment(Pos.CENTER);
        Label[][] labels = new Label[SIZE][SIZE];
        for(int i = 0; i < SIZE; i++)
            for(int j = 0; j < SIZE; j++) {
                chessBoard.add(labels[i][j] = new Label(), i, j);
                labels[i][j].setStyle("-fx-border-color: black");
                labels[i][j].setPrefSize(55, 55);
            }

        // Display queens
        Image image = new Image("file:C:/Users/Paul/development/MyJavaFX/src/application/image/lo.jpg");
        for(int i = 0; i < SIZE; i++)
            labels[i][queens[i]].setGraphic(new ImageView(image));

        // Create a scene and place it in the stage
        Scene scene = new Scene(chessBoard, 55 * SIZE, 55 * SIZE);
        primaryStage.setTitle("EightQueens"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Search for a solution */
    private boolean search() {
        // k - 1 indicates the number of queens placed so far
        // We are looking for a position in the kth row to place a queen
        int k = 0;
        while(k >= 0 && k < SIZE) {
            // Find a position to place a queen in the kth row
            int j = findPosition(k);
            if(j < 0) {
                queens[k] = -1;
                k--; // back track to the previous row
            } else {
                queens[k] = j;
                k++;
            }
        }

        if(k == -1)
            return false; // No solution
        else
            return true; // A solution is found
    }

    public int findPosition(int k) {
        int start = queens[k] + 1; // Search for a new placement

        for(int j =start; j < SIZE; j++) {
            if(isValid(k, j))
                return j; // (k, j) is the place to put the queen now
        }

        return -1;
    }

    /** Return true is a queen can be placed at (row, column) */
    public boolean isValid(int row, int column) {
        for(int i = 1; i <= row; i++)
            if(queens[row - i] == column // Check column
            || queens[row - i] == column - i // Check upleft diagonal
            || queens[row - i] == column + i) // Check upright diagonal
                return false; // There is a conflict
        return true; // No conflict
    }

}

程式呼叫search()（第20行）來搜尋解決方案。最初，任何行中都沒有放置皇后（第 16 行）。現在，搜尋從第一行 k = 0（第 53 行）開始，並找到皇后的位置（第 56 行）。如果成功，請將其放入該行（第 61 行）並考慮下一行（第 62 行）。如果不成功，則回溯到上一行（第 58-59 行）。

findPosition(k) 方法從queen[k] + 1 開始搜尋在行k 放置皇后的可能位置（第73 行） ） 。它檢查是否可以將皇后放置在 start, start + 1, 。 。 。 、和 7，依此順序（第 75-78 行）。如果可能，傳回列索引（第77行）；否則，傳回 -1（第 80 行）。

呼叫isValid(row, column)方法來檢查在指定位置放置皇后是否會與先前放置的皇后發生衝突（第76行）。它確保沒有皇后被放置在同一列（第86行）、左上角對角線（第87行）或右上角對角線（第88行），如下圖所示。

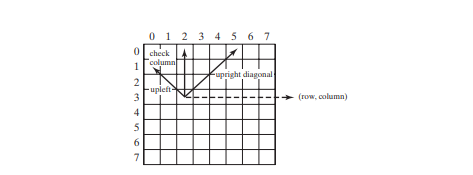
以上是使用回溯法解決八皇后問題的詳細內容。更多資訊請關注PHP中文網其他相關文章！