使用動態規劃尋找斐波那契數

本節分析並設計了一種使用動態規劃來尋找斐波那契數的有效演算法。第18.3節，案例研究：計算斐波那契數，給出了找出斐波那契數的遞歸方法，如下：

/**求斐波那契數列的方法*/
公共靜態長 fib（長索引）{
if (index == 0) // 基本狀況
回傳 0;
else if (index == 1) // 基本狀況
回傳 1;
else // 歸約與遞歸呼叫
返回 fib(索引 - 1) + fib(索引 - 2);
}

我們現在可以證明這個演算法的複雜度是O(2^n)。為了方便起見，設索引為n。令T(n) 表示查找fib(n) 的演算法的複雜度，c 表示將索引與0 和1 進行比較的常數時間；也是說，T(1) 和T(0) 是c。因此，

與漢諾塔問題的分析類似，我們可以證明T(n)是O(2^n)。

但是，這個演算法效率不高。是否有一個有效的演算法來找出斐波那契數？遞歸 fib 方法的問題在於該方法使用相同的參數進行冗餘呼叫。例如，要計算 fib(4)，將呼叫 fib(3) 和 fib(2)。為了計算 fib(3)，需要呼叫 fib(2) 和 fib(1)。請注意，fib(2) 被冗餘調用。我們可以透過避免使用相同參數重複呼叫 fib 方法來改進它。請注意，新的斐波那契數是透過將序列中的前兩個數相加而獲得的。如果使用兩個變數f0 和f1 來儲存前面的兩個數字，則可以透過新增f0 立即取得新數字f2 與f1。現在，您應該透過將f1 分配給f0 並將f2 指派給f1 來更新f0 和f1 來更新f0 和

f1 來更新

f0 和

f1

，如下圖。

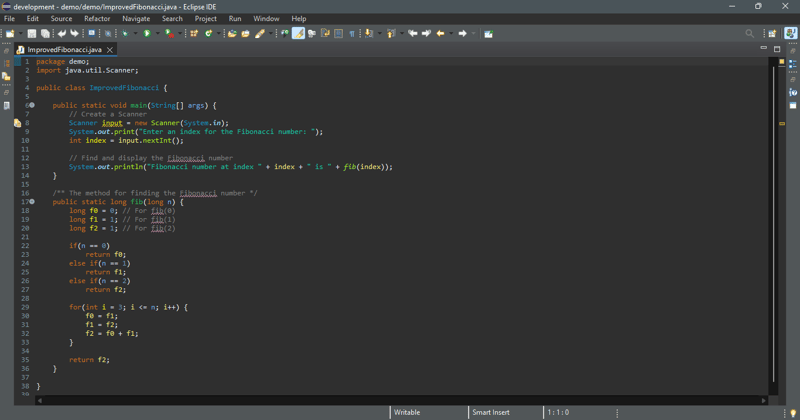
新方法在下面的程式碼中實作。

輸入斐波那契數列的索引：6

索引 6 處的斐波那契數是 8

輸入斐波那契數列的索引：7 索引 7 處的斐波那契數是 13

顯然，這個新演算法的複雜度是O(n)。這是對遞歸 O(2^n) 演算法的巨大改進。 這裡介紹的計算斐波那契數的演算法使用了一種稱為動態規劃的方法。動態規劃是解決子問題，然後組合子問題的解以獲得整體解決方案的過程。這自然會導致遞歸解決方案。然而，使用遞歸效率很低，因為子問題重疊。動態規劃背後的關鍵思想是只解決每個子問題一次，並將子問題的結果儲存起來以供以後使用，以避免子問題的冗餘計算。

以上是使用動態規劃尋找斐波那契數的詳細內容。更多資訊請關注PHP中文網其他相關文章！