
AIxiv專欄是本站發布學術、技術內容的欄位。過去數年,本站AIxiv專欄接收通報了2,000多篇內容,涵蓋全球各大專院校與企業的頂尖實驗室,有效促進了學術交流與傳播。如果您有優秀的工作想要分享,歡迎投稿或聯絡報道。投稿信箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com
在人工智慧領域的發展過程中,對大語言模型(LLM)的控制與指導始終是核心挑戰之一,旨在確保這些模型既強大又安全地服務人類社會。早期的努力集中在透過人類回饋的強化學習方法(RLHF)來管理這些模型,成效顯著,標誌著向更人性化 AI 邁出的關鍵一步。
儘管 RLHF 取得了巨大成功,但在訓練過程中 RLHF 非常消耗資源。因此,近段時間學者們在 RLHF 奠定的堅實基礎上,繼續探索更為簡單且高效的策略優化路徑,催生了直接偏好優化(DPO)的誕生。 DPO 透過數學推理得到獎勵函數與最優策略之間的直接映射,消除了獎勵模型的訓練過程,直接在偏好資料上優化策略模型,實現了從「回饋到策略」的直觀飛躍。這不僅減少了複雜度,也增強了演算法的穩健性,迅速成為業界的新寵。
然而,DPO 主要關注在逆 KL 散度約束下的策略最佳化。由於逆 KL 散度的 mode-seeking 特性,DPO 在提升對齊性能方面表現出色,但這一特性也傾向於在生成過程中減少多樣性,可能限制模型的能力。另一方面,儘管 DPO 從句子級的角度控制 KL 散度,模型的生成過程本質上是逐個 token 進行的。從句子層級控制 KL 散度直觀上顯示 DPO 在細粒度控制上有限制,對 KL 散度的調節能力較弱,可能是 DPO 訓練過程中 LLM 的生成多樣性迅速下降的關鍵因素之一。
為此,來自中科院和倫敦大學學院的汪軍與張海峰團隊提出了一種從 token-level 角度建模的大模型對齊演算法:TDPO。

論文標題:Token-level Direct Preference Optimization
論文地址:https://arxiv.org/abs/2404.1199999303000707070703030g? /Token-level-Direct-Preference-Optimization
為了應對模型產生多樣性顯著下降的問題,TDPO 從token-level 的角度重新定義了整個對齊流程的目標函數,並透過將Bradley-Terry 模型轉換為優勢函數的形式,使得整個對齊流程能最終從Token-level 層級進行分析與最佳化。相較於DPO 而言,TDPO 的主要貢獻如下:
Token-level 的建模方式:TDPO 從Token-level 的角度對問題進行了建模,對RLHF 進行了更精細的分析;
細粒度KL 散度約束:在每個token 處從理論上引入了前向KL 散度約束,使方法能夠更好地約束模型優化;
性能優勢明顯:相比於DPO 而言,TDPO 能夠實現更好的對齊性能和生成多樣性的帕累托前沿。
DPO 與 TDPO 的主要差異如下圖所示:
 DPO 從 sentence-level 的角度進行建模
DPO 從 sentence-level 的角度進行建模
 圖 2:TDPO 的對齊最佳化方式。 TDPO 從token-level 的角度進行建模,並在每個token 處引入了額外的前向KL 散度約束,如圖中紅色部分所示,控制模型偏移程度的同時,充當了模型對齊的baseline
圖 2:TDPO 的對齊最佳化方式。 TDPO 從token-level 的角度進行建模,並在每個token 處引入了額外的前向KL 散度約束,如圖中紅色部分所示,控制模型偏移程度的同時,充當了模型對齊的baseline
下面介紹兩者方法的具體推導過程。
背景:直接偏好優化(DPO)DPO 透過數學推導,得到了獎勵函數與最優策略之間的直接映射,消除了RLHF 過程中的獎勵建模階段:
將公式(1) 代入Bradley-Terry (BT) 偏好模型中,得到直接策略最佳化(DPO)損失函數:
其中 是由來自偏好資料集 D 的 prompt、獲勝回應和失敗回應所構成的偏好對。
是由來自偏好資料集 D 的 prompt、獲勝回應和失敗回應所構成的偏好對。
TDPO
符號標註
為了建模語言模型順序的、自回歸的產生過程,TDPO 將產生回應表示成 T 5 (詞彙表)。 
 當將文本生成建模為馬可夫決策過程時,狀態state 定義為prompt 和到當前step 為止已生成的token 的組合,表示為
當將文本生成建模為馬可夫決策過程時,狀態state 定義為prompt 和到當前step 為止已生成的token 的組合,表示為 ,而動作action 則對應於下一個生成的token,表示為
,而動作action 則對應於下一個生成的token,表示為
。 
 基於上述提供的定義,TDPO 為策略
基於上述提供的定義,TDPO 為策略 建立了狀態 - 動作函數
建立了狀態 - 動作函數
和優勢函數 :
:


其中, 表示折扣因子。
表示折扣因子。
 Token-level 角度的人類回饋強化學習
Token-level 角度的人類回饋強化學習
TDPO 理論上修改了 RLHF 的獎勵建模階段和 RL 微調階段,將它們擴展為了從 token-level 角度考慮的最佳化目標。
對於獎勵建模階段, TDPO 建立了Bradley-Terry 模型和優勢函數之間的相關性:對於RL 微調階段,TDPO 定義了以下目標函數:
從目標(4) 出發,TDPO 在每個token 上推導了最優策略
和狀態- 動作函數 之間的映射關係:
之間的映射關係:
其中, 表示配分函數。
表示配分函數。
將方程式(5) 代入方程式(3),我們得到:

其中, 表示策略模型
表示策略模型 和參考模型
和參考模型 表示的隱式獎勵函數差異,表示為
表示的隱式獎勵函數差異,表示為

表示 和
和 的序列級前向KL 散度差異,按
的序列級前向KL 散度差異,按 加權,表示為
加權,表示為


實際中, 損失傾向於增加
損失傾向於增加 ,放大
,放大 和
和 之間的差異,TDPO 提出修改方程式(9) 為:
之間的差異,TDPO 提出修改方程式(9) 為:

其中 是一個超參數,而
是一個超參數,而

是一個超參數,而
是一個超參數,而
是一個超參數,而
其中
是一個超參數,而其中🎜是一個超參數,而🎜🎜🎜🎜其中🎜是一個超參數,而🎜停止梯度傳播運算子。 🎜🎜我們將TDPO 和DPO 的損失函數總結如下:🎜🎜🎜🎜🎜由此可見,TDPO 在每個token 處引入了這種前向KL 散度控制,使得在優化過程中能夠更好地控制KL的變化,而不影響對齊性能,從而實現了更優的帕累托前緣。 🎜🎜🎜實驗設定🎜🎜🎜TDPO 在 IMDb,Anthropic/hh-rlhf、MT-Bench 上個資料集上進行了實驗。 🎜🎜🎜IMDb🎜🎜
在 IMDb 資料集上,該團隊採用了 GPT-2 作為基底模型,然後以 siebert/sentiment-roberta-large-english 作為獎勵模型評估策略模型輸出,實驗結果如圖 3 所示。

從圖3 (a) 可以看出,TDPO (TDPO1,TDPO2) 能夠達到比DPO 更好的reward-KL 的帕累托前沿,而從圖3 (b)-(d) 則可以看出,TDPO 在KL 散度控制方面表現極為出色,遠優於DPO 演算法的KL 散度控制能力。
Anthropic HH
而在Anthropic/hh-rlhf 資料集上,該團隊採用了Pythia 2.8B 作為基底模型,採用兩種方式評估模型產生的好壞:1)使用現有的指標;2222222 )使用GPT-4 評測。
對於第一種評估方式,該團隊評估了不同演算法訓練的模型在對齊性能 (Accuracy) 和生成多樣性 (Entropy) 上的權衡,如表 1 所示。

可以看到TDPO 演算法不僅在對齊效能(Accuracy) 上優於DPO 和f-DPO,在產生多樣性(Entropy) 上也佔據優勢,在這兩個大模型產生回應的關鍵指標上達到了更好的權衡。
而對於第二種評估方式,該團隊評測了不同演算法訓練的模型和人類偏好的吻合度,與資料集中的獲勝響應作對比,如圖 4 所示。

DPO、TDPO1 和 TDPO2 演算法在溫度係數為 0.75 的情況下均能夠達到對獲勝響應的勝率高於 50%,較好地符合人類偏好。
MT-Bench
在論文中的最後一個實驗上,該團隊採用了在Anthropic HH 資料集上訓練好的Pythia 2.8B 模型直接用於MT-Bench 資料集評測,結果如圖5 所測試示。

在 MT-Bench 上,TDPO 能夠達到比其他演算法更高的獲勝機率,這充分說明了 TDPO 演算法訓練的模型產生的反應的品質更高。
此外,有相關研究對DPO、TDPO、SimPO 演算法進行了對比,可參考連結:https://www.zhihu.com/question/651021172/answer/3513696851
基於eurus 提供的eval 腳本,測了基底模型qwen-4b、mistral-0.1、deepseek-math-base 是基於不同的對齊演算法DPO、TDPO、SimPO 微調訓練所得到的效能,以下是實驗的實驗結果:
 2:DPO, TDPO,SimPO 演算法效能比較
2:DPO, TDPO,SimPO 演算法效能比較
了解更多結果,請參考原論文。
以上是從RLHF到DPO再到TDPO,大模型對齊演算法已經是「token-level」的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM
AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM經常使用“ AI-Ready勞動力”一詞,但是在供應鏈行業中確實意味著什麼? 供應鏈管理協會(ASCM)首席執行官安倍·埃什肯納齊(Abe Eshkenazi)表示,它表示能夠評論家的專業人員
 一家公司如何悄悄地努力改變AIApr 26, 2025 am 11:12 AM
一家公司如何悄悄地努力改變AIApr 26, 2025 am 11:12 AM分散的AI革命正在悄悄地獲得動力。 本週五在德克薩斯州奧斯汀,Bittensor最終遊戲峰會標誌著一個關鍵時刻,將分散的AI(DEAI)從理論轉變為實際應用。 與閃閃發光的廣告不同
 NVIDIA釋放NEMO微服務以簡化AI代理開發Apr 26, 2025 am 11:11 AM
NVIDIA釋放NEMO微服務以簡化AI代理開發Apr 26, 2025 am 11:11 AM企業AI面臨數據集成挑戰 企業AI的應用面臨一項重大挑戰:構建能夠通過持續學習業務數據來保持準確性和實用性的系統。 NeMo微服務通過創建Nvidia所描述的“數據飛輪”來解決這個問題,允許AI系統通過持續接觸企業信息和用戶互動來保持相關性。 這個新推出的工具包包含五個關鍵微服務: NeMo Customizer 處理大型語言模型的微調,具有更高的訓練吞吐量。 NeMo Evaluator 提供針對自定義基準的AI模型簡化評估。 NeMo Guardrails 實施安全控制,以保持合規性和適當的
 AI為藝術與設計的未來描繪了一幅新圖片Apr 26, 2025 am 11:10 AM
AI為藝術與設計的未來描繪了一幅新圖片Apr 26, 2025 am 11:10 AMAI:藝術與設計的未來畫卷 人工智能(AI)正以前所未有的方式改變藝術與設計領域,其影響已不僅限於業餘愛好者,更深刻地波及專業人士。 AI生成的藝術作品和設計方案正在迅速取代傳統的素材圖片和許多交易性設計活動中的設計師,例如廣告、社交媒體圖片生成和網頁設計。 然而,專業藝術家和設計師也發現AI的實用價值。他們將AI作為輔助工具,探索新的美學可能性,融合不同的風格,創造新穎的視覺效果。 AI幫助藝術家和設計師自動化重複性任務,提出不同的設計元素並提供創意輸入。 AI支持風格遷移,即將一種圖像的風格應用
 Zoom如何徹底改變與Agent AI的合作:從會議到里程碑Apr 26, 2025 am 11:09 AM
Zoom如何徹底改變與Agent AI的合作:從會議到里程碑Apr 26, 2025 am 11:09 AMZoom最初以其視頻會議平台而聞名,它通過創新使用Agentic AI來引領工作場所革命。 最近與Zoom的CTO XD黃的對話揭示了該公司雄心勃勃的願景。 定義代理AI 黃d
 對大學的存在威脅Apr 26, 2025 am 11:08 AM
對大學的存在威脅Apr 26, 2025 am 11:08 AMAI會徹底改變教育嗎? 這個問題是促使教育者和利益相關者的認真反思。 AI融入教育既提出了機遇和挑戰。 正如科技Edvocate的馬修·林奇(Matthew Lynch)所指出的那樣
 原型:美國科學家正在國外尋找工作Apr 26, 2025 am 11:07 AM
原型:美國科學家正在國外尋找工作Apr 26, 2025 am 11:07 AM美國科學研究和技術發展或將面臨挑戰,這或許是由於預算削減導致的。據《自然》雜誌報導,2025年1月至3月期間,美國科學家申請海外工作的數量比2024年同期增加了32%。此前一項民意調查顯示,75%的受訪研究人員正在考慮前往歐洲和加拿大尋找工作。 過去幾個月,數百項NIH和NSF的撥款被終止,NIH今年的新撥款減少了約23億美元,下降幅度接近三分之一。洩露的預算提案顯示,特朗普政府正在考慮大幅削減科學機構的預算,削減幅度可能高達50%。 基礎研究領域的動盪也影響了美國的一大優勢:吸引海外人才。 35
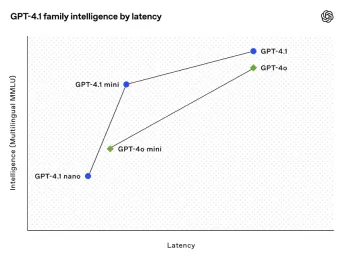 所有有關打開AI最新的GPT 4.1家庭的信息 - 分析VidhyaApr 26, 2025 am 10:19 AM
所有有關打開AI最新的GPT 4.1家庭的信息 - 分析VidhyaApr 26, 2025 am 10:19 AMOpenai推出了強大的GPT-4.1系列:一個專為現實世界應用設計的三種高級語言模型家族。 這種巨大的飛躍提供了更快的響應時間,增強的理解和大幅降低了成本


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

DVWA
Damn Vulnerable Web App (DVWA) 是一個PHP/MySQL的Web應用程序,非常容易受到攻擊。它的主要目標是成為安全專業人員在合法環境中測試自己的技能和工具的輔助工具,幫助Web開發人員更好地理解保護網路應用程式的過程,並幫助教師/學生在課堂環境中教授/學習Web應用程式安全性。 DVWA的目標是透過簡單直接的介面練習一些最常見的Web漏洞,難度各不相同。請注意,該軟體中

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

SecLists
SecLists是最終安全測試人員的伙伴。它是一個包含各種類型清單的集合,這些清單在安全評估過程中經常使用,而且都在一個地方。 SecLists透過方便地提供安全測試人員可能需要的所有列表,幫助提高安全測試的效率和生產力。清單類型包括使用者名稱、密碼、URL、模糊測試有效載荷、敏感資料模式、Web shell等等。測試人員只需將此儲存庫拉到新的測試機上,他就可以存取所需的每種類型的清單。

WebStorm Mac版
好用的JavaScript開發工具





