一、整體架構

#主要任務可分為三類。首先是因果結構的發現,即從資料中辨識出變數之間的因果關係。其次是因果效應的估計,即從資料推斷一個變數對另一個變數的影響程度。需要注意的是,這種影響並非指相對性,而是指在對一個變數進行幹預時,另一個變數的數值或分佈如何變化。最後是校正偏差,因為在許多任務中,各種因素可能導致開發樣本和應用樣本的分佈不同。在這種情況下,因果推論可能有助於我們進行校正偏差。
這些功能適用於多種場景,其中最典型的是決策場景。透過因果推斷,可以了解不同使用者對我們的決策行為的反應。其次,在工業場景中,業務流程通常複雜且長,導致數據偏差。透過因果推論清晰描述這些偏差的因果關係,可以幫助我們進行糾偏。此外,許多場景對模型的穩健性和解釋性要求很高。希望模型能夠基於因果關係進行預測,因果推論可以幫助建立更強大的解釋性模型。最後,決策結果的效果評估也很重要。透過因果推論可以幫助更好地分析策略的實際效果。
接下來將介紹因果推論中的兩個重要問題:如何判斷一個場景是否適合應用因果推斷,以及因果推論中的典型演算法。 首先,判斷一個場景是否適合應用因果推論是十分關鍵的。因果推論通常用於解決因果關係的問題,即透過觀察到的數據來推斷出原因和結果之間的關係。因此,在判斷一個
#二、應用場景評估(決策問題)
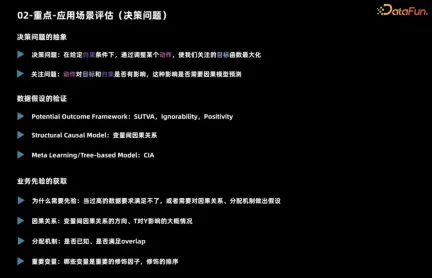
#首先介紹應用場景評估,判斷一個場景是否適合使用推論主要涉及決策問題。
關於一個決策問題,首先需要先明確其是什麼,即在什麼約束條件下做出什麼動作,以達到最大化什麼樣的目標。接著需要考慮這個動作對目標和限制是否產生影響,以及是否需要使用因果推論模型來預測。 舉例來說,在行銷產品時,我們通常會考慮在給定總預算的情況下,決定是否給每個用戶發放優惠券或折扣。以最大化銷售額作為總目標進行考慮。如果沒有預算約束,可能會影響最終的銷售額,但只要知道其是正向策略,就可以給所有用戶打折。 在這種情況下,雖然決策動作對目標有影響,但無需使用因果推論模型進行預測。
以上是決策問題的基本分析,此外還需觀察資料條目是否滿足。對於建構因果模型,不同的因果演算法對資料和任務的假設有不同的要求。
- 潛在結果類別的模型有三個關鍵的假設。首先,個體的因果效應必須是穩定的,例如在探究發優惠券對用戶購買機率的影響時,要確保一個用戶的行為不受其他用戶的影響,例如在線下比價或受到不同折扣版本的優惠券影響。第二個假設是,在給定的特徵情況下,使用者的實際處理和潛在結果是獨立的,這個假設可以用來處理觀測不到的混雜。第三個假設是關於 overlap 的,也就是任何一種使用者都應該給予不同的決策,否則就無法觀察到這種使用者在不同決策下的表現。
- 結構因果類別的模型所面臨的主要假設是變數之間的因果關係,這些假設往往難以證明。而使用 Meta learning 和基於樹的方法時,其假設通常是條件獨立的,即在給定特徵的情況下,決策動作和潛在結果是獨立的。這個假設與前面提到的獨立性假設相似。
在實際業務場景中,了解先驗知識至關重要。首先,需要先理解實際觀測資料的分配機制,也就是先前決策的基礎。當無法獲得最準確的數據時,可能需要依靠一些假設來進行推論。其次,業務經驗可以指導我們確定哪些變數對於區分因果效應具有顯著影響,這對於進行特徵工程至關重要。因此,在處理實際業務時,結合觀測資料的分配機制和業務經驗,能夠更好地應對挑戰,有效地進行決策和特徵工程。
三、典型的因果演算法

第二個重要議題是因果推論演算法的選用。
首先是因果結構發現類別演算法。這些演算法的核心目標是確定變數之間的因果關係。主要的研究思路主要可分為三類。第一類方法是根據因果圖中的節點網路條件獨立性特性進行判斷。另一類方法是定義一個評分函數來衡量因果圖的品質。例如,透過定義似然函數,尋求使得該函數最大化的有向無環圖,並將其作為因果圖。第三類方法則是引入了更多的資訊。例如,假設兩個變數的實際資料產生過程遵循 a n m 型,即加性雜訊模型,然後再求解這兩個變數之間的因果關係方向。
因果效應的估計值涉及多種演算法,以下介紹幾種常見的演算法:
#- 首先是計量經濟學常被提及的工具變數法、did 法和合成控制法。工具變量法的核心思想在於尋找與處理相關但與隨機誤差項無關的變量,即工具變量。此時工具變量與因變量之間的關係不受混雜的影響,可以將預測分為兩個階段:首先利用工具變量預測處理變量,然後利用預測的處理變量來預測因變量,得到的回歸係數即為平均處理效應(ATE)。而 DID 方法和合成控制法則是針對面板資料而設計的方法,但在此不作詳細介紹。
- 另一種常見的方法是利用傾向分數來估計因果效果。這種方法的核心是預測隱藏的分配機制,例如發放優惠券與不發放優惠券的機率。如果兩個用戶具有相同的優惠券發放機率,但實際上一個用戶收到了優惠券,另一個用戶沒有,那麼我們可以認為這兩個用戶在分配機制上是等價的,因此可以比較它們的效果。基於這一點,可以推廣出一系列方法,包括匹配方法、分層方法和加權方法等。
- 還有一個方法是直接預測結果。即存在觀測不到的混雜情況下,也可以透過假設直接預測結果,並透過模型自動進行調整。然而,這種方法可能引發一個問題:如果直接預測結果就足夠,那麼問題就不存在了嗎?實際上,並非如此。
- 第四是結合傾向分數和潛在結果的思路,使用雙重穩健和雙重機器學習的方法可能會更準確。雙重穩健和雙重機器學習將兩種方法結合在一起,其中任何一個部分的準確性都可以確保最終結果的可靠性,從而提供了雙重保障。
- 另一種方法是結構因果類別的模型,基於因果關係建構模型,如因果圖或結構化方程式。這種方法允許直接幹預某個變數以獲得結果,並進行反事實推論。然而,這種方法的前提是我們已經了解變數之間的因果關係,這往往是一個奢侈的假設。
- Meta learning 方法是一種重要的學習方法,其涵蓋了多種不同的類別。其中之一是 S-learning,該方法將處理方法視為一個特徵,直接輸入模型中。透過調整這個特徵,我們可以觀察到不同處理方法下結果的變化。這種方法有時被稱為單一模型學習者,因為我們為實驗組和對照組各建立了一個模型,然後透過修改特徵來觀察結果。另一種方法是 X-learning,其流程類似於 S-learning,但額外考慮了交叉驗證的步驟,以更準確地評估模型的性能。
- 樹狀法是一種直覺且簡單的方法,透過建構樹狀結構來分裂樣本,使得左右節點上的因果效應差異最大化。然而,這種方法容易過度擬合,因此在實務上常常採用隨機森林等方法來減少過度擬合的風險。使用 boosting 方法可能會增加挑戰,因為它更容易過濾掉一些訊息,所以在使用時需要設計更複雜的模型以防止資訊遺失。 Meta learning 方法和基於樹的演算法通常也被稱為 Uplift model。
- 因果表徵是近年來在學術界取得一定成果的領域之一。此方法致力於解耦不同模組,將影響因素分開,以更精確地識別混淆因素。透過分析影響因變數y 和處理變數(treatment)的因素,可以辨識出可能影響 y 和 treatment 的混淆因素,這些因素稱為混淆因素。這種方法有望提高模型的端到端學習效果。以傾向分數為例,它常常在處理混淆因素時表現優異。然而,傾向得分的過度準確有時並非有利。在同一傾向分數下,可能出現無法滿足重疊假設的情況,這是因為傾向分數可能包含一些與混淆因素相關但不影響y 的資訊。當模型學習過於準確時,在加權匹配或分層處理時,可能會導致較大的誤差。這些誤差其實並非由混淆因素所引起,因此並不需要考慮。因果表徵學習方法提供了解決這個問題的途徑,能夠更有效地處理因果關係的識別和分析。
#四、因果推論實際落點中的難點

因果推論在實際應用上面臨諸多挑戰。
- 因果關係的弱化。在許多場景中,因果關係往往與隨機波動的噪音處於同一量級,這給建模工作帶來了巨大的挑戰。在這種情況下,建模的收益相對較低,因為因果關係本身並不明顯。然而,即使必須進行建模,也需要採用具有更強學習能力的模型才能夠準確地捕捉到這種弱化的因果關係。同時,需要特別注意過擬合的問題,因為學習能力較強的模型可能會更容易受到雜訊的影響,導致模型過度擬合資料。
- 第二個普遍存在的問題是資料條件的不足。這個問題的範圍較為廣泛,主要原因在於我們所使用的演算法假設存在許多不足之處,特別是在利用觀測資料進行建模時,我們的假設可能並不完全成立。其中最典型的問題包括重疊假設可能無法滿足,我們的分配機制可能缺乏隨機性。更嚴重的問題是,我們甚至沒有足夠的隨機測試數據,這使得我們難以客觀地評估模型的表現。在這種情況下,如果仍然堅持進行建模,而且模型效能優於同比規則,那麼我們可以藉助一些業務經驗來評估模型的決策是否合理。從業務角度出發,對於一些假設不成立的情況,例如未觀測到的混雜因素,從理論上並沒有特別好的解決方法,但如果一定要使用模型,可以嘗試根據業務經驗或進行一些小規模的隨機測試來評估混雜因素的影響方向和程度。同時,將這些因素考慮到模型中,對於不滿足重疊假設的情況,雖然這在我們後面的列舉中作為第四個問題,但在此一併討論,我們可以通過一些算法來排除一些分配機制中的非混雜因素,即透過因果表示學習來緩解此問題。
- 在處理這種複雜性時,決策動作顯得格外重要。許多現有模型主要專注於解決二元問題,然而,若涉及多個處理方案,如何分配資源便成為一個更為複雜的問題。針對這項挑戰,我們可以將多個處理方案分解成不同領域的子問題。此外,利用深度學習方法,我們可以將處理方案視為特徵,並假設連續處理方案與結果之間存在某種函數關係。透過優化這些函數的參數,可以更好地解決連續決策問題,然而,這也引入了一些額外的假設,例如重疊問題。
- 分配機制固定。見上述分析。
- 另一個常見問題是目標預測很多。在某些情況下,目標預測受到多種因素的影響,而這些因素又與處理方案相關聯。為了解決這個問題,我們可以採用多任務學習的方法,儘管直接處理複雜的角色問題可能較為困難,但我們可以透過簡化問題,僅預測受處理方案影響最為關鍵的指標,逐步為決策提供參考。
- 最後,在某些場景下進行隨機測試的成本較高,效果回收週期較長。在模型上線之前,充分評估模型的效果變得特別重要。在這種情況下,進行小規模的隨機測試可以用來評估效果。儘管評估模型所需的樣本集比建模樣本集少得多,但如果甚至無法進行小規模的隨機測試,那麼我們可能只能透過業務解釋性來判斷模型決策結果的合理性。
#五、個案-京東科技的額度決策模式
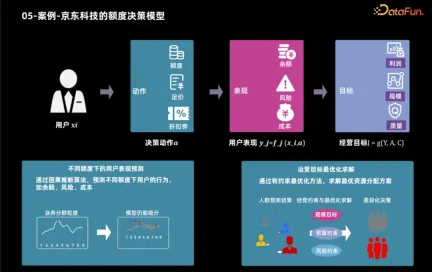
接下來以京東科技利用因果推論技術制定信貸產品的輔助應用為例,展示如何根據使用者特徵和經營目標確定最佳信貸額度。在確定經營目標後,這些目標通常可以細分為使用者表現的指標,如使用者的產品使用情況和借款行為。透過分析這些指標,可以計算出利潤、規模等經營目標。因此,額度決策過程分為兩個步驟:首先利用因果推論技術預測使用者在不同額度下的表現,然後根據這些表現和經營目標,採用各種方法來確定每個使用者的最佳信用額度。
#
六、未來發展

在未來的發展中將面對一系列挑戰與機會。
首先,針對當前因果模型存在的不足之處,學界普遍認為需要大規模的模型來處理更複雜的非線性關係。因果模型通常只處理二維數據,大多數模型結構相對簡單,因此未來的研究方向可能包括解決這個問題。
其次,研究者提出了因果表示學習的概念,強調了解耦和模組化思想在表示學習中的重要性。透過從因果關係的角度來理解資料生成過程,基於真實世界規律建構的模型很可能具有更好的遷移能力和泛化性。
最後,研究者指出當前的假設過於強大,許多情況下難以滿足實際需求,因此需要針對不同情境採用不同的模型。這也導致了模型落地的門檻相當高。因此,尋找通用性強的萬金油演算法具有巨大的價值。
以上是劃重點! !因果推斷兩大演算法框架解析的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 特斯拉自动驾驶算法和模型解读Apr 11, 2023 pm 12:04 PM
特斯拉自动驾驶算法和模型解读Apr 11, 2023 pm 12:04 PM特斯拉是一个典型的AI公司,过去一年训练了75000个神经网络,意味着每8分钟就要出一个新的模型,共有281个模型用到了特斯拉的车上。接下来我们分几个方面来解读特斯拉FSD的算法和模型进展。01 感知 Occupancy Network特斯拉今年在感知方面的一个重点技术是Occupancy Network (占据网络)。研究机器人技术的同学肯定对occupancy grid不会陌生,occupancy表示空间中每个3D体素(voxel)是否被占据,可以是0/1二元表示,也可以是[0, 1]之间的
 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
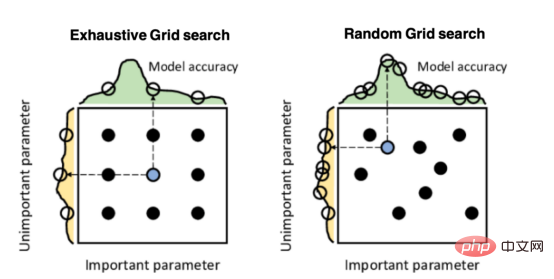
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
 因果推断主要技术思想与方法总结Apr 12, 2023 am 08:10 AM
因果推断主要技术思想与方法总结Apr 12, 2023 am 08:10 AM导读:因果推断是数据科学的一个重要分支,在互联网和工业界的产品迭代、算法和激励策略的评估中都扮演者重要的角色,结合数据、实验或者统计计量模型来计算新的改变带来的收益,是决策制定的基础。然而,因果推断并不是一件简单的事情。首先,在日常生活中,人们常常把相关和因果混为一谈。相关往往代表着两个变量具有同时增长或者降低的趋势,但是因果意味着我们想要知道对一个变量施加改变的时候会发生什么样的结果,或者说我们期望得到反事实的结果,如果过去做了不一样的动作,未来是否会发生改变?然而难点在于,反事实的数据往往是
 使用Pytorch实现对比学习SimCLR 进行自监督预训练Apr 10, 2023 pm 02:11 PM
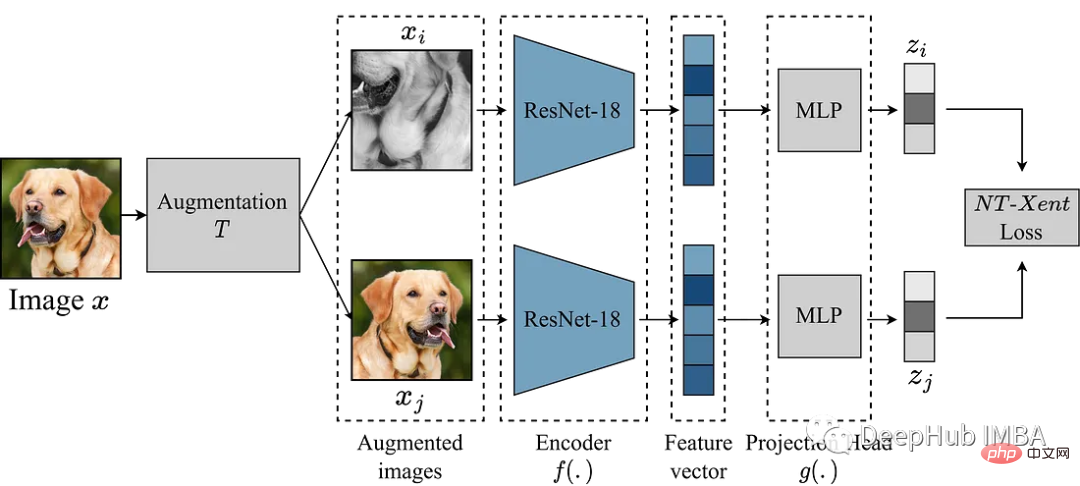
使用Pytorch实现对比学习SimCLR 进行自监督预训练Apr 10, 2023 pm 02:11 PMSimCLR(Simple Framework for Contrastive Learning of Representations)是一种学习图像表示的自监督技术。 与传统的监督学习方法不同,SimCLR 不依赖标记数据来学习有用的表示。 它利用对比学习框架来学习一组有用的特征,这些特征可以从未标记的图像中捕获高级语义信息。SimCLR 已被证明在各种图像分类基准上优于最先进的无监督学习方法。 并且它学习到的表示可以很容易地转移到下游任务,例如对象检测、语义分割和小样本学习,只需在较小的标记
 盒马供应链算法实战Apr 10, 2023 pm 09:11 PM
盒马供应链算法实战Apr 10, 2023 pm 09:11 PM一、盒马供应链介绍1、盒马商业模式盒马是一个技术创新的公司,更是一个消费驱动的公司,回归消费者价值:买的到、买的好、买的方便、买的放心、买的开心。盒马包含盒马鲜生、X 会员店、盒马超云、盒马邻里等多种业务模式,其中最核心的商业模式是线上线下一体化,最快 30 分钟到家的 O2O(即盒马鲜生)模式。2、盒马经营品类介绍盒马精选全球品质商品,追求极致新鲜;结合品类特点和消费者购物体验预期,为不同品类选择最为高效的经营模式。盒马生鲜的销售占比达 60%~70%,是最核心的品类,该品类的特点是用户预期时
 人类反超 AI:DeepMind 用 AI 打破矩阵乘法计算速度 50 年记录一周后,数学家再次刷新Apr 11, 2023 pm 01:16 PM
人类反超 AI:DeepMind 用 AI 打破矩阵乘法计算速度 50 年记录一周后,数学家再次刷新Apr 11, 2023 pm 01:16 PM10 月 5 日,AlphaTensor 横空出世,DeepMind 宣布其解决了数学领域 50 年来一个悬而未决的数学算法问题,即矩阵乘法。AlphaTensor 成为首个用于为矩阵乘法等数学问题发现新颖、高效且可证明正确的算法的 AI 系统。论文《Discovering faster matrix multiplication algorithms with reinforcement learning》也登上了 Nature 封面。然而,AlphaTensor 的记录仅保持了一周,便被人类
 机器学习必知必会十大算法!Apr 12, 2023 am 09:34 AM
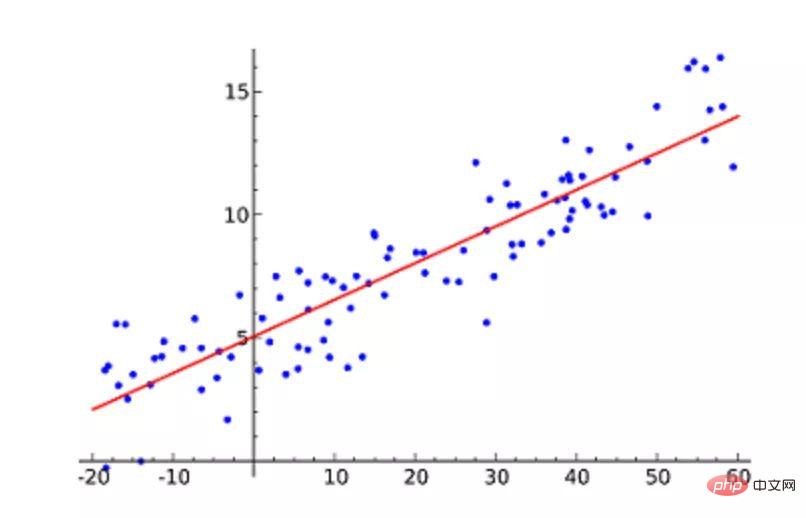
机器学习必知必会十大算法!Apr 12, 2023 am 09:34 AM1.线性回归线性回归(Linear Regression)可能是最流行的机器学习算法。线性回归就是要找一条直线,并且让这条直线尽可能地拟合散点图中的数据点。它试图通过将直线方程与该数据拟合来表示自变量(x 值)和数值结果(y 值)。然后就可以用这条线来预测未来的值!这种算法最常用的技术是最小二乘法(Least of squares)。这个方法计算出最佳拟合线,以使得与直线上每个数据点的垂直距离最小。总距离是所有数据点的垂直距离(绿线)的平方和。其思想是通过最小化这个平方误差或距离来拟合模型。例如


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

禪工作室 13.0.1
強大的PHP整合開發環境

SublimeText3漢化版
中文版,非常好用

SublimeText3 Linux新版
SublimeText3 Linux最新版

記事本++7.3.1
好用且免費的程式碼編輯器

Dreamweaver CS6
視覺化網頁開發工具






