碰到了一个关于元组的算法问题
请大家帮忙看看,能不能给个答案,或者解决思路也行.
谢谢!
三元组(a,b,c)标识a币种到b币种的汇率为c,反向亦成立。
输入一堆这样的三元组,再指定两个币种x y,问x->y的汇率是多少?
请编程实现,并给出时间、空间复杂度。
注意:x->y的汇率是唯一的。
怪我咯2017-04-18 10:24:18
Idea: Triplet -> Directed graph -> Find the path of any two nodes -> Matrix multiplication or Floyd-Warshal.
For example, the foreign exchange price obtained is:
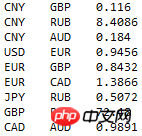
The first line indicates that every 1 yuan can be exchanged for 0.116 pounds. Each triple (c1, c2, r)对应两条带权重的边:c1 -> c2 weighted r和c2 -> c1 weighted 1/r. These quotes actually give a directed graph:
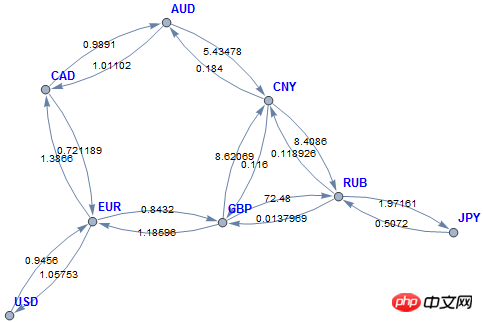
It is assumed here that the given triplet will not lead to contradictions, and the directed graph is connected (there will be no failure to convert). This directed graph is written as a weighted adjacency matrix:
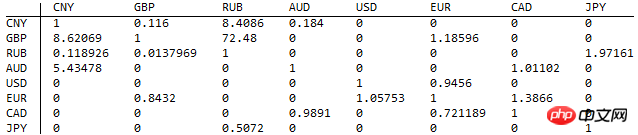
Matrix elementA[i,j]表示1单位i币种可以兑换多少单位的jCurrency. Zeros in the matrix represent that the current exchange rate is unknown.
Place the matrixA连乘可以逐步去除这些零元素。但是要把普通矩阵相乘中计算点积的加法替换成“取第一个大于零的数,若没有则为零”的操作。例如:(1,2,3).(0,3,2) = first_positive(1*0, 2*3, 3*2) = 6.
Calculate with “Exchange Rate Multiplication”A的乘方,A^k表示最多经过k-1步折算得到的汇率表,一直算到A^k中没有零停止。如果有n种货币,最多计算到A^(n-1).
A^3: 
Observe the first line of A^3的第一行,它是所有货币对人民币的比价。任两种货币的比价就是把它们对人民币的比价的商。所以其实一开始用A的第一行参加计算就好:A[1] * A * ... * A (最多n-1次), it is the price comparison of all currencies against the RMB. The comparison of any two currencies is the quotient of their comparison with the RMB. So in fact, just use the first line of A to participate in the calculation: A[1] * A * ... * A (up to n-1 times), each time The multiplication of row vectors and matrices is performed until all elements of the row are non-zero. The complexity of this calculation is O(n³).
Adjust the recursion relationship in the shortest path algorithmFloyd-Warshal, which can also be used for exchange rate conversion in this question. The complexity of Floyd-Warshal is Θ(n³). So matrix multiplication might be faster.
for k from 1 to rows(A)
for i from 1 to rows(A)
for j from 1 to rows(A)
if A[i][j] = 0 then
// 货币 i, j 通过货币 k 折算
A[i][j] <- A[i][k] * A[k][j]
end ifBoth algorithms need to store the exchange rate matrix, so the space complexity is Θ(n²).
高洛峰2017-04-18 10:24:18
If an array of triples is provided, generate an optimal solution for calculating the x->y exchange rate: directed graph shortest path algorithm
If you provide a different triple array each time, you only need to get one result: directed graph pathfinding algorithm
巴扎黑2017-04-18 10:24:18
Tuples can be used as keys of dict
>>> ls = [('人民币', '美元'), ('人民币', '欧元'), ('人民币', '英镑')]
>>> 汇率表 = dict(zip(ls,(6.,7.,8.)))
{('人民币', '美元'): 6.0, ('人民币', '英镑'): 8.0, ('人民币', '欧元'): 7.0}
>>> import pprint
>>> pprint.pprint(汇率表,width=10)
{('人民币', '欧元'): 7.0,
('人民币', '美元'): 6.0,
('人民币', '英镑'): 8.0}
>>> 汇率表[('人民币', '美元')]
6.0黄舟2017-04-18 10:24:18
Some of the algorithms above are very complicated to write. Let’s write a simple one:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>
typedef struct node{
char *str; /*拼接后的字符串*/
float value; /*汇率值*/
}node_t;
int main(int argc, char *argv[])
{
/*用户输入的一序列汇率对应关系*/
static char const *buff[] = {"CNY","GBP","0.116",\
"CNY","RUB","8.406",\
"CNY","AUD","0.184",\
"JPY","RUB","0.5072",\
"USD","EUR", "0.9456"};
int npairs = sizeof(buff)/sizeof(buff[0])/3;
node_t * buf = calloc(1,npairs*sizeof(node_t));
if(NULL == buf){
printf("calloc is null !\n");
return(-1);
}
int i = 0;
int j = 0;
int len = 0;
char tmp[16] = {'[field@learn]$./test_hello
please input the two node:
CNY GBP
CNY->GBP 0.116000
[field@learn]$./test_hello
please input the two node:
GBP CNY
CNY->GBP 0.116000
[field@learn]$
'};
for(i=0;i<npairs*3; i+= 3){
memset(tmp,'rrreee',sizeof(tmp));
/*把两个字符串进行拼接*/
snprintf(tmp,16,"%s%s",buff[i],buff[i+1]);
len = strlen(tmp);
buf[j].str = calloc(1,sizeof(char)*(len+1));
if(NULL != buf[j].str){
memmove(buf[j].str,tmp,len);
buf[j].value = atof(buff[i+2]);
j += 1;
}
}
printf("please input the two node:\n");
char input0[8] = {'rrreee'};
char input1[8] = {'rrreee'};
scanf("%s%s",input0,input1);
char data0[16] = {'rrreee'};
char data1[16] = {'rrreee'};
/*考虑正序和反序*/
snprintf(data0,16,"%s%s",input0,input1);
snprintf(data1,16,"%s%s",input1,input0);
for(i=0;i<j;++i){
/*轮训匹配*/
if((0==strcmp(buf[i].str,data0))){
printf("%s->%s %f \n",input0,input1,buf[i].value);
break;
}
if( 0==strcmp(buf[i].str,data1) ){
printf("%s->%s %f \n",input1,input0,buf[i].value);
break;
}
}
if(i==j){
printf("can not find the pair \n");
}
/*
add the free
*/
return 0;
}The test results are as follows:
rrreeeWhat is used here is the uniqueness of the currency name. The two currencies spliced together must be unique.