c++ - 李白打酒有什么解法

Question

李白打酒

话说大诗人李白，一生好饮。幸好他从不开车。
一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：
无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。

这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。 
请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。
注意：通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。

我想到过暴力枚举，但是效果似乎不是很好。这个题用DFS算法解决是很好，但是不理解递归的使用。而且回溯的时候，也不知道这样能不能跑完所有情况。在此求助。

Answer 1

The answer to this question using recursion is 14:

1. bababaababbbbbb

2. babaabbabbabbbb

3. babaababbbbbabb

4. baabbaabbabbbb

5. baabbabbbaabbbb

6. baabbabbabbbabb

7. baababbbbbababb

8. abbbabaabbabbbb

9. abbbaabbbaabbbb

10. abbaabbabbbabb

11. abbabbbabaabbbb

12. abbabbbaabbbabb

13. abbabbabbbababb

14. ababbbbbabababb

In addition to forward recursion, reverse recursion is also possible:

• Forward: Starting from (花,店,酒) = (0,0,2), recursively ending at (10,5,0).

• Reverse: Work backwards from (10,5,0), (10,5,0) -> (9,5,1) -> (8,5,2)... until the end of (0,0,2).

Try to deduce two or three steps by hand and you will find that the backward method may be better. Because only when the amount of alcohol is an even number, we need to consider using the store to halve the amount of alcohol . In every step of the forward push method, two situations, the flower and the store, must be considered. Actual implementation also found that the backward inference method is significantly better than the forward inference method.

The picture below is the call tree of the backward method. The number in the circle is the amount of alcohol after each step of inference, the letters on the arrow P(ub)=hotel, F(lowe)r=flower. The red path is the sequence that meets the requirements. There are 149 recursive calls in total (intermediate results are cached, and calls with the same form are only counted once).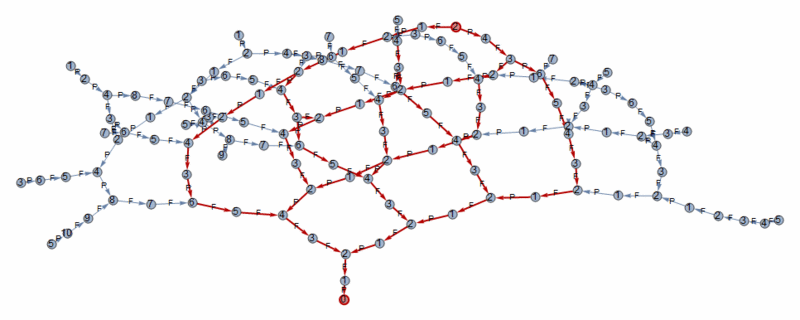

The picture below is the forward push method call tree, and the logo is omitted. There are a total of 1051 recursive calls, most of which are doing useless work.

Answer 2

#include <cstdio>

int count=0;

void dfs(int a, int b, int wine) {
//    printf("%d %d %d\n",a, b, wine);
    if(!a && !b && wine == 1) count++;
    else {
        b--; wine--;
        if(a >= 0 && b >= 0 && wine >= 1)
            dfs(a, b, wine);
        
        b++; wine++;
        
        
        a--; wine *= 2;
        if(a >= 0 && b >= 0 && wine >= 1)
            dfs(a, b, wine);
        
        a++; wine /= 2;
    }
}

int main() {
    int a=5, b=9, wine=2;
    
    dfs(a, b, wine);
    
    printf("%d\n",count);
    return 0;
} 

The last time we met flowers, we just finished drinking the wine, so we fixed the last b, and the problem was simplified to the conditional arrangement of 5 a and 9 b, and finally there was 1 bucket of wine left.
There are only two situations in the question. When b-1, wine-1, dfs enters the next level to check whether a=0, b=0 and wine=1 are met; when a-1, the same is true;
It should be noted that after b-1, wine-1, and dfs enter the next layer, the values ​​​​of b and wine must be changed back, otherwise it will affect the execution of the following statements.

Answer 3

We used recursion back then.

Anyway, it’s a fill-in-the-blank question.

Answer 4

Can be solved using a subset of binary enumerations.

int ans = 0;
for (int i = 0; i < (1<<14); ++i) {
    int tot_1 = 0;
    int tot_0 = 0;
    int num = 2;
    for (int j = 0; j < 14; ++j) {
        if (i&(1 << j)) { // 这里判断二进制 i 从右数第 j + 1位是否为1
            tot_1++;
            num = num*2;
        } else {
            tot_0++;
            num = num - 1;
        }
    }
    if (tot_1 == 5 && tot_0 == 9 && num == 1) {
        ++ans; //记录合法方案书
    }
}

The above solution is excerpted from the Blue Bridge Cup course on Jisuanke. I am not a sailor, but an ordinary student of Jisuanke. I saw the gmail sf push and then encountered this problem. Therefore, I will answer the question. If you are going to the Blue Bridge Cup, you might as well consider the course offered by Jiaji Garanke. It has a lot of questions and is also taught by teachers who are among the 27 finalists in the world. The link above is a promotional link. After registration, both parties will get coupons... .