Question 1:
"When we assign a value to an unsigned type that exceeds its representation range, the result is the remainder of the initial value modulo the total number of values represented by the unsigned type." How do you understand this sentence? For example, why is the result of assigning -1 to an 8-bit unsigned char 255?
My understanding is this: If -1=11111111 (the first 1 represents negative), when it is expressed as unsigned, 11111111=255
Then why is assigning a signed type a value beyond its representation range? When the value of the result is undefined?
Question 2
When both signed and unsigned types appear in an arithmetic expression, when the value of the signed type is a positive number, is the value after conversion to unsigned the same as before conversion? For example, int a=1, unsigned b=1, when outputting a b, a will be converted to unsigned first. Will a be equal to 1 after conversion? If int a=-1, unsingned b=2, when outputting a b, a will be converted to an unsigned type first. What is the value of a after conversion?
Question 2: 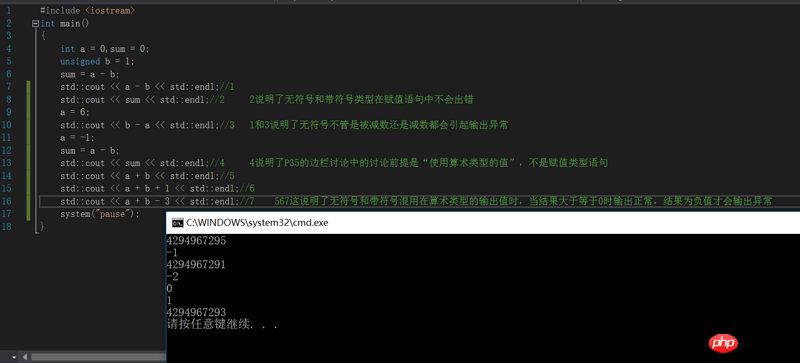
The fourth long comment is shown in the picture.
What the book says is that no matter what the result of a b is, as long as a and b are unsigned and the other is signed, the signed one must be converted to unsigned before the addition is performed. After I actually ran the program in the picture, I thought that only when the result of a b is a negative number and a and b are signed and unsigned, the result is converted to unsigned.
Which one is right?
巴扎黑2017-06-19 09:09:29
Question 1
In fact, the explanation above is complicated. If you look at it from the perspective of memory, you will find that it is very simple. The difference between unsigned and signed is not the storage of memory, but the acquisition of memory. For example, in your example of assigning 8 bits to -1, if it is unsigned, only the last 8 binary bits will be filled, and the rest will be discarded. Because this 8bit is unsigned, all the binary bits in it represent numbers, so it is 255. But if it is a signed 8-bit, the first binary bit represents the sign bit, but when assigning, the sign bit of -1 does not become the sign bit of the 8-bit data, so the sign bit of the 8-bit data is actually invalid, so this assignment is error. That sentence means (-1)%256=255, where 256 is the total number of unsigned 8bits (or range).
Question 2
As mentioned above, in fact, the storage methods of signed and unsigned are the same, but the reading methods are different. The signed one will treat the first bit as the sign bit, and the unsigned one will treat the first bit as the numeric bit. It's the same in memory. In your example, the result of the first time a + b is a bunch of 1's in binary representation. If you output directly, since it is converted to unsigned, that is, two unsigned are added, the result is unsigned, and the binary output of a bunch of 1's as unsigned is 4294967295, but if a+b is assigned to sum, sum stores the value. There are still a bunch of 1's in the memory, but since sum is a signed int, when reading, the first bit is regarded as the sign bit, so the read value is -1.
So in your question 2, it is not that there is no conversion during operation, but because only binary is considered when storing values, and there is no difference whether there is a sign or not. The sign bit is only judged when reading, which leads to differences in output results.