I encountered a written test question and had no idea at all. Please ask for help. . . .
The known classes are defined as follows
class Node {
public Double value;
public List<Node> children;
}The input node meets the following conditions:
1 The value of node is a floating point number greater than 0
2 The value of node's subordinate nodes (and lower-level nodes) may be null or a floating point number greater than 0
The function of the program is as follows:
1 Set all null values in the tree structure to floating point numbers greater than 0
2 The value of non-leaf nodes (that is, nodes with a number of children greater than 0) is equal to its children The sum of values
public void doit(Node node){
......
}Example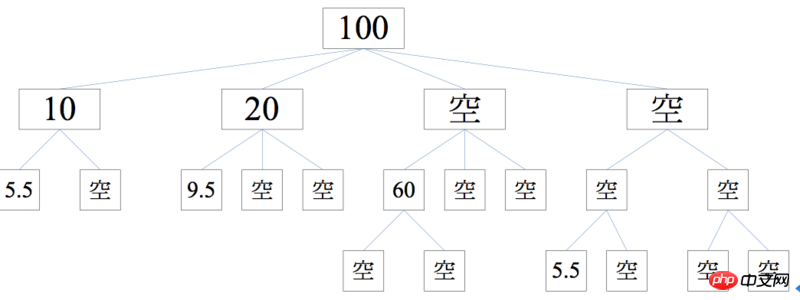
Answer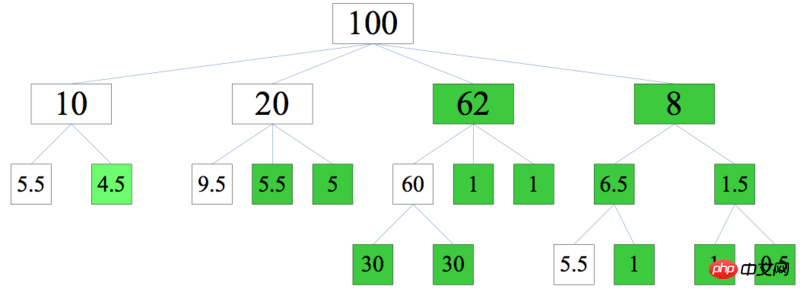
How to answer this question?
Some experts have already answered it. Combining the answers of the two people below is the perfect answer. In fact, if I adopt the answer and change the equal distribution to random, it will be perfect
淡淡烟草味2017-05-27 17:41:30
I haven’t written any specific code, but let’s talk about the idea
First, divide the problem into 2 steps
Step1. Determine the value of the non-leaf node
Step2. Determine the value of the leaf node
Process Step1 first. After Step1 is processed, there is no need for Step2. As I said, just divide it equally according to the value of the parent node.
For Step1,
step1-1: Traverse each non-leaf node from bottom to top, and determine its minimum value by summing its child nodes. For example, the rightmost subtree has a minimum value of 5.5.
step1-2: From top to bottom, determine the non-leaf nodes layer by layer, which are aspect descriptions. Name [100] as the first layer, [10, 20, ?, ?] as the second layer, and so on. According to the result of step1-1, the minimum value of the second layer is [10, 20, >60, >5.5]. Subtract the sum of the minimum values from 100, and then divide it equally. The result is [10, 20, 62.25, 7.75]
step1-3: Same as above, determine the third layer, the result is [5.5, 4.5] [9.5, 5.25, 5.25] [60, 1.125, 1.125] [6.625, 1.125]
The last group here is more special and needs to be considered By the time 7.75 is allocated, there is already 5.5 in the lower left corner, so the freely available number in 7.75 is 7.75-5.5=2.25. Divide 2.25 equally to both sides, and the result is [6.625, 1.125]
step1-4: The last layer believes No need to be wordy, it’s actually step 2, just divide it equally.
伊谢尔伦2017-05-27 17:41:30
I just read this question and found it very interesting. Then I thought about it and asked the following questions.
My idea is recursion.
Traverse hierarchically, add up the determined values at each level, and divide the empty nodes into the value of the parent node minus the sum of the determined values (requirements of the question). Then if the node is not a leaf node, recurse according to the above method.
But when determining the value of each node, such as certain leaf nodes, we need to assign values to them randomly. Some of their values are constrained by the parent node, and some are not constrained by the parent node, such as the third node on the second layer. The two leaf nodes of , if the values we assign to them make their parent nodes do not meet the requirements, this does not meet the meaning of the question. So what I want is to pass in the value range of these nodes every time the value is determined. The determination of these scopes will lead to some problems, and the problems will become complicated.
The range is determined. The maximum value of each empty node must be the sum of the value of the parent node minus the value of the same child node. The minimum value must be greater than the sum of valuable elements of its child nodes. Because only a certain range is determined, the selection of some random values of its leaf nodes will not cause the remaining nodes to not meet the meaning of the question. Generally speaking, the values of each empty node with the same parent node are mutually constrained. Although the value of one node satisfies itself, it will make the other nodes not meet the requirements. For example: 
If the value is taken in this way, it will be locally satisfied, which will cause the values of other nodes not to meet the requirements. Therefore, it may lead to unexpected results without constraints. We need to determine these ranges.
To sum up, these are just some of my thoughts after thinking about it. There may be some mistakes and please correct me.