- masyarakat
- Belajar
- Perpustakaan Alatan
- Masa lapang
Rumah > Soal Jawab > teks badan
碰到了一个关于元组的算法问题
请大家帮忙看看,能不能给个答案,或者解决思路也行.
谢谢!
三元组(a,b,c)标识a币种到b币种的汇率为c,反向亦成立。
输入一堆这样的三元组,再指定两个币种x y,问x->y的汇率是多少?
请编程实现,并给出时间、空间复杂度。
注意:x->y的汇率是唯一的。
怪我咯2017-04-18 10:24:18
Idea: Triplet -> Graf terarah ->
Sebagai contoh, harga tukaran mata wang asing yang diperolehi ialah:
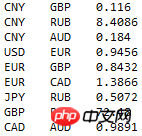
Baris pertama menunjukkan bahawa setiap 1 yuan boleh ditukar dengan 0.116 paun. Setiap tiga kali ganda (c1, c2, r) sepadan dengan dua tepi berwajaran: c1 -> c2 weighted r dan c2 -> c1 weighted 1/r. Petikan ini sebenarnya memberikan graf terarah:
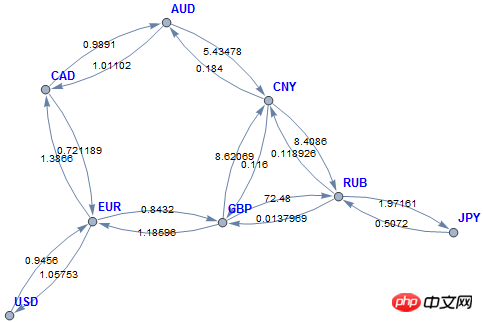
Adalah diandaikan di sini bahawa triplet yang diberikan tidak akan membawa kepada percanggahan, dan graf yang diarahkan disambungkan (tidak akan ada ketidakfahaman). Graf terarah ini ditulis sebagai matriks bersebelahan berwajaran:
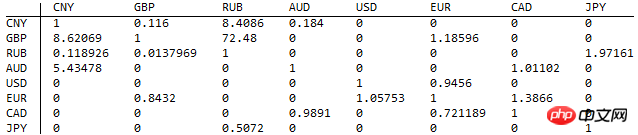
Elemen matriks A[i,j] mewakili berapa banyak unit i mata wang boleh ditukar dengan 1 unit j mata wang. Sifar dalam matriks menunjukkan bahawa kadar pertukaran semasa tidak diketahui.
Mendarab matriks A boleh mengeluarkan unsur sifar ini secara beransur-ansur. Tetapi penambahan mengira hasil darab titik dalam pendaraban matriks biasa perlu digantikan dengan operasi "dapatkan nombor pertama lebih besar daripada sifar, atau sifar jika tidak". Contohnya: (1,2,3).(0,3,2) = first_positive(1*0, 2*3, 3*2) = 6.
Gunakan "Pendaraban Kadar Pertukaran" untuk mengira kuasa A A^k mewakili jadual kadar pertukaran yang ditukar paling banyak k-1 langkah, dan pengiraan diteruskan sehingga tiada sifar dalam A^k. Jika terdapat n mata wang, sehingga A^(n-1) akan dikira.
A^3: 
Perhatikan baris pertama A^3, ia adalah perbandingan harga semua mata wang berbanding RMB. Perbandingan mana-mana dua mata wang adalah hasil bagi perbandingan mereka dengan RMB. Jadi sebenarnya, hanya gunakan baris pertama A untuk mengambil bahagian dalam pengiraan pada permulaan: A[1] * A * ... * A (最多n-1次), setiap kali vektor baris dan matriks didarab sehingga semua elemen baris itu bukan sifar. Kerumitan pengiraan ini ialah O(n³).
Laraskan perhubungan rekursi dalam algoritma laluan terpendek Floyd-Warshal dan ia juga boleh digunakan untuk penukaran kadar pertukaran dalam soalan ini. Kerumitan Floyd-Warshal ialah Θ(n³). Jadi pendaraban matriks mungkin lebih cepat.
for k from 1 to rows(A)
for i from 1 to rows(A)
for j from 1 to rows(A)
if A[i][j] = 0 then
// 货币 i, j 通过货币 k 折算
A[i][j] <- A[i][k] * A[k][j]
end ifKedua-dua algoritma perlu menyimpan matriks kadar pertukaran, jadi kerumitan ruang ialah Θ(n²).
高洛峰2017-04-18 10:24:18
Jika tatasusunan tiga kali ganda disediakan, hasilkan penyelesaian optimum untuk mengira kadar pertukaran x->y: Algoritma Laluan Terpendek Graf Berarah
Jika anda menyediakan tatasusunan tiga kali ganda yang berbeza setiap kali, anda hanya perlu mendapatkan satu hasil: algoritma pencarian laluan graf terarah
巴扎黑2017-04-18 10:24:18
Tuple boleh digunakan sebagai kunci dict
>>> ls = [('人民币', '美元'), ('人民币', '欧元'), ('人民币', '英镑')]
>>> 汇率表 = dict(zip(ls,(6.,7.,8.)))
{('人民币', '美元'): 6.0, ('人民币', '英镑'): 8.0, ('人民币', '欧元'): 7.0}
>>> import pprint
>>> pprint.pprint(汇率表,width=10)
{('人民币', '欧元'): 7.0,
('人民币', '美元'): 6.0,
('人民币', '英镑'): 8.0}
>>> 汇率表[('人民币', '美元')]
6.0黄舟2017-04-18 10:24:18
Sesetengah daripada algoritma di atas sangat rumit untuk ditulis. Mari kita tulis yang mudah:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>
typedef struct node{
char *str; /*拼接后的字符串*/
float value; /*汇率值*/
}node_t;
int main(int argc, char *argv[])
{
/*用户输入的一序列汇率对应关系*/
static char const *buff[] = {"CNY","GBP","0.116",\
"CNY","RUB","8.406",\
"CNY","AUD","0.184",\
"JPY","RUB","0.5072",\
"USD","EUR", "0.9456"};
int npairs = sizeof(buff)/sizeof(buff[0])/3;
node_t * buf = calloc(1,npairs*sizeof(node_t));
if(NULL == buf){
printf("calloc is null !\n");
return(-1);
}
int i = 0;
int j = 0;
int len = 0;
char tmp[16] = {'[field@learn]$./test_hello
please input the two node:
CNY GBP
CNY->GBP 0.116000
[field@learn]$./test_hello
please input the two node:
GBP CNY
CNY->GBP 0.116000
[field@learn]$
'};
for(i=0;i<npairs*3; i+= 3){
memset(tmp,'rrreee',sizeof(tmp));
/*把两个字符串进行拼接*/
snprintf(tmp,16,"%s%s",buff[i],buff[i+1]);
len = strlen(tmp);
buf[j].str = calloc(1,sizeof(char)*(len+1));
if(NULL != buf[j].str){
memmove(buf[j].str,tmp,len);
buf[j].value = atof(buff[i+2]);
j += 1;
}
}
printf("please input the two node:\n");
char input0[8] = {'rrreee'};
char input1[8] = {'rrreee'};
scanf("%s%s",input0,input1);
char data0[16] = {'rrreee'};
char data1[16] = {'rrreee'};
/*考虑正序和反序*/
snprintf(data0,16,"%s%s",input0,input1);
snprintf(data1,16,"%s%s",input1,input0);
for(i=0;i<j;++i){
/*轮训匹配*/
if((0==strcmp(buf[i].str,data0))){
printf("%s->%s %f \n",input0,input1,buf[i].value);
break;
}
if( 0==strcmp(buf[i].str,data1) ){
printf("%s->%s %f \n",input1,input0,buf[i].value);
break;
}
}
if(i==j){
printf("can not find the pair \n");
}
/*
add the free
*/
return 0;
}Keputusan ujian adalah seperti berikut:
rrreeeApa yang digunakan di sini ialah keunikan nama mata wang Kedua-dua mata wang mestilah unik apabila disambungkan bersama.