- masyarakat
- Belajar
- Perpustakaan Alatan
- Masa lapang
Rumah > Soal Jawab > teks badan
问题描述:
n! <= 2^63-1 , 求最大的n.
问题:
如果不用java自带的 Long.MAX_VALUE,这个值,如何表示Long类型的最大值,我的表示方法为啥不对?
我的代码如何修改才能得到正确的值呢?(因为我观察到factorial这个变量从某一刻开始变成0,可能那个时刻就已经求到了最大的n? long类型的factorial范围不够用了?)
有什么优化的算法呢?
/**
* calculate the max value of n that n! < maxValueOf(Long)
* long 8 bytes
* @return max n
*/
private static int findMax() {
long maxLongValue = Long.MAX_VALUE;//(2<<(8*8-1))-1;
System.out.println(maxLongValue);
// n! <= 2^63-1, we recommend algorithm
int n = 5;
while(true){
long factorial =n; //watch out here long
int origin = n;
while(n>1){
factorial *= (n-1);
n--;
}
System.out.println("--------" + factorial);
n = origin;
if((factorial+1) <= maxLongValue){
n++;
System.out.println("n="+ n +" factorial="+factorial);
}else{
n--;
return n;
}
}
}----------下面是结果
/**
* calculate the max value of n that n! < maxValueOf(Long)
* long 8 bytes
* @return max n
*/
private static int findMax() {
long maxLongValue = (1L<<(8*8-1))-1;
System.out.println(maxLongValue);
// n! <= 2^63-1, we recommend algorithm
int n = 5;
long lastFactorial = n;
while(true) {
if (n == 5) {
long firstFactorial = n;//watch out here long
int origin = n;
while (n > 1) {
firstFactorial = firstFactorial * (n - 1);
n--;
}
lastFactorial = firstFactorial;
n = origin + 1;
} else {
//we do worry about currentFactorial*(n-1) cus we never let a variable store it
//in fact we have to worry about currentFactorial*(n-1)
if (lastFactorial <= (maxLongValue/n)) {
if(n==17){
System.out.println("here---for debug only");
}
lastFactorial = lastFactorial * n;
n++;
} else {
return n - 1;
}
}
}
}结果n=20;
----------此外还暴露一个问题,我以为,只要我计算factorialn不存储在某个变凉中就不会又问题,实际上,我太native了,看看下面这个图就知道啦。factorialn不存储,也溢出。。。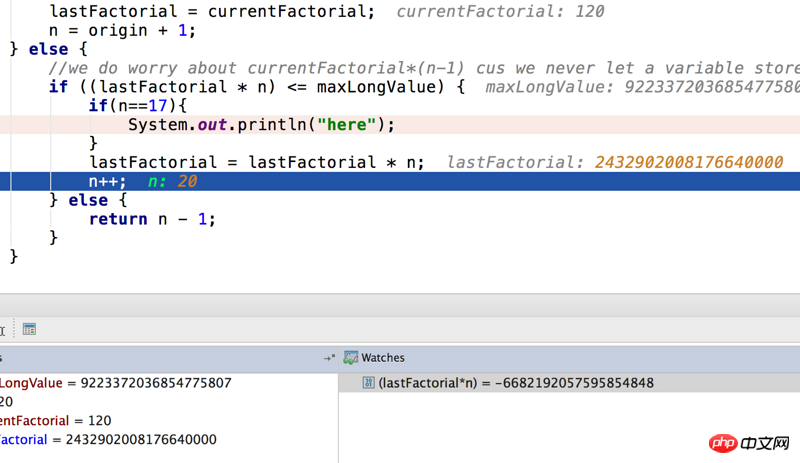
ringa_lee2017-04-17 17:03:50
阶乘结果用BigInteger类型。
---编辑的分割线---
有个很明显的重复计算,因为
n! = n * (n-1)!
所以每一步的结果都可以为下个数的结果所复用,递加乘上次阶乘值即可,不必每个数递减相乘。
判定溢出有个很土的办法,不过貌似可行:
每次n阶乘后判断MAX_VALUE / (n-1) 是否小于 当前阶乘值,是的话相乘必然溢出了。
ringa_lee2017-04-17 17:03:50
(1L << 63)-1 注意必须写1L(long字面量), 不能写1(int字面量)
每个long都一定不大于maxLongValue的, 所以不能用这个来判断溢出. 在已知n!没溢出时可以用(n+1)! / (n+1) == n!来判断.
如果你只需要n (不要阶乘的精确值), 可以用斯特林公式求n!的近似. 但是因为这个搜索范围太小..未必比从1开始逐个算要快.
黄舟2017-04-17 17:03:50
据我所知,不用Long.MAX_VALUE你就只能直接写数值了。
你的结果之所以不对,是因为你以为fatorial是线程递增的,你认为他会慢慢的递增直接到达maxLongValue-1,然而现实是它会在某时(n-1)!< maxLongValue-1,n!>maxLongValue,因溢出,故n!<0,所以继续小于maxLongValue,进入if语句的内容,故的程序会无休止的死循环。改进方法很简单,因为0!=1>0,所以你只要检测factorial何时突变为负数即可。
可能可以优化,然而我不会……
大家讲道理2017-04-17 17:03:50
经过仔细翻书查看:
得出java中,第一次上溢和下溢规律(可能循环上溢或者下溢)(有不妥的地方请给予批评和指正)
上溢: x-2(max+1);
下溢: x+2(max+1);
可以根据溢出规则来,判断溢出。。