Rumah >Peranti teknologi >AI >Transformer mahu menjadi Kansformer? MLP yang telah menghabiskan beberapa dekad menyambut KAN pencabar
Transformer mahu menjadi Kansformer? MLP yang telah menghabiskan beberapa dekad menyambut KAN pencabar
- 王林ke hadapan
- 2024-05-03 13:01:041203semak imbas
MLP (Multilayer Perceptron) telah digunakan selama berpuluh tahun Adakah benar-benar tiada pilihan lain?
Multilayer Perceptron (MLP), juga dikenali sebagai suapan hadapan Rangkaian Neural yang disambungkan sepenuhnya, ialah blok binaan asas model pembelajaran mendalam hari ini.
Kepentingan MLP tidak boleh dilebih-lebihkan kerana ia adalah kaedah lalai untuk menganggarkan fungsi bukan linear dalam pembelajaran mesin.
Walau bagaimanapun, adakah MLP adalah regressor tak linear terbaik yang boleh kita bina? Walaupun MLP digunakan secara meluas, ia mempunyai kelemahan yang ketara. Contohnya, dalam model Transformer, MLP menggunakan hampir semua parameter tidak terbenam dan secara amnya kurang boleh ditafsir berbanding lapisan perhatian tanpa alat analisis pasca pemprosesan.
Jadi, adakah alternatif untuk MLP?
Hari ini, KAN muncul.

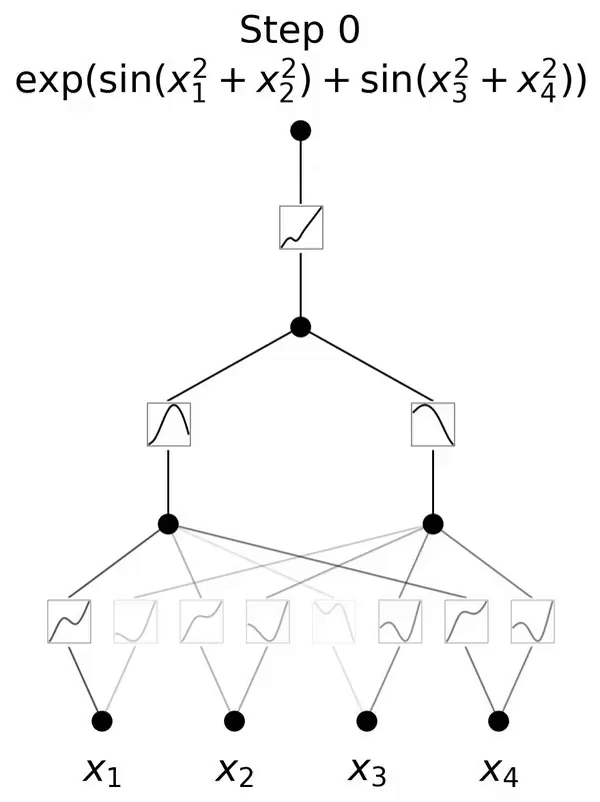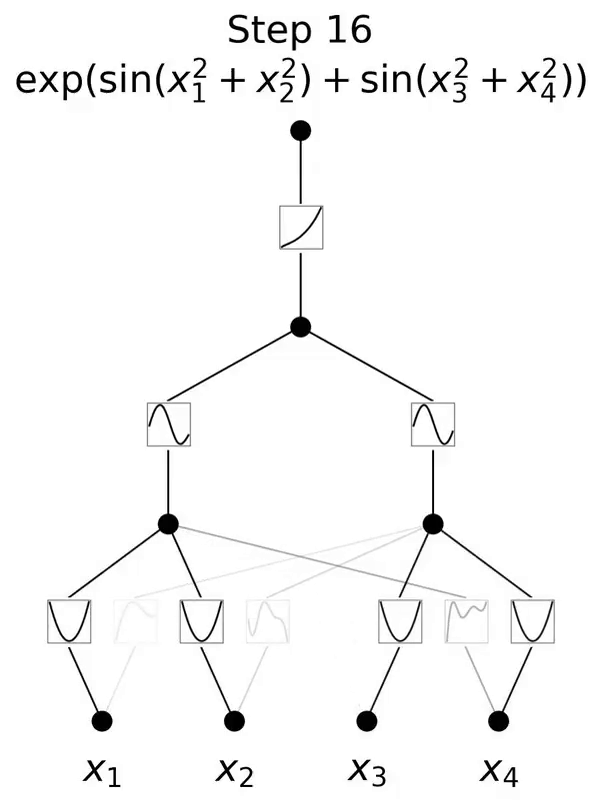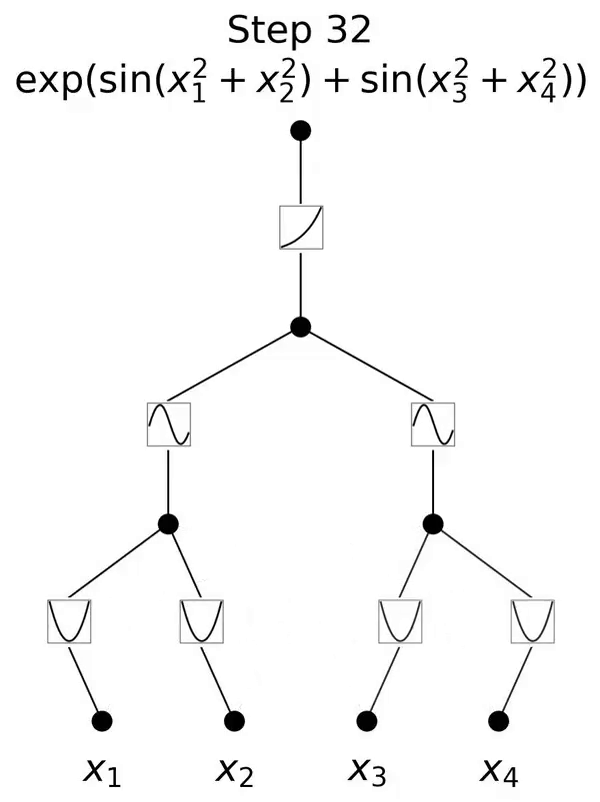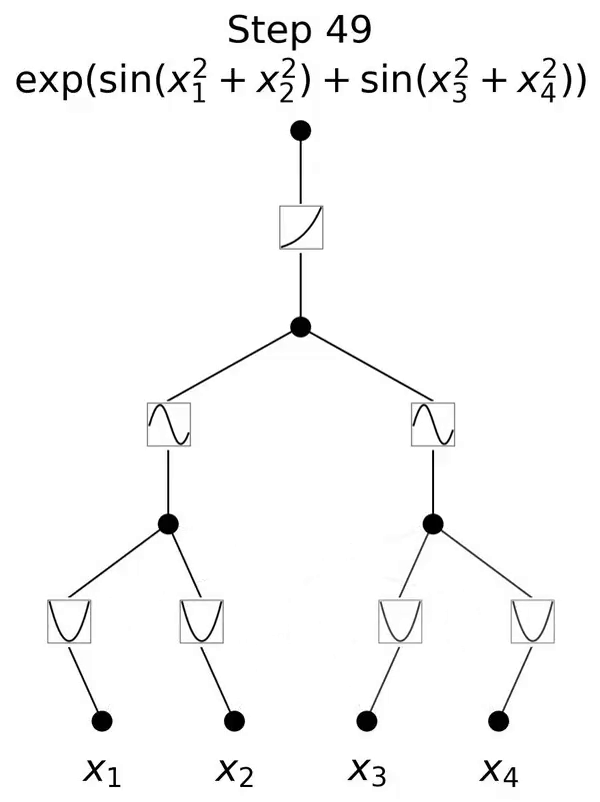

Ini adalah rangkaian yang diilhamkan oleh teorem perwakilan Kolmogorov-Arnold.
Pautan: https://arxiv.org/pdf/2404.19756
Github: https://github.com/KindXiaoming/pykan
Sejurus selepas kajian itu dikeluarkan di platform sosial asing perhatian dan perbincangan yang meluas.
Sesetengah netizen berkata bahawa Kolmogorov menemui rangkaian neural berbilang lapisan seawal tahun 1957, jauh lebih awal daripada kertas kerja Rumerhart, Hinton dan William pada 1986, tetapi dia tidak diendahkan oleh Barat.

Sebilangan netizen juga mengatakan bahawa penerbitan kertas ini bermakna loceng maut pembelajaran mendalam telah kedengaran.

Sesetengah netizen tertanya-tanya sama ada kajian ini akan mengganggu seperti kertas Transformer.

Tetapi sesetengah pengarang berkata bahawa mereka melakukan perkara yang sama berdasarkan teknik Kolmogrov-Gabor yang dipertingkatkan pada 2018-19.
Seterusnya, mari kita lihat tentang apa kertas ini?
Gambaran Keseluruhan Kertas
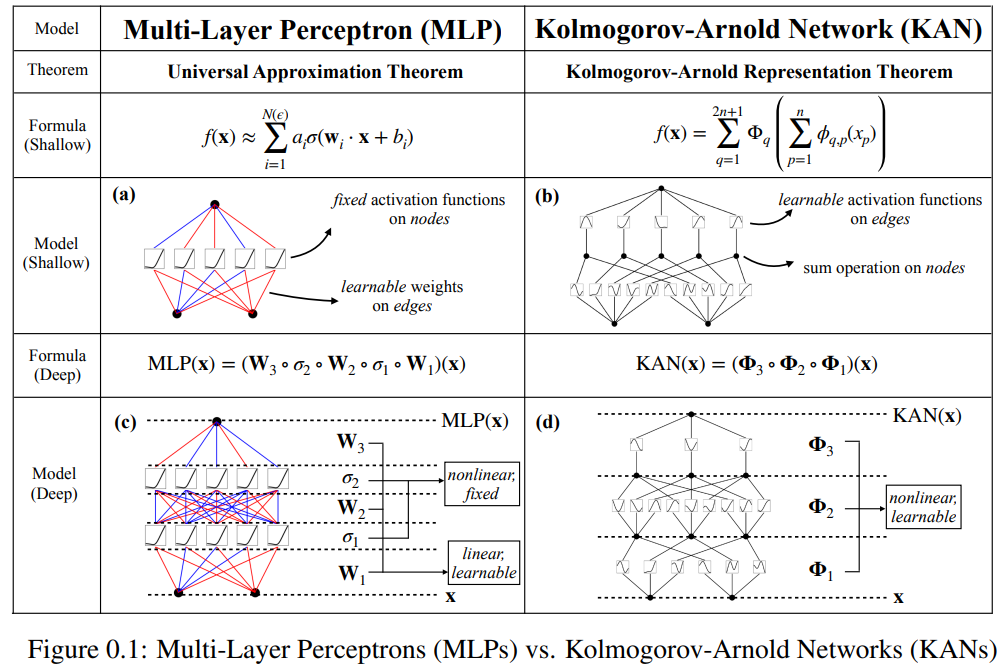
Kertas kerja ini mencadangkan alternatif yang menjanjikan kepada perceptron berbilang lapisan (MLP) yang dipanggil Kolmogorov-Arnold Networks (KAN). Reka bentuk MLP diilhamkan oleh teorem penghampiran universal, manakala reka bentuk KAN diinspirasikan oleh teorem perwakilan Kolmogorov-Arnold. Sama seperti MLP, KAN mempunyai struktur bersambung sepenuhnya. Manakala MLP meletakkan fungsi pengaktifan tetap pada nod (neuron), KAN meletakkan fungsi pengaktifan yang boleh dipelajari pada tepi (berat), seperti yang ditunjukkan dalam Rajah 0.1. Oleh itu, KAN tidak mempunyai matriks berat linear sama sekali: setiap parameter berat digantikan dengan fungsi satu dimensi yang boleh dipelajari yang diparameterkan sebagai spline. Nod KAN hanya menjumlahkan isyarat masuk tanpa menggunakan sebarang transformasi tak linear.
Sesetengah orang mungkin bimbang kos KAN terlalu tinggi kerana parameter berat setiap MLP menjadi fungsi spline KAN. Walau bagaimanapun, KAN membenarkan graf pengiraan yang lebih kecil daripada MLP. Sebagai contoh, penyelidik menunjukkan bahawa penyelesaian PED: KAN dua lapisan dengan lebar 10 adalah 100 kali lebih tepat daripada MLP empat lapisan dengan lebar 100 (MSE ialah 10^-7 dan 10^-5 masing-masing) , dan juga lebih baik dalam kecekapan parameter Dipertingkatkan sebanyak 100 kali (bilangan parameter masing-masing ialah 10^2 dan 10^4).
Kemungkinan menggunakan teorem perwakilan Kolmogorov-Arnold untuk membina rangkaian saraf telah dikaji. Walau bagaimanapun, kebanyakan kerja tersekat pada perwakilan depth-2, width (2n + 1) asal, dan tiada peluang untuk memanfaatkan teknik yang lebih moden (cth., perambatan belakang) untuk melatih rangkaian. Sumbangan artikel ini adalah untuk menyamaratakan perwakilan Kolmogorov-Arnold asal kepada lebar dan kedalaman sewenang-wenangnya, menjadikannya dihidupkan semula dalam bidang pembelajaran mendalam hari ini, sambil menggunakan sejumlah besar eksperimen empirikal untuk menyerlahkan potensi peranannya sebagai model asas "AI + sains" , yang mendapat manfaat daripada ketepatan dan kebolehtafsiran KAN.
Walaupun KAN mempunyai keupayaan penjelasan matematik yang baik, ia sebenarnya hanya gabungan splines dan MLP, mengambil kesempatan daripada kelebihan kedua-duanya dan mengelakkan keburukan. Splines sangat tepat pada fungsi dimensi rendah, mudah dilaraskan secara setempat dan boleh bertukar antara resolusi yang berbeza. Walau bagaimanapun, kerana spline tidak dapat mengeksploitasi struktur gabungan, ia mengalami masalah COD yang teruk. MLP, sebaliknya, kurang terjejas oleh COD kerana keupayaan pembelajaran ciri mereka, tetapi tidak setepat spline dalam ruang dimensi rendah kerana ia tidak dapat mengoptimumkan fungsi univariate.
Untuk mempelajari fungsi dengan tepat, model bukan sahaja harus mempelajari struktur gabungan (darjah kebebasan luar), tetapi juga menghampiri fungsi univariat (darjah kebebasan dalaman) dengan baik. KAN adalah model sedemikian kerana ia menyerupai MLP secara luaran dan spline secara dalaman. Hasilnya, KAN bukan sahaja boleh mempelajari ciri (berkat persamaan luarannya dengan MLP) tetapi juga mengoptimumkan ciri yang dipelajari ini kepada ketepatan yang sangat tinggi (berkat persamaan dalaman mereka dengan spline).
Contohnya, untuk fungsi berdimensi tinggi:
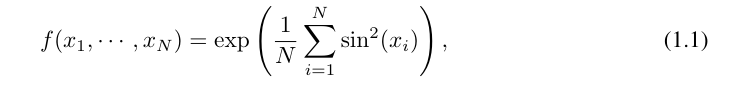
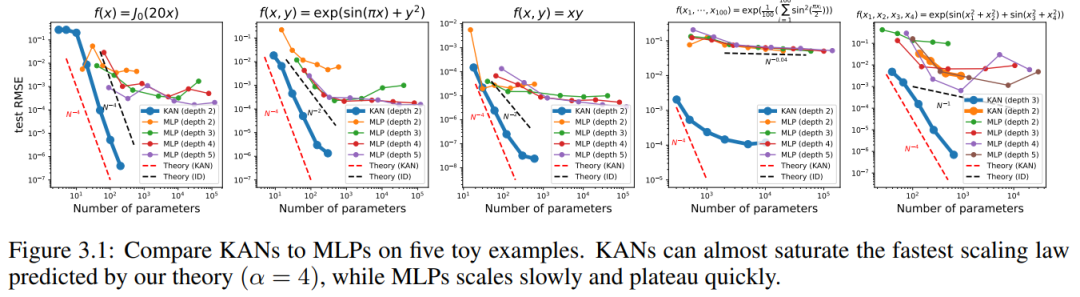
Apabila N besar, spline akan gagal kerana COD walaupun mungkin untuk MLP mempelajari struktur aditif umum, ia menggunakan, sebagai contoh, a Fungsi pengaktifan ReLU untuk menganggarkan fungsi eksponen dan sinus adalah sangat tidak cekap. Sebaliknya, KAN dapat mempelajari struktur gabungan dan fungsi univariat dengan sangat baik, sekali gus mengatasi prestasi MLP dengan margin yang besar (lihat Rajah 3.1).
Dalam kertas kerja ini, penyelidik menunjukkan sejumlah besar nilai eksperimen, yang mencerminkan peningkatan ketara KAN dalam MLP dari segi ketepatan dan kebolehtafsiran. Struktur kertas ditunjukkan dalam Rajah 2.1 di bawah. Kod ini boleh didapati di https://github.com/KindXiaoming/pykan dan juga boleh dipasang melalui pip install pykan.
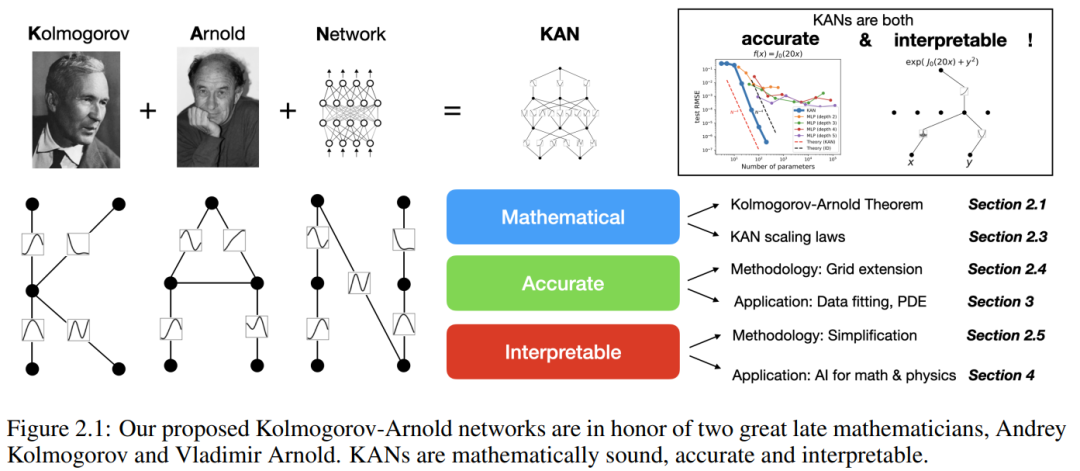
Kolmogorov-Arnold Network (KAN)
Kolmogorov-Arnold Representation Theorem
Vladimir f Arnold dan Andrey Kolmogorov yang boleh ditulis sebagai pembolehubah boleh dibuktikan pada domain boleh berbilang f, Andrey Kolmogorov yang boleh dibuktikan pada domain boleh berbilang f jika berterusan. gabungan terhingga bagi fungsi berterusan pembolehubah tunggal dan operasi penambahan binari. Lebih khusus lagi, untuk fungsi lancar f : [0, 1]^n → R, ia boleh dinyatakan sebagai:
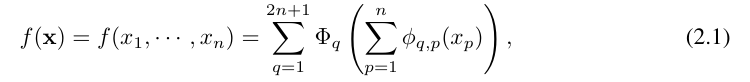 di mana
di mana 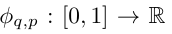 dan
dan 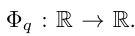
Dalam satu erti kata, mereka mempamerkan satu-satunya multivariate sebenar Fungsi ini adalah aditif kerana semua fungsi lain boleh diwakili oleh fungsi pembolehubah tunggal dan penjumlahan. Seseorang mungkin berfikir bahawa ini adalah berita baik untuk pembelajaran mesin: mempelajari fungsi dimensi tinggi bermuara kepada mempelajari fungsi satu dimensi dalam kuantiti polinomial. Walau bagaimanapun, fungsi satu dimensi ini mungkin tidak licin atau fraktal dan oleh itu mungkin tidak dipelajari dalam amalan. Oleh itu, teorem perwakilan Kolmogorov-Arnold pada dasarnya adalah hukuman mati dalam pembelajaran mesin, dianggap betul secara teori tetapi praktikalnya tidak berguna.
Walau bagaimanapun, penyelidik lebih optimistik tentang kepraktisan teorem Kolmogorov-Arnold dalam pembelajaran mesin. Pertama, tidak perlu berpegang pada persamaan asal, yang hanya mempunyai dua lapisan tidak linear dan sebilangan kecil istilah (2n + 1) dalam lapisan tersembunyi: penyelidik akan menyamaratakan rangkaian kepada lebar dan kedalaman sewenang-wenangnya. Kedua, kebanyakan fungsi dalam sains dan kehidupan harian biasanya lancar dan mempunyai struktur gabungan yang jarang, yang boleh memudahkan perwakilan Kolmogorov-Arnold yang lancar.
KAN Seni Bina
Andaikan terdapat tugas pembelajaran yang diselia yang terdiri daripada pasangan input dan output {x_i, y_i}, dan penyelidik berharap untuk mencari fungsi f sedemikian rupa sehingga y_i ≈ f (x_i) untuk semua titik data. Persamaan (2.1) bermaksud bahawa jika fungsi pembolehubah tunggal yang sesuai 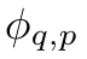 dan
dan 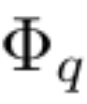 boleh ditemui, maka tugas itu tercapai. Ini memberi inspirasi kepada penyelidik untuk mereka bentuk rangkaian saraf yang secara eksplisit meparameterkan persamaan (2.1). Memandangkan semua fungsi yang perlu dipelajari adalah fungsi univariate, pengkaji membuat parameter setiap fungsi satu dimensi sebagai lengkung B-spline dengan pekali boleh dipelajari bagi fungsi asas B-spline tempatan (lihat sebelah kanan Rajah 2.2). Kami kini mempunyai prototaip KAN, yang graf pengiraannya ditentukan sepenuhnya oleh persamaan (2.1) dan digambarkan dalam Rajah 0.1(b) (dimensi input n = 2), yang kelihatan seperti rangkaian neural dua lapisan dengan fungsi pengaktifan diletakkan pada tepi dan bukannya nod (penjumlahan mudah dilakukan pada nod), dan lebar lapisan tengah ialah 2n + 1.
boleh ditemui, maka tugas itu tercapai. Ini memberi inspirasi kepada penyelidik untuk mereka bentuk rangkaian saraf yang secara eksplisit meparameterkan persamaan (2.1). Memandangkan semua fungsi yang perlu dipelajari adalah fungsi univariate, pengkaji membuat parameter setiap fungsi satu dimensi sebagai lengkung B-spline dengan pekali boleh dipelajari bagi fungsi asas B-spline tempatan (lihat sebelah kanan Rajah 2.2). Kami kini mempunyai prototaip KAN, yang graf pengiraannya ditentukan sepenuhnya oleh persamaan (2.1) dan digambarkan dalam Rajah 0.1(b) (dimensi input n = 2), yang kelihatan seperti rangkaian neural dua lapisan dengan fungsi pengaktifan diletakkan pada tepi dan bukannya nod (penjumlahan mudah dilakukan pada nod), dan lebar lapisan tengah ialah 2n + 1.
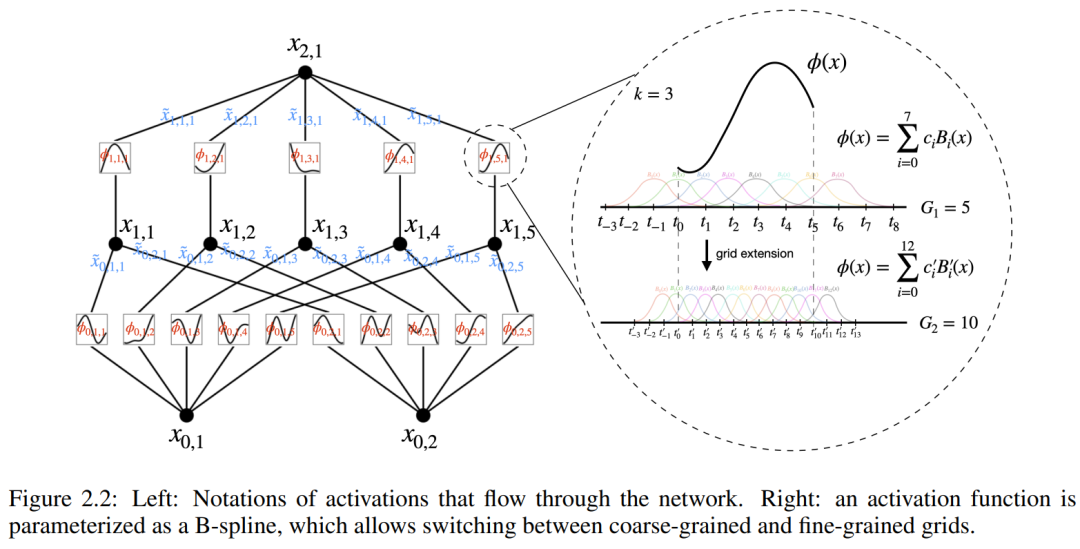
Seperti yang dinyatakan sebelum ini, dalam praktiknya rangkaian sedemikian dianggap terlalu mudah untuk menganggarkan sebarang fungsi dengan spline melicinkan dengan ketepatan sewenang-wenangnya. Oleh itu, penyelidik membuat generalisasi KAN kepada rangkaian yang lebih luas dan mendalam. Memandangkan perwakilan Kolmogorov-Arnold sepadan dengan KAN dua lapisan, tidak jelas bagaimana untuk menjadikan KAN lebih dalam.
Titik terobosan ialah para penyelidik melihat analogi antara MLP dan KAN. Dalam MLP, sebaik sahaja lapisan (terdiri daripada transformasi linear dan bukan linear) ditakrifkan, lebih banyak lapisan boleh disusun untuk menjadikan rangkaian lebih mendalam. Untuk membina KAN yang mendalam, anda harus terlebih dahulu menjawab: "Apakah lapisan KAN?" Penyelidik mendapati bahawa lapisan KAN dengan input n_in-dimensi dan output n_out-dimensi boleh ditakrifkan sebagai matriks fungsi satu dimensi.
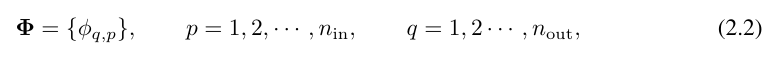
di mana fungsi  mempunyai parameter yang boleh dilatih seperti yang diterangkan di bawah. Dalam teorem Kolmogorov-Arnold, fungsi dalam membentuk lapisan KAN dengan n_in = n dan n_out = 2n+1, dan fungsi luar membentuk lapisan KAN dengan n_in = 2n + 1 dan n_out = 1. Oleh itu, perwakilan Kolmogorov-Arnold dalam persamaan (2.1) hanyalah gabungan dua lapisan KAN. Sekarang, mempunyai perwakilan Kolmogorov-Arnold yang lebih mendalam bermakna: hanya susun lebih banyak lapisan KAN!
mempunyai parameter yang boleh dilatih seperti yang diterangkan di bawah. Dalam teorem Kolmogorov-Arnold, fungsi dalam membentuk lapisan KAN dengan n_in = n dan n_out = 2n+1, dan fungsi luar membentuk lapisan KAN dengan n_in = 2n + 1 dan n_out = 1. Oleh itu, perwakilan Kolmogorov-Arnold dalam persamaan (2.1) hanyalah gabungan dua lapisan KAN. Sekarang, mempunyai perwakilan Kolmogorov-Arnold yang lebih mendalam bermakna: hanya susun lebih banyak lapisan KAN!
Pemahaman lanjut memerlukan pengenalan beberapa simbol Anda boleh merujuk kepada Rajah 2.2 (kiri) untuk contoh khusus dan pemahaman intuitif. Bentuk KAN diwakili oleh tatasusunan integer:

di mana n_i ialah bilangan nod dalam lapisan ke-i graf pengiraan. Di sini, (l, i) mewakili neuron ke-i bagi lapisan ke-l, dan x_l,i mewakili nilai pengaktifan neuron (l, i). Di antara lapisan l-th dan l + 1-th layer, terdapat n_l*n_l+1 fungsi pengaktifan: fungsi pengaktifan menyambung (l, j) dan (l + 1, i) dinyatakan sebagai

fungsi ϕ_l, Nilai pra-pengaktifan i,j hanya dinyatakan sebagai x_l,i; nilai pasca pengaktifan ϕ_l,i,j ialah 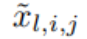 ≡ ϕ_l,i,j (x_l,i). Nilai pengaktifan neuron ke (l + 1, j) ialah jumlah semua nilai pengaktifan masuk:
≡ ϕ_l,i,j (x_l,i). Nilai pengaktifan neuron ke (l + 1, j) ialah jumlah semua nilai pengaktifan masuk:
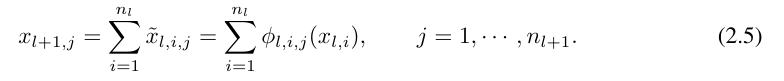
dinyatakan dalam bentuk matriks seperti berikut:

di mana, Φ_l ialah lapisan KAN yang sepadan dengan Matriks fungsi lapisan lth. Rangkaian KAN am ialah gabungan lapisan L: diberi vektor input x_0 ∈ R^n0, output KAN ialah
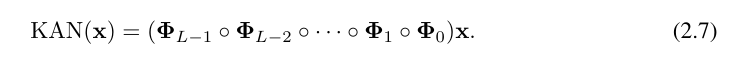
Persamaan di atas juga boleh ditulis dalam situasi yang serupa dengan persamaan (2.1), dengan andaian bahawa dimensi output n_L = 1, dan takrifkan f (x) ≡ KAN (x):
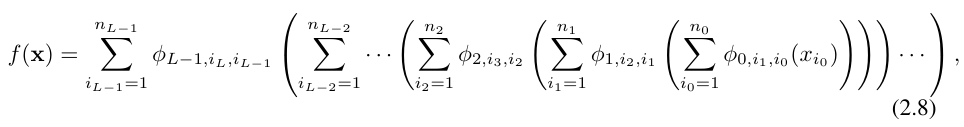
Menulis begini agak memenatkan. Sebaliknya, abstraksi penyelidik lapisan KAN dan visualisasinya adalah lebih ringkas dan intuitif. Perwakilan Kolmogorov-Arnold asal (2.1) sepadan dengan KAN 2 lapisan bentuk [n, 2n + 1, 1]. Ambil perhatian bahawa semua operasi boleh dibezakan, jadi KAN boleh dilatih dengan perambatan belakang. Sebagai perbandingan, MLP boleh ditulis sebagai jalinan penjelmaan affine W dan bukan linear σ:
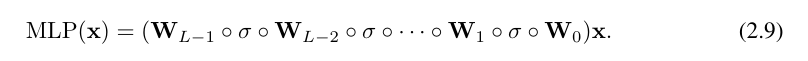
Jelas sekali, MLP memproses transformasi linear dan bukan linear masing-masing sebagai W dan σ, manakala KAN memprosesnya bersama-sama sebagai Φ. Dalam Rajah 0.1 (c) dan (d), penyelidik menunjukkan MLP tiga lapisan dan KAN tiga lapisan untuk menggambarkan perbezaan antara mereka.
Ketepatan KAN
Dalam kertas kerja, penulis juga menunjukkan bahawa KAN lebih berkesan daripada MLP dalam mewakili fungsi dalam pelbagai tugas (regresi dan penyelesaian persamaan pembezaan separa). Dan mereka juga menunjukkan bahawa KAN secara semula jadi boleh berfungsi dalam pembelajaran berterusan tanpa pelupaan bencana.
toy Dataset
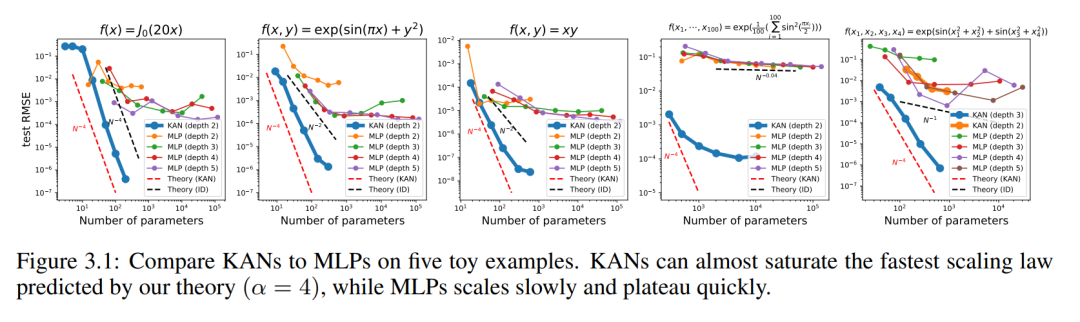
Kami memplot ujian RMSE KAN dan MLP sebagai fungsi bilangan parameter dalam Rajah 3.1, menunjukkan bahawa KAN mempunyai lengkung penskalaan yang lebih baik daripada MLP, terutamanya dalam contoh berdimensi tinggi. Sebagai perbandingan, penulis merancang garis yang diramalkan mengikut teori KAN mereka, sebagai garis putus-putus merah (α = k + 1 = 4), dan garis yang diramalkan mengikut Sharma & Kaplan [17], sebagai garis putus-putus hitam (α = (k + 1 )/d = 4/d). KAN hampir boleh mengisi garis merah yang lebih curam, manakala MLP juga bergelut untuk menumpu pada kadar garis hitam yang lebih perlahan dan cepat mencapai dataran tinggi. Penulis juga ambil perhatian bahawa untuk contoh terakhir, KAN 2 lapisan berprestasi lebih teruk daripada KAN 3 lapisan (bentuk [4, 2, 2, 1]). Ini menyerlahkan bahawa KAN yang lebih dalam adalah lebih ekspresif, dan perkara yang sama berlaku untuk MLP: MLP yang lebih dalam adalah lebih ekspresif daripada MLP yang lebih cetek.
Fungsi khas
Kami menunjukkan dua perkara berikut dalam bahagian ini:
(1) Adalah mungkin untuk mencari (kira-kira) perwakilan KA padat bagi fungsi khas, yang didedahkan dari perspektif Kolmogorov- Perwakilan Arnold Sifat matematik baharu bagi fungsi khas.
(2) KAN lebih cekap dan tepat daripada MLP dalam mewakili fungsi khas.
Untuk setiap set data dan setiap keluarga model (KAN atau MLP), penulis memplot sempadan Pareto pada bilangan parameter dan satah RMSE, seperti ditunjukkan dalam Rajah 3.2.
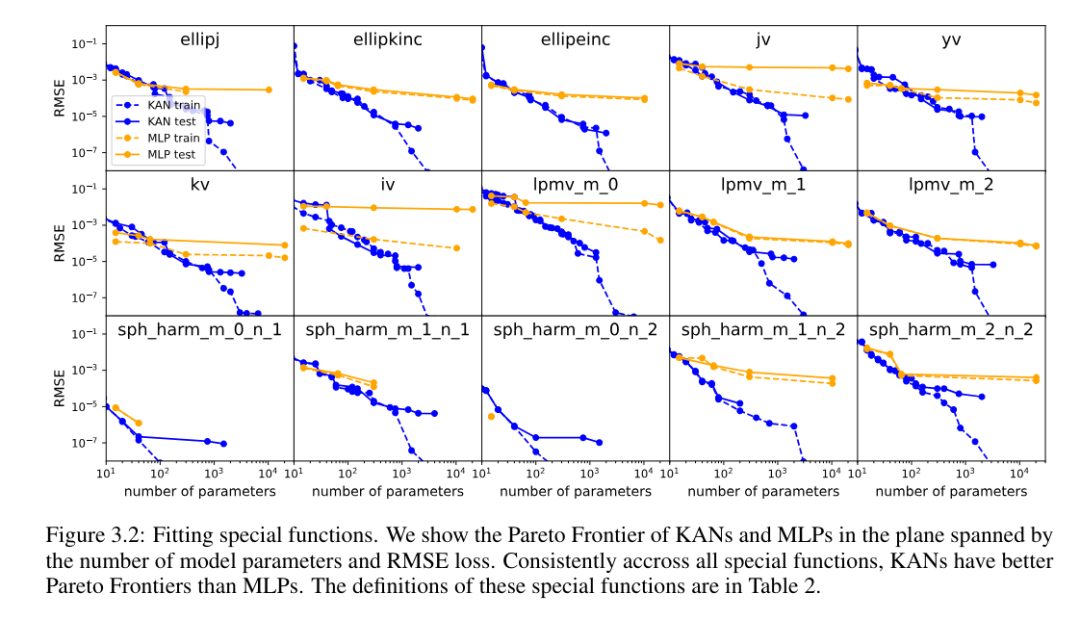
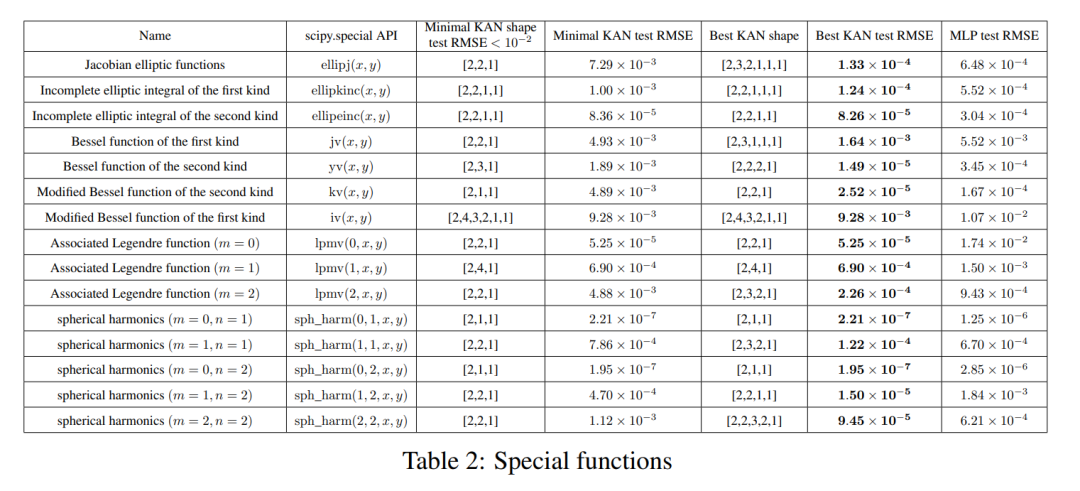
KAN secara konsisten menunjukkan prestasi yang lebih baik daripada MLP, iaitu, dengan bilangan parameter yang sama, KAN mampu mencapai kerugian latihan/ujian yang lebih rendah daripada MLP. Tambahan pula, pengarang melaporkan dalam Jadual 2 bentuk (mengejutkan padat) KAN untuk fungsi khas yang mereka temui secara automatik. Di satu pihak, adalah menarik untuk menerangkan secara matematik maksud perwakilan padat ini. Sebaliknya, perwakilan padat ini bermakna bahawa adalah mungkin untuk menguraikan jadual carian dimensi tinggi kepada beberapa jadual carian satu dimensi, yang berpotensi dapat menjimatkan banyak memori dengan mengorbankan melakukan beberapa operasi penambahan pada masa inferens (hampir boleh diabaikan).
Feynman Dataset
Seting di bahagian sebelum ini ialah kita tahu dengan jelas bentuk KAN yang "sebenar". Persediaan dalam bahagian sebelumnya ialah kita jelas tidak tahu bentuk KAN "sebenar". Bahagian ini mengkaji tetapan perantaraan: memandangkan struktur set data, kami mungkin membina KAN dengan tangan, tetapi kami tidak pasti sama ada ia adalah optimum.
Untuk setiap kombinasi hyperparameter, penulis mencuba 3 biji secara rawak. Bagi setiap set data (persamaan) dan setiap kaedah, mereka melaporkan dalam Jadual 3 keputusan model terbaik (bentuk KAN minimum atau kehilangan ujian terendah) pada benih dan kedalaman rawak.
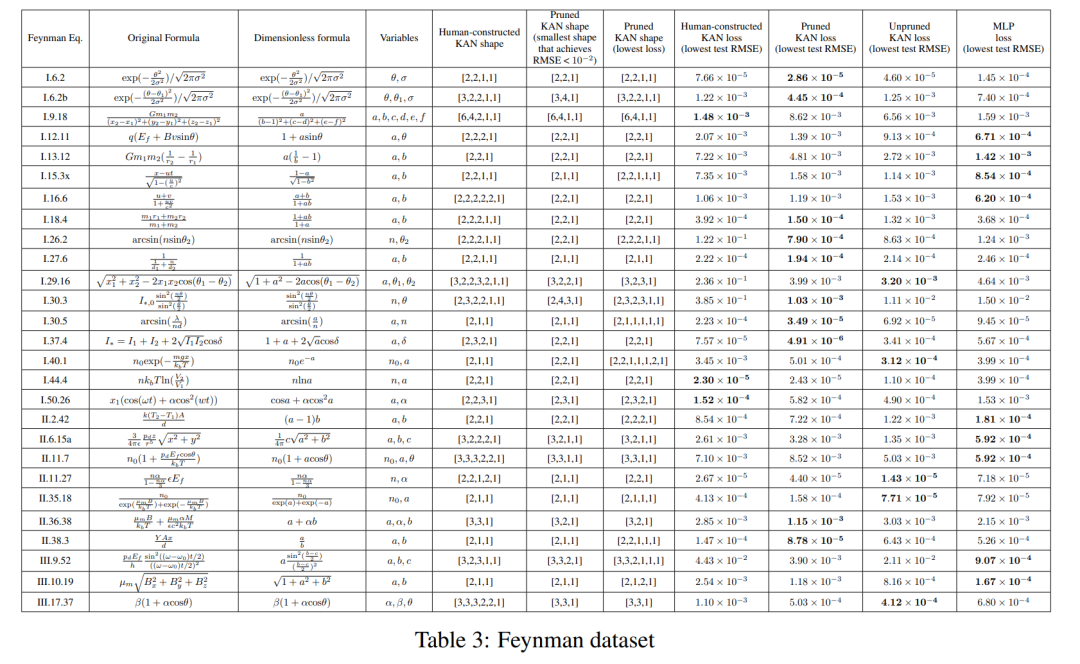
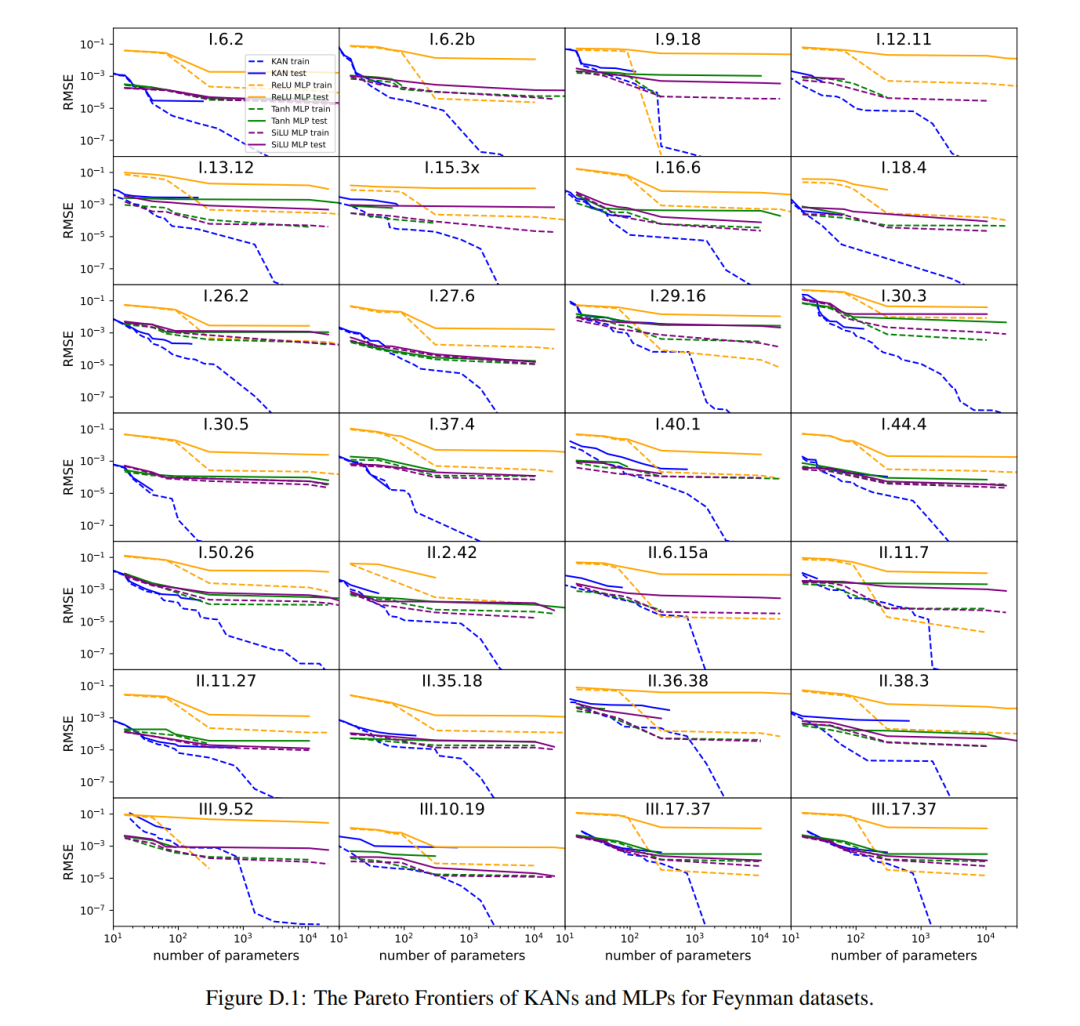
Mereka mendapati bahawa MLP dan KAN berprestasi sama baik secara purata. Bagi setiap set data dan setiap keluarga model (KAN atau MLP), penulis memplot sempadan Pareto pada satah yang dibentuk oleh bilangan parameter dan kehilangan RMSE, seperti ditunjukkan dalam Rajah D.1. Mereka membuat spekulasi bahawa set data Feynman adalah terlalu mudah untuk membenarkan penambahbaikan lanjut oleh KAN, dalam erti kata bahawa kebergantungan berubah-ubah selalunya lancar atau monoton, berbeza dengan kerumitan fungsi khas, yang sering menunjukkan tingkah laku berayun.
Selesaikan persamaan pembezaan separa
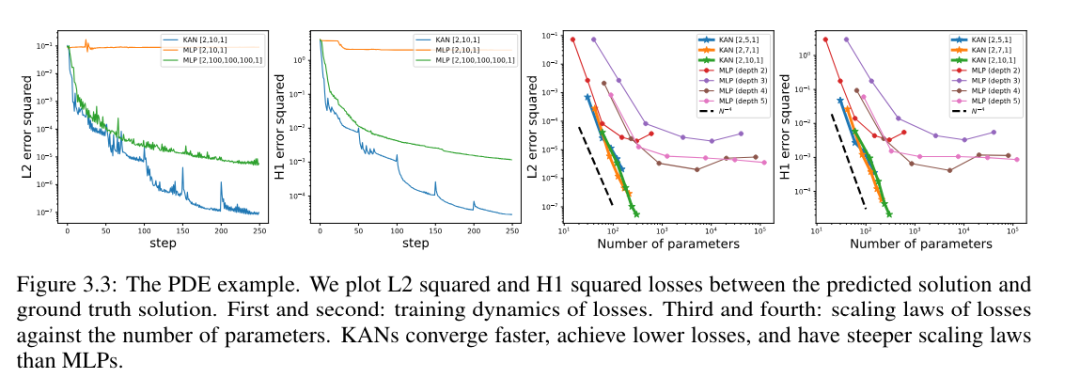
Pengarang membandingkan seni bina KAN dan MLP menggunakan hiperparameter yang sama. Mereka mengukur ralat dalam norma L^2 dan norma tenaga (H^1), dan memerhatikan bahawa KAN mencapai undang-undang penskalaan yang lebih baik dan ralat yang lebih kecil semasa menggunakan rangkaian yang lebih kecil dan parameter yang lebih sedikit, Lihat Rajah 3.3. Oleh itu, mereka membuat spekulasi bahawa KAN mungkin berpotensi untuk berfungsi sebagai perwakilan rangkaian saraf yang baik untuk pengurangan model persamaan pembezaan separa (PDE).
Pembelajaran Berterusan
Pengarang menunjukkan bahawa KAN mempunyai keplastikan tempatan dan boleh mengelakkan pelupaan bencana dengan mengeksploitasi lokaliti spline. Ideanya mudah: memandangkan asas spline adalah setempat, sampel hanya akan mempengaruhi beberapa pekali spline berdekatan, sambil membiarkan pekali jauh tidak berubah (inilah yang kita mahu, kerana kawasan jauh mungkin sudah menyimpan pekali yang kita inginkan maklumat yang disimpan) . Sebaliknya, memandangkan MLP biasanya menggunakan fungsi pengaktifan global seperti ReLU/Tanh/SiLU, dsb., sebarang perubahan setempat mungkin merebak secara tidak terkawal ke kawasan yang jauh, memusnahkan maklumat yang disimpan di sana.
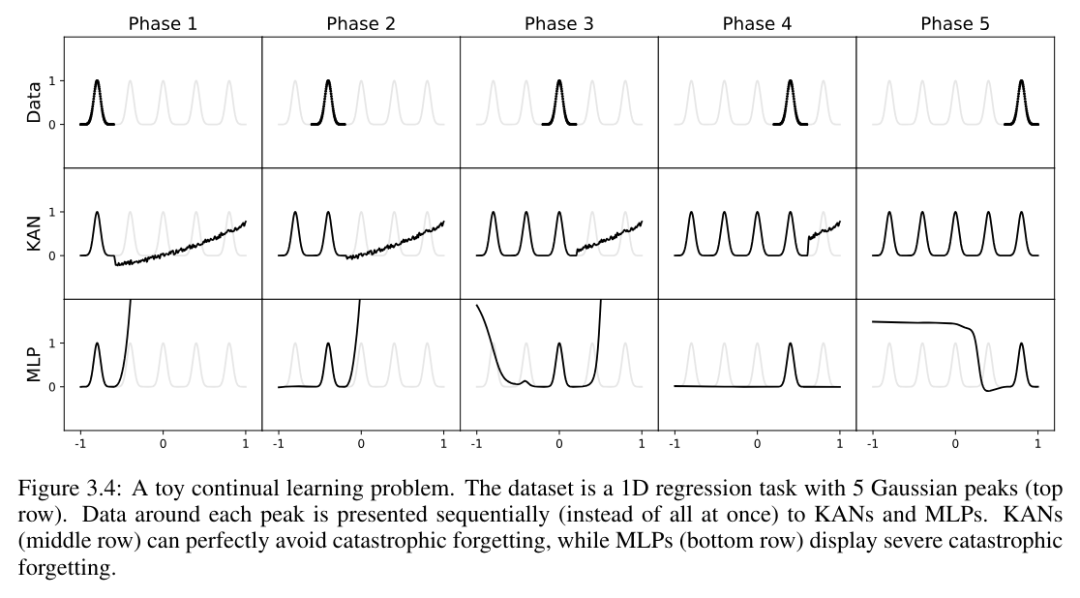
Pengarang menggunakan contoh mudah untuk mengesahkan gerak hati ini. Tugas regresi satu dimensi terdiri daripada 5 puncak Gaussian. Data di sekeliling setiap puncak dibentangkan secara berurutan (bukannya sekali gus), seperti yang ditunjukkan dalam baris atas Rajah 3.4, dibentangkan secara berasingan kepada KAN dan MLP. Keputusan ramalan KAN dan MLP selepas setiap peringkat latihan ditunjukkan di baris tengah dan bawah, masing-masing. Seperti yang dijangkakan, KAN hanya membina semula wilayah yang data wujud pada peringkat semasa, menjadikan wilayah sebelumnya tidak berubah. Sebaliknya, MLP membina semula seluruh rantau selepas melihat sampel data baharu, yang membawa kepada pelupaan bencana.
KAN boleh ditafsirkan
Dalam Bab 4 artikel, penulis menunjukkan bahawa KAN boleh ditafsir dan interaktif terima kasih kepada teknik yang dibangunkan dalam Bahagian 2.5. Mereka ingin menguji aplikasi KAN bukan sahaja pada tugas sintesis (Sekte. 4.1 dan 4.2), tetapi juga dalam penyelidikan saintifik kehidupan sebenar. Mereka menunjukkan bahawa KAN dapat (semula) menemui hubungan kompleks dalam teori simpang (Bahagian 4.3) dan sempadan peralihan fasa dalam fizik jirim pekat (Bahagian 4.4). Disebabkan ketepatan dan kebolehtafsirannya, KAN berpotensi untuk menjadi model asas untuk AI + Sains.
Perbincangan
Dalam kertas kerja, penulis membincangkan batasan dan hala tuju pembangunan masa depan KAN dari perspektif asas matematik, algoritma dan aplikasi.
Aspek matematik: Walaupun penulis telah melakukan analisis matematik awal KAN (Teorem 2.1), pemahaman matematik mereka masih sangat terhad. Teorem perwakilan Kolmogorov-Arnold telah dikaji secara matematik dengan teliti, tetapi ia sepadan dengan KAN bentuk [n, 2n + 1, 1], yang merupakan subkelas KAN yang sangat terhad. Adakah kejayaan empirikal pada KAN yang lebih mendalam membayangkan sesuatu yang asas secara matematik? Teorem umum Kolmogorov-Arnold yang menarik boleh mentakrifkan perwakilan Kolmogorov-Arnold yang "lebih mendalam" melebihi gabungan dua lapisan, dan berpotensi mengaitkan kelancaran fungsi pengaktifan dengan kedalaman. Katakan terdapat fungsi yang tidak boleh diwakili dengan lancar dalam perwakilan asal (kedalaman 2) Kolmogorov-Arnold, tetapi mungkin diwakili dengan lancar pada kedalaman 3 atau lebih dalam. Bolehkah kita menggunakan konsep "Kolmogorov-Arnold depth" ini untuk mencirikan kelas fungsi?
Dari segi algoritma, mereka membincangkan perkara berikut:
Ketepatan. Terdapat berbilang pilihan dalam reka bentuk dan latihan seni bina yang belum disiasat sepenuhnya, jadi mungkin terdapat alternatif untuk meningkatkan lagi ketepatan. Sebagai contoh, fungsi pengaktifan spline mungkin digantikan dengan fungsi asas jejari atau fungsi inti tempatan yang lain. Strategi grid penyesuaian boleh digunakan.
Kecekapan. Salah satu sebab utama mengapa KAN lambat adalah kerana fungsi pengaktifan yang berbeza tidak dapat memanfaatkan pengiraan kelompok (sebilangan besar data yang melalui fungsi yang sama). Malah, kita boleh interpolasi antara MLP (semua fungsi pengaktifan adalah sama) dan KAN (semua fungsi pengaktifan adalah berbeza) dengan mengumpulkan fungsi pengaktifan ke dalam kumpulan ("berbilang"), di mana ahli kumpulan berkongsi fungsi pengaktifan yang sama.
Campuran KAN dan MLP. Berbanding dengan MLP, KAN mempunyai dua perbezaan utama:
(i) Fungsi pengaktifan terletak di tepi dan bukannya nod
(ii) Fungsi pengaktifan boleh dipelajari dan bukannya tetap.
Perubahan manakah yang lebih menjelaskan kelebihan KAN? Penulis membentangkan hasil awal mereka dalam Lampiran B, di mana mereka mengkaji model dengan (ii), iaitu fungsi pengaktifan boleh dipelajari (seperti KAN), tetapi tanpa (i), iaitu fungsi pengaktifan terletak di nod (Seperti MLP ). Selain itu, seseorang boleh membina model lain yang fungsi pengaktifannya tetap (seperti MLP) tetapi terletak di tepi (seperti KAN).
Kebolehsuaian. Disebabkan lokaliti yang wujud bagi fungsi asas spline, kami boleh memperkenalkan penyesuaian dalam reka bentuk dan latihan KAN untuk meningkatkan ketepatan dan kecekapan: lihat [93, 94] untuk idea latihan pelbagai peringkat seperti kaedah multigrid atau fungsi asas bergantung kepada Domain seperti kaedah berbilang skala dalam [95].
Aplikasi: Penulis telah membentangkan beberapa bukti awal bahawa KAN lebih berkesan daripada MLP dalam tugas berkaitan sains, seperti menyesuaikan persamaan fizik dan menyelesaikan PDE. Mereka menjangkakan bahawa KAN juga mungkin menjanjikan dalam menyelesaikan persamaan Navier-Stokes, teori fungsi ketumpatan, atau sebarang tugas lain yang boleh dirumuskan sebagai penyelesaian regresi atau PDE. Mereka juga berharap untuk menggunakan KAN pada tugas yang berkaitan dengan pembelajaran mesin, yang memerlukan penyepaduan KAN ke dalam seni bina semasa, seperti transformer - seseorang boleh mencadangkan "kansformers" untuk menggantikan MLP dengan KAN dalam transformer.
KAN sebagai Model Bahasa untuk AI + Sains: Model bahasa yang besar adalah transformatif kerana ia berguna kepada sesiapa sahaja yang boleh menggunakan bahasa semula jadi. Bahasa sains adalah fungsi. KAN terdiri daripada fungsi yang boleh ditafsir, jadi apabila pengguna manusia merenung KAN, ia seperti berkomunikasi dengannya menggunakan bahasa berfungsi. Perenggan ini bertujuan untuk menekankan paradigma kolaborasi AI-saintis dan bukannya alat khusus KAN. Sama seperti orang menggunakan bahasa yang berbeza untuk berkomunikasi, penulis meramalkan bahawa pada masa akan datang KAN hanya akan menjadi salah satu bahasa sains AI +, walaupun KAN akan menjadi salah satu bahasa pertama yang membolehkan AI dan manusia untuk berkomunikasi. Walau bagaimanapun, terima kasih kepada pembolehan KAN, paradigma kolaborasi AI-saintis tidak pernah menjadi lebih mudah dan lebih mudah, membuatkan kita berfikir semula bagaimana kita mahu mendekati sains AI +: Adakah kita mahu saintis AI, atau adakah kita mahu AI yang membantu saintis? Kesukaran yang wujud untuk saintis dalam AI (automatik sepenuhnya) ialah kesukaran untuk mengukur keutamaan manusia, yang akan mengkodifikasikan pilihan manusia ke dalam matlamat AI. Malah, saintis dalam bidang yang berbeza mungkin mempunyai perasaan yang berbeza tentang fungsi mana yang mudah atau boleh ditafsir. Oleh itu, adalah lebih baik untuk saintis mempunyai AI yang boleh bercakap dalam bahasa sains (fungsi) dan boleh berinteraksi dengan mudah dengan bias induktif saintis individu agar sesuai dengan domain saintifik tertentu.
Soalan utama: KAN atau MLP?
Pada masa ini, kesesakan terbesar KAN ialah kelajuan latihannya yang perlahan. Dengan bilangan parameter yang sama, masa latihan KAN biasanya 10 kali ganda daripada MLP. Penulis menyatakan bahawa, secara jujur, mereka tidak berusaha untuk mengoptimumkan kecekapan KAN, jadi mereka percaya bahawa kelajuan latihan KAN yang perlahan adalah lebih kepada isu kejuruteraan yang boleh diperbaiki pada masa hadapan dan bukannya batasan asas. Jika seseorang ingin melatih model dengan cepat, dia harus menggunakan MLP. Walau bagaimanapun, dalam kes lain, KAN sepatutnya sebaik atau lebih baik daripada MLP, menjadikannya berbaloi untuk dicuba. Pohon keputusan dalam Rajah 6.1 boleh membantu menentukan masa untuk menggunakan KAN. Ringkasnya, jika anda mementingkan kebolehtafsiran dan/atau ketepatan, dan latihan yang perlahan bukanlah isu utama, penulis mengesyorkan mencuba KAN.
Untuk butiran lanjut, sila baca kertas asal.
Atas ialah kandungan terperinci Transformer mahu menjadi Kansformer? MLP yang telah menghabiskan beberapa dekad menyambut KAN pencabar. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- git常用命令大全【建议收藏】
- Bagaimana untuk membatalkan komit git
- Artikel ciri|Permintaan untuk kuasa pengkomputeran meletup di bawah ledakan model besar AI: Lingang mahu membina industri berpuluh-puluh bilion, dan SenseTime akan menjadi 'tuan rantai'
- Baidu melancarkan model perubatan 'peringkat industri' pertama China 'Model Perubatan Rohani': Baidu melancarkan model perubatan 'peringkat industri' pertama China 'Model Perubatan Rohani'
- Bagaimanakah robot kolaboratif boleh memperkasakan pembuatan dan peningkatan pintar industri kimia harian? Dengar apa yang pakar katakan

