Caltech Cina menggunakan AI untuk menumbangkan bukti matematik! Mempercepatkan 5 kali terkejut Tao Zhexuan, 80% langkah matematik adalah automatik sepenuhnya

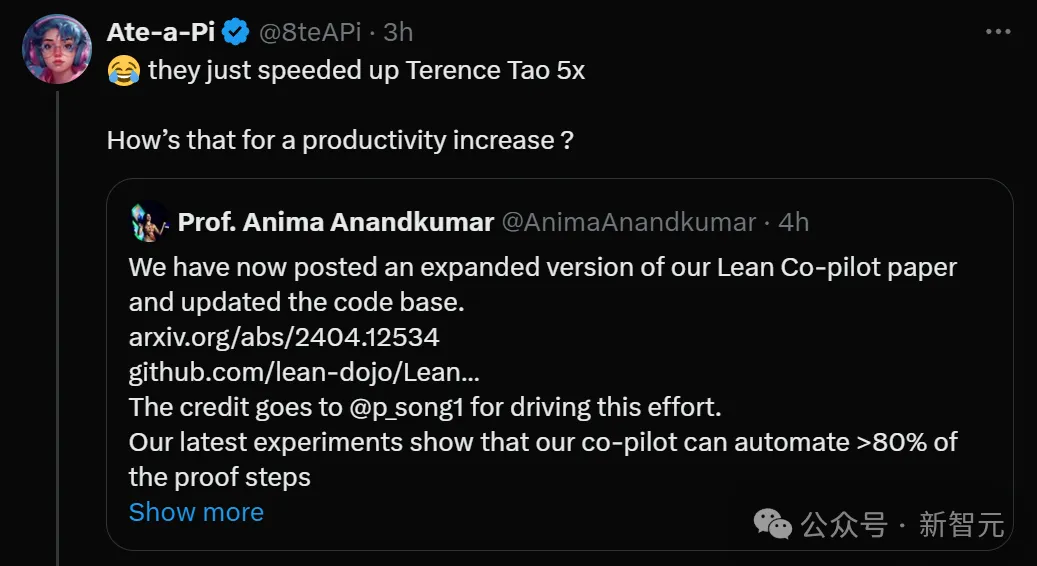
Lean Copilot, alat matematik formal yang telah dipuji oleh ramai ahli matematik seperti Terence Tao, telah berkembang semula?

Sebentar tadi, profesor Caltech Anima Anandkumar mengumumkan bahawa pasukan itu telah mengeluarkan versi diperluaskan kertas Lean Copilot dan mengemas kini pangkalan kod. . Rekod ini adalah 2.3 kali lebih baik daripada aesop garis dasar sebelumnya.

Dan, seperti sebelum ini, ia adalah sumber terbuka di bawah lesen MIT.

Pictures

Dia seorang lelaki Cina Song Peiyang Dia adalah pelajar sarjana muda CS kehormat di UCSB dan seorang penyelidik SURF di Jabatan Pengkomputeran + Sains Matematik (CMS) Institut Teknologi California.

Netizen berseru: Jadi, penyelidikan matematik Tao Zhexuan kini boleh dipercepatkan 5 kali ganda?

Pictures

LLM mencadangkan strategi pembuktian, dan manusia campur tangan dengan lancar

Pasukan mengeluarkan alat Lean Copilot ini, dengan harapan dapat memulakan kerjasama antara manusia dan LLM secara formal untuk menulis 100% secara formal.

Ia menyelesaikan cabaran teknikal teras: menjalankan inferens LLM dalam Lean.

Melalui alat ini, kami boleh membenarkan LLM mencadangkan strategi bukti dalam Lean, membolehkan manusia campur tangan dan mengubah suai dengan cara yang lancar.

Gambar

Projek ini dibangunkan kerana pembuktian teorem automatik masih menjadi cabaran yang sukar hari ini.

Kita semua tahu bahawa LLM sering melakukan kesilapan dan halusinasi apabila melakukan tugasan matematik dan penaakulan, dan sangat tidak boleh dipercayai.

Gambar

Jadi, setakat ini, bukti matematik kebanyakannya diperoleh secara manual dan memerlukan pengesahan yang teliti.

Alat pembuktian teorem seperti Lean boleh memformalkan setiap langkah proses pembuktian, tetapi memang susah untuk manusia menulis Lean.

Dalam kes ini, kelahiran Lean Copilot adalah sangat penting.

Artifak yang mengejutkan Tao Zhexuan berkali-kali: ahli matematik selesai sebelum mereka boleh menggunakannya

LLM boleh digunakan sebagai alat untuk membantu manusia dalam membuktikan teorem ini telah disahkan oleh Tao Zhexuan berkali-kali.

Dia baru saja meramalkan dalam blognya bahawa dalam 26 tahun AI akan digabungkan dengan alat carian dan matematik simbolik dan menjadi pengarang bersama yang boleh dipercayai dalam penyelidikan matematik.

Sejurus selepas itu, kajian untuk menyokong pandangannya bermunculan seperti cendawan selepas hujan.

Pada bulan Jun tahun lalu,

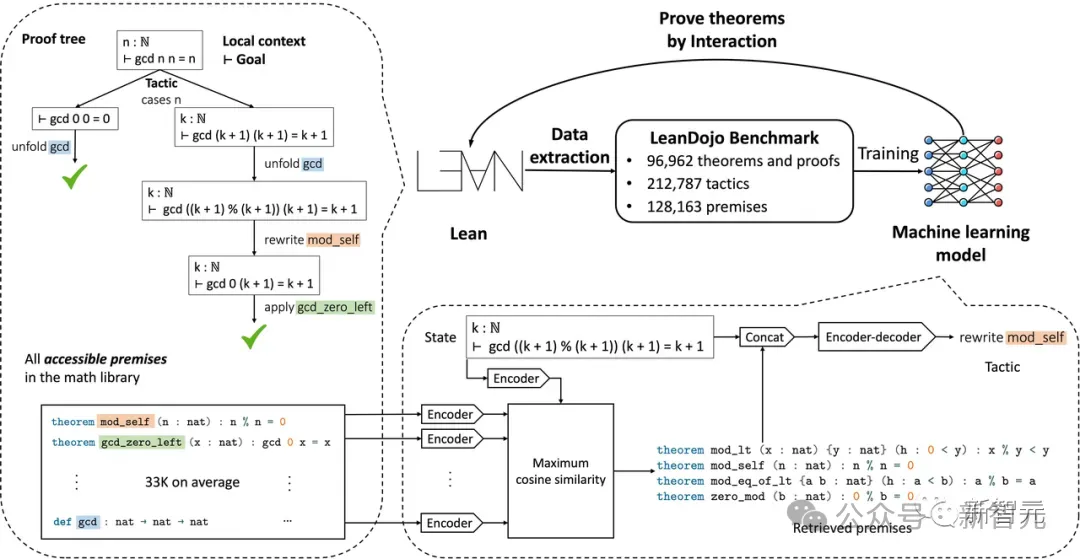
para ulama dari California Institute of Technology, NVIDIA, MIT dan institusi lain membina LeanDojo, pembukti teorem berdasarkan LLM sumber terbuka.

Gambar

Pada bulan September, penyelidik dari Microsoft Research Asia, Universiti Peking, Universiti Beihang dan institusi lain berjaya membuat GPT-4 melalui 97 pusingan penalaran yang ketat "Socratic" daripada "P≠NP" dan menyelesaikan masalah alaf ini

.

Gambar

Dalam pusingan ke-97 dialog, GPT-4 membuat kesimpulan bahawa contoh itu tidak boleh diselesaikan tanpa kaedah yang lengkap, membuktikan bahawa kesimpulannya adalah P≠NP

Oktober lalu secara langsung menemui pepijat tersembunyi dalam kertas kerjanya dengan bantuan GPT-4 dan Copilot.

Dalam proses menggunakan Lean4 untuk merasmikan hujah di muka surat 6, dia mendapati ungkapan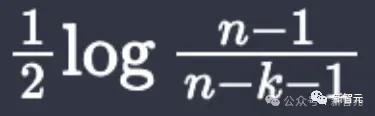

gambar

sebenarnya berbeza apabila n=3,k=2.

Pepijat yang sukar dilihat ini telah ditangkap tepat pada masanya, terima kasih kepada Lean4. Sebabnya ialah Lean memintanya membina 02. Oleh itu, Lean tidak boleh mendapatkan disproof berdasarkan negatif 0

Gambar

Penemuan ini secara langsung mengejutkan murid Tao Zhexuan. . .

GambarDalam proses ini, semua penyelidik matematik barisan hadapan telah merasakan kesan langsung AI terhadap kuasa subversif penyelidikan matematik buat kali pertama. Lean Copilot menjadikan Lean lebih baik untuk digunakan

Dan hari ini, penyelidikan oleh Lean Copilot ini telah menjadikan Lean secara langsung lebih berkuasa.

Dalam kertas kerja ini, pasukan membina alatan berdasarkan Lean Copilot untuk mencadangkan langkah pembuktian (cadangan strategi), melengkapkan matlamat pembuktian perantaraan (carian bukti), dan memilih premis yang berkaitan menggunakan LLM (pemilihan premis).

Hasil percubaan juga menunjukkan sepenuhnya bahawa berbanding dengan automasi bukti berasaskan peraturan sedia ada dalam Lean, Lean Copilot berkesan dalam membantu manusia dalam pembuktian teorem automatik.

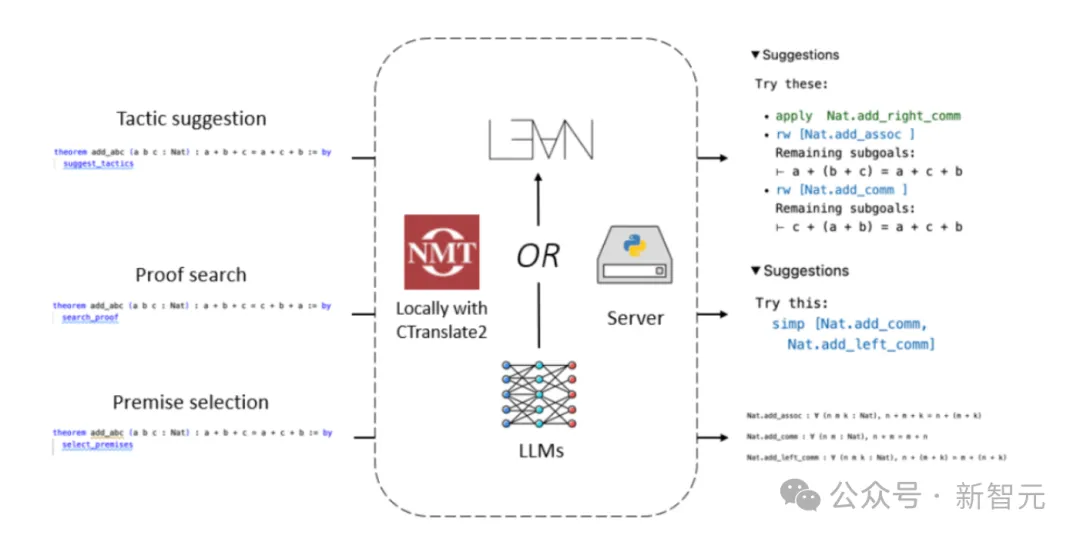
Lean Copilot menyediakan rangka kerja umum yang boleh menjalankan inferens LLM secara setempat melalui CTranslate 2, atau pada pelayan.

Melalui rangka kerja ini, pengguna boleh mencipta pelbagai alat bukti automatik.

Gambar

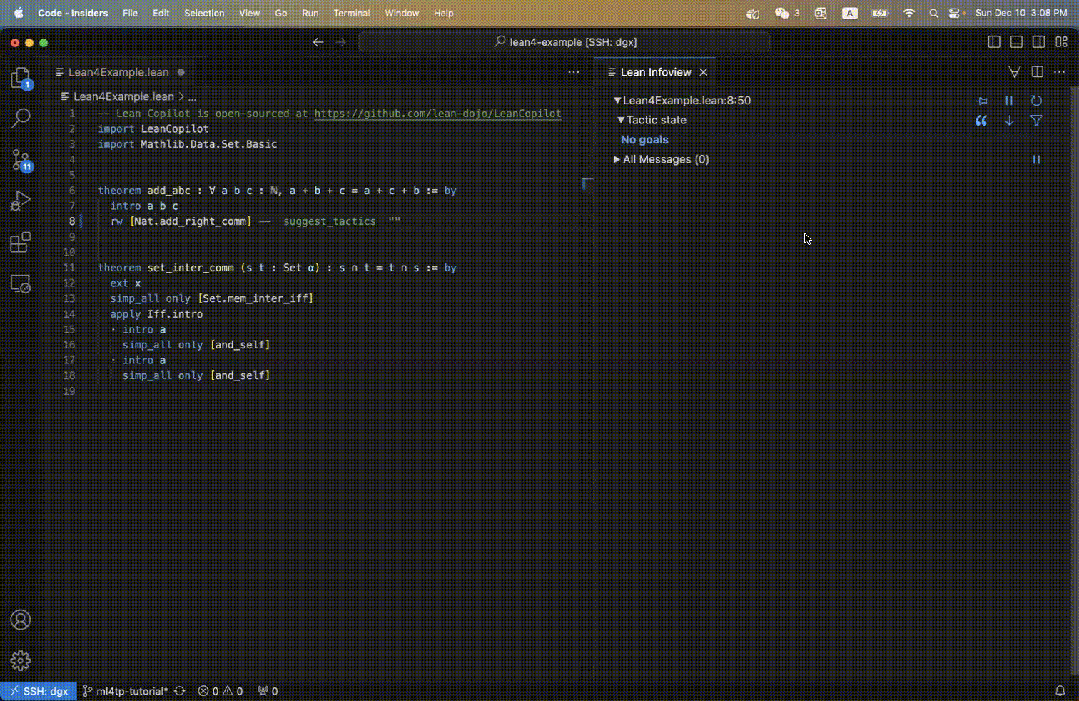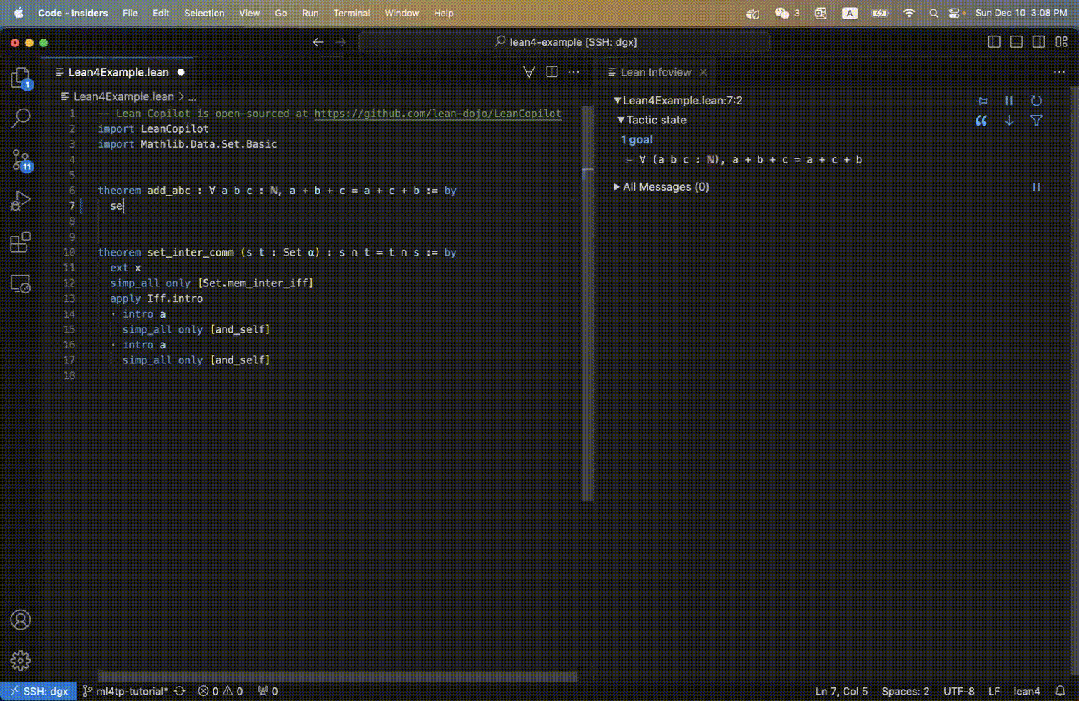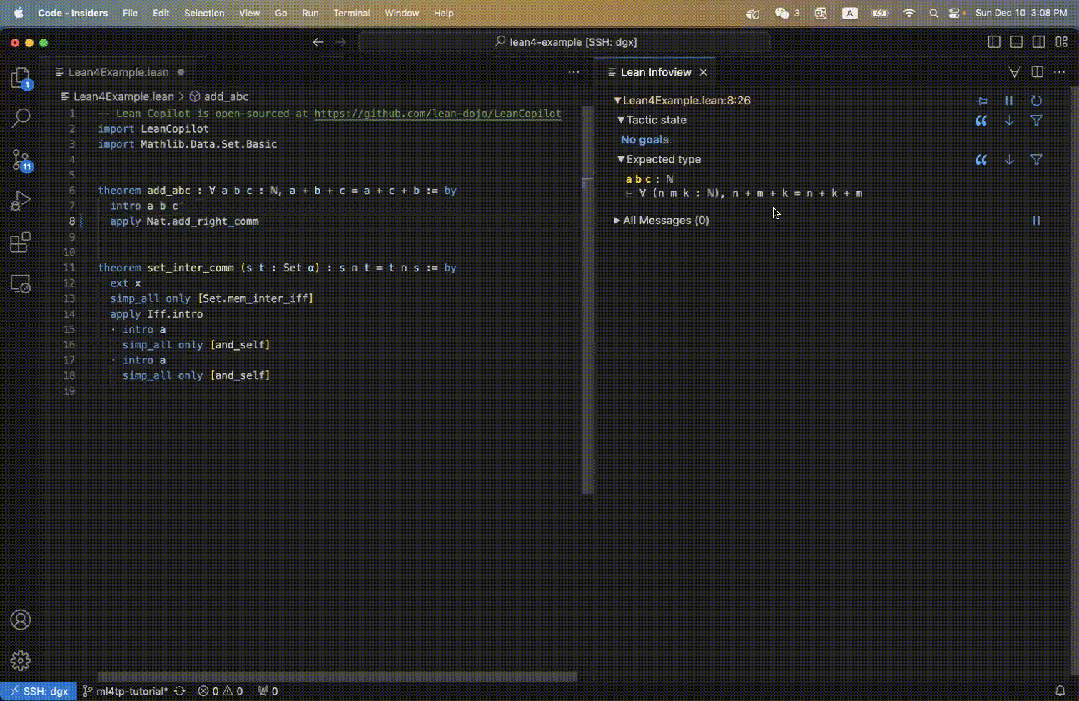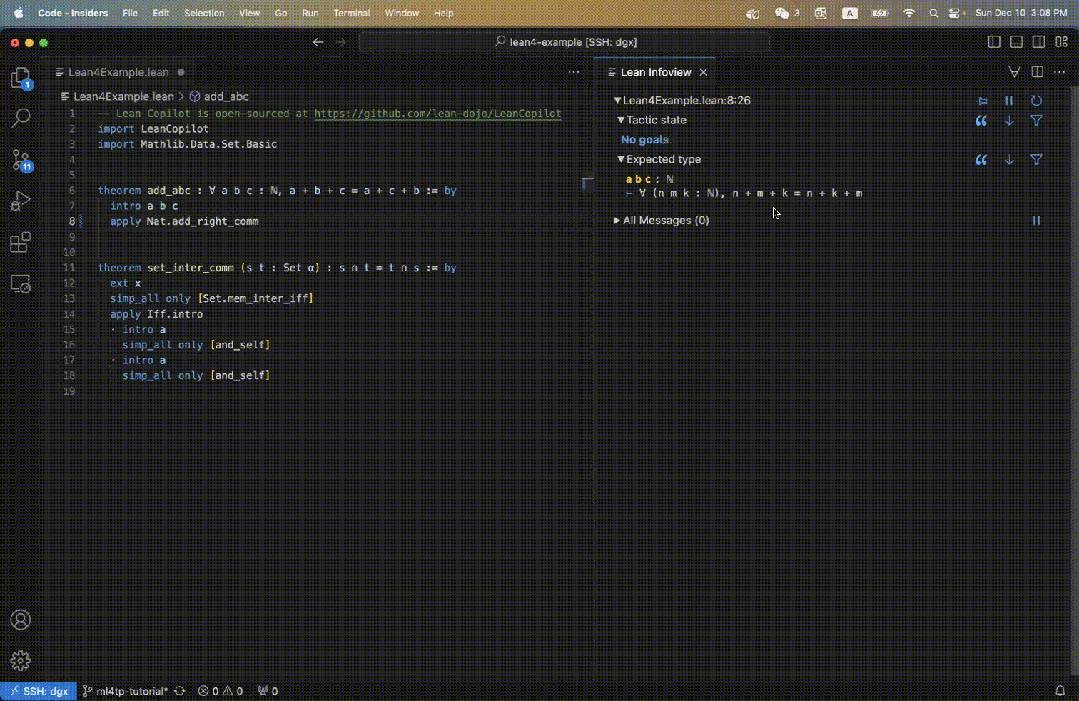
Lean ialah pembantu bukti yang sangat popular di kalangan ahli matematik. Seperti yang ditunjukkan dalam rajah di bawah, bukti dalam Lean terdiri daripada satu siri langkah pembuktian yang dipanggil taktik.

Gambar

Bermula dari keseluruhan teorem sebagai matlamat awal, strategi secara berulang mengubah matlamat semasa menjadi submatlamat yang lebih mudah sehingga semua matlamat diselesaikan.

Pengguna menulis strategi secara interaktif dalam IDE yang didorong oleh VSCode, dan matlamat dipaparkan dalam panel paparan maklumat di sebelah kanan.

Jana cadangan strategi

Menggunakan Lean Copilot, pasukan membina suggest_tropics, alat untuk menjana cadangan strategi menggunakan LLM.

Dan itu sendiri juga adalah satu strategi. Apabila

digunakan, ia memasukkan sasaran semasa ke dalam LLM dan memperoleh senarai calon dasar yang dijana daripada LLM.

Ia melihat setiap pilihan untuk melihat sama ada ia 1) mengakibatkan kesilapan;

Jika 1), strategi ini akan dipadamkan.

Gambar

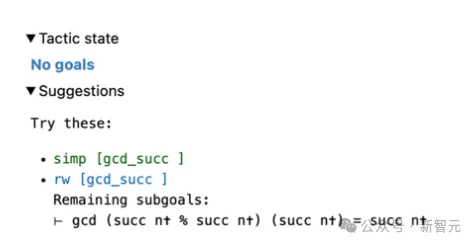
Hanya strategi bebas ralat akan dipaparkan dalam panel paparan di sebelah kanan.

Antaranya, strategi yang berjaya melengkapkan pembuktian ditanda dengan warna hijau (kategori 3);

Perhatian! Apabila semua strategi yang disenaraikan termasuk dalam Kategori 2, maklumat ini boleh menjadi sangat berharga kepada pengguna.

Dalam kes ini, maklumat matlamat yang tinggal boleh secara langsung membantu pengguna memilih strategi sebagai langkah pembuktian perantaraan seterusnya.

Selepas melihat cadangan, pengguna boleh memilih sama ada untuk menerimanya atau menggunakannya sebagai sumber inspirasi untuk membangunkan strategi baharu.

Sebagai contoh, kami mentakrifkan teorem add_abc dalam kod Lean, dan matlamat awalnya ditunjukkan di sebelah kanan Rajah 3.

Gambar

Apabila kita memasuki suggest_tropics, kita akan melihat cadangan strategi di sebelah kanan.

Strategi pertama ditunjukkan dalam warna hijau, menunjukkan bahawa bukti telah berjaya diselesaikan.

Tiga cadangan seterusnya semuanya berwarna biru, yang menunjukkan bahawa bukti tidak boleh dilengkapkan secara langsung, tetapi tidak akan membawa kepada kesilapan.

Oleh itu, ia mungkin merupakan langkah pembuktian perantaraan yang sah!

Pada masa yang sama, sub-matlamat yang selebihnya turut dipaparkan.

Medan keadaan Taktik menunjukkan Tiada matlamat kerana sekurang-kurangnya satu cadangan strategi boleh dibuktikan. .

Apabila ia datang kepada Suggest_tropics yang disebutkan di atas, ia hanya boleh menjana strategi langkah semasa dan tidak mempunyai keupayaan untuk mencari bukti pelbagai strategi.

Untuk tujuan ini, pasukan menggabungkannya dengan alat carian bukti berasaskan peraturan aesop untuk membina alat carian bukti berasaskan LLM.

Aesop akan melaksanakan carian terbaik pertama sebagai strategi Lean dan membolehkan pengguna mengkonfigurasi cara pepohon carian dikembangkan.

Gambar

Pepohon carian terdiri daripada sasaran yang merupakan nod.

Pada mulanya, ia hanya mempunyai sasaran asal sebagai nod akar. Pada setiap langkah, aesop memilih nod belum dikembangkan yang paling menjanjikan, mengembangkannya dengan menggunakan dasar dan menambah nod yang terhasil sebagai nod anak.

gambar

Dan apabila aesop menemui jalan dari punca kepada sasaran yang mudah diselesaikan, ia membuktikan bahawa pencarian itu berjaya!

Oleh itu, prestasi aesop secara kritikal bergantung pada sama ada pengguna mengkonfigurasi set peraturan yang berkesan.

Ini menunjukkan aesop kurang fleksibiliti. Oleh itu, Search_proof mempertingkatkan peraturan aesop dengan menjadikannya lebih fleksibel dengan dasar berkaitan sasaran yang dijana oleh suggest_tropics pada setiap langkah.

Untuk matlamat asal dalam Rajah 3, pengguna hanya perlu memasukkan search_prrof dan mencari bukti lengkap yang boleh menyelesaikan matlamat, yang dipaparkan dalam paparan maklumat (Rajah 5 kanan).

Anda dapat melihat bahawa sejak bukti kejayaan ditemui, keadaan Taktik yang tinggal ialah Tiada gol.

Gambar

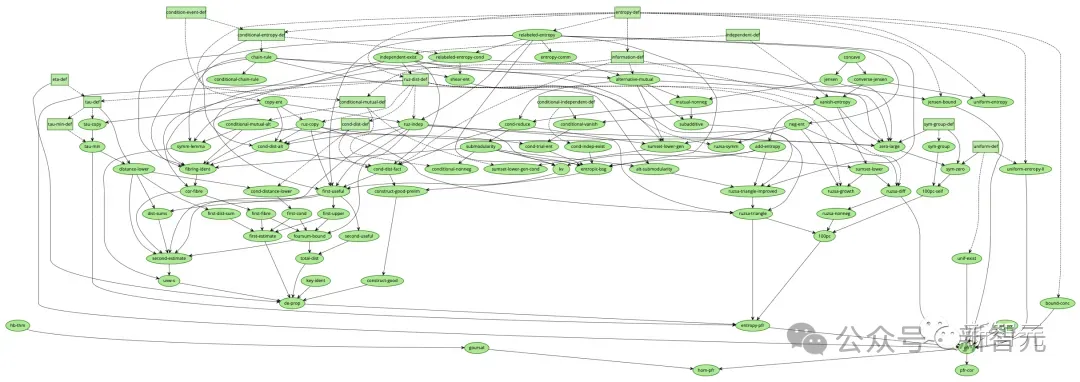
Pilih premis yang beranotasi baik

Selain itu, satu lagi tugas yang mencabar dan penting dalam pembuktian teorem ialah mencari premis yang relevan yang mengurangkan atau melengkapkan bukti.

Selain sejumlah besar prasyarat dalam perpustakaan kod sumber dan perpustakaan standard, Lean juga mempunyai perpustakaan matematik yang besar (Mathlib).

Namun, mencari premis calon dari semua perpustakaan adalah amat sukar dan memakan masa.

Sekian ramai orang cuba mendapatkan bantuan daripada Lean atau pembantu bukti lain, atau untuk mengautomasikan proses ini.

Gambar

Dalam Lean, kaedah pemilihan premis yang paling maju ialah rangka kerja berdasarkan hutan rawak (hutan rawak) yang dilaksanakan terus dalam Lean.

Walau bagaimanapun, tugas pemilihan premis sangat sesuai untuk LLM yang dipertingkatkan semula, di mana matriks perolehan (pembenaman premis) dilatih semasa latihan model besar untuk menganggarkan korelasi antara sasaran bukti dan premis calon.

Memandangkan matlamat pembuktian pada masa inferens, mula-mula mengekod matlamat menjadi vektor dan kemudian lakukan pendaraban matriks-vektor antara pembenaman premis dan vektor matlamat.

Kemudian, untuk memilih premis k teratas (di mana k boleh menjadi hiperparameter yang menentukan berapa banyak premis yang ingin dipulangkan oleh pengguna), hanya kembalikan premis k dengan markah tertinggi.

Untuk melaksanakan tugas penaakulan dalam Lean, sebagai tambahan kepada penaakulan pantas yang disediakan oleh Lean Copilot, anda juga memerlukan perpustakaan pendaraban matriks yang cekap dan pembaca matriks numpy C++.

Para penyelidik menggunakan fungsi pendaraban matriks daripada CTranslate2 dan pembaca fail numpy pantas C++ daripada Libnpy.

Mereka memautkan nombor ini kepada Lean sekali lagi melalui mekanisme FFI.

Oleh itu, strategi pemilihan premis boleh berjalan dengan sangat cekap, memandangkan pembenaman premis boleh diprakira dan semua operasi seterusnya boleh dilakukan dengan cepat dalam C++ menggunakan perpustakaan yang diperkenalkan di atas.

Setelah mendapat premis pemulangan, pengkaji seterusnya menganotasikannya dengan maklumat yang berguna.

Di sini, semua premis dibahagikan kepada dua kategori: premis yang boleh digunakan secara terus dalam persekitaran semasa (in-scope premises) dan premis yang tidak boleh digunakan secara langsung dalam persekitaran semasa (out-of-scope premises).

Ini bergantung kepada sama ada pakej yang diperlukan diimport.

Anda boleh menggunakan premis dengan mudah jika anda sudah mengimport pakej yang diperlukan oleh premis. Rajah 6 di bawah menunjukkan premis skop beranotasi.

Rajah 7 menunjukkan premis luar skop beranotasi.

Berikut adalah contoh penggunaan "premise selection". Untuk teorem add_abc dalam Rajah 3, anda boleh terus memasukkan select_premises dalam bukti (Rajah 8 kiri).

Kemudian, senarai prasyarat yang berkaitan akan muncul dalam paparan maklumat (Rajah 8, kanan).

Untuk teorem mudah ini, dapat dilihat dengan jelas bahawa premis yang dipilih sememangnya relevan, kerana semuanya berkaitan dengan nombor asli dan peraturan tambah.

Dalam kes ini, 4 premis terpilih semuanya dalam skop semasa, bermakna modul mereka sudah diimport.

Di atas ialah tiga alat automasi bukti praktikal yang dibina oleh penyelidik melalui Lean Copilot, yang digunakan untuk cadangan strategi, bukti carian dan pemilihan premis.

81.2% daripada langkah pembuktian semuanya automatik

Melalui rangka kerja Lean Copilot, penyelidik secara empirikal mengemukakan hipotesis bahawa kerjasama manusia-mesin dalam Pembuktian Teorem Interaktif Lean (ITP) adalah bermanfaat.

Disebabkan proses pembuktian teorem dalam Lean, ia tertumpu terutamanya pada pembuktian strategi.

Oleh itu, dalam eksperimen khusus, pengarang terutamanya menilai alat automasi bukti untuk "cadangan strategi" dan "carian bukti".

Ringkasnya, aesop ialah alat automasi bukti berasaskan peraturan yang paling canggih untuk carian bukti.

Para penyelidik mengesahkan keberkesanan bukti carian berasaskan LLM berbanding aesop dalam dua kes:

(1) Bukti autonomi teorem (LLM dilengkapkan secara bebas)

Perlaksanaan Assistance Manusia (2) pembuktian (manusia dan AI bekerjasama)

Selain itu, penyelidik juga membandingkan bukti carian dengan cadangan strategi untuk membuktikan kelebihan bukti carian selain cadangan strategi tunggal.

Kaji bagaimana Lean Copilot boleh membantu manusia dengan berkesan dalam proses ITP, sama seperti paradigma manusia menggunakan Copilot dalam pengaturcaraan perisian.

Maksudnya, apabila kita menghadapi matlamat, kita akan terlebih dahulu menghubungi Copilot untuk melihat sama ada ia boleh menyelesaikan masalah secara langsung.

Jika tidak, kami memudahkan lagi matlamat dan cuba Copilot lagi. Kemudian, proses di atas diulang sehingga Copilot berjaya menyelesaikan sasaran yang tinggal.

Para penyelidik menggunakan contoh kerjasama berulang ini untuk melihat berapa banyak tenaga kerja setiap alat automasi bukti boleh mengautomasikan.

Keputusan khusus ditunjukkan dalam Jadual 1 di bawah.

Carian bukti (kalis_carian) secara automatik boleh membuktikan 64% teorem (32 daripada 50), jauh lebih tinggi daripada aesop dan cadangan strategi (suggest_tropics).

Apabila digunakan untuk membantu manusia, carian bukti hanya memerlukan purata 1.02 strategi yang dimasukkan secara manual, yang juga lebih baik daripada aesop (3.62) dan cadangan strategi (2.72).

Gambar

Akhir sekali, untuk setiap teorem yang diuji, penulis mengira peratusan langkah pembuktian yang boleh diautomasikan oleh setiap tiga alat.

Hasilnya mendapati bahawa carian bukti boleh melengkapkan secara automatik kira-kira 81.2% daripada langkah pembuktian dalam teorem, yang jauh lebih tinggi daripada cadangan strategi (48.6%) dan aesop (35.2%).

Ringkasnya, prestasi carian bukti adalah 1.67 kali lebih baik daripada cadangan dasar dan 2.31 kali lebih baik daripada aesop garis dasar berasaskan peraturan.

Inferens LLM asli dalam Lean melalui Copilot

cadangan taktik, carian bukti dan pemilihan premis dalam Lean Copilot ini mungkin kelihatan berbeza, tetapi keperluan untuk pengalaman pengguna adalah serupa.

Mereka semua perlu menjana respons dengan cukup cepat, mempunyai keperluan pengiraan yang sederhana, semasa berjalan dalam Lean.

Sebab pengguna mempunyai keperluan ini adalah kerana Lean sendiri boleh memberikan maklum balas persekitaran (seperti baki sasaran, mesej ralat, maklumat taip, dll.) dengan sangat cepat dalam kebanyakan kes.

Kelajuan ini konsisten dengan intipati pembuktian teorem - ia memerlukan penaakulan yang koheren.

Jika Lean Copilot memerlukan pengguna menunggu lama, sukar untuk kerjasama antara manusia dan AI berfungsi.

Begitu juga, kami juga sangat ingin memenuhi keperluan pengkomputeran rendah. Kerana pembuktian teorem dalam Lean sendiri tidak memerlukan GPU dan boleh dijalankan pada komputer riba tempatan pengguna.

Oleh itu, adalah sangat penting bagi pengguna Lean untuk dapat berjalan dengan cekap pada kebanyakan perkakasan (termasuk komputer riba tanpa GPU).

Oleh kerana pengguna mungkin tidak mempunyai akses kepada GPU berdaya CUDA semasa menulis bukti.

Oleh kerana inferens pantas dan keperluan pengiraan yang rendah perlu dipenuhi, dan semua rangka kerja pembelajaran mendalam yang popular dan cekap adalah dalam Python, penyelesaian semula jadi yang difikirkan oleh pasukan adalah untuk mengehoskan model dalam Python (tempatan atau jauh), dan kemudian Buat permintaan kepada model daripada Lean.

Walau bagaimanapun, pendekatan ini mengalami overhed komunikasi antara proses, dan ia memerlukan pengguna melakukan langkah persediaan tambahan dan tidak sesuai untuk aliran kerja tradisional Lean.

Untuk mengatasi isu ini, Lean Copilot menjalankan LLM secara asli dalam Lean melalui Antara Muka Fungsi Asing (FFI).

FFI ialah mekanisme yang membenarkan program yang ditulis dalam satu bahasa untuk memanggil subrutin dalam bahasa lain.

Bahagian Lean dilaksanakan dalam c++ dan boleh beroperasi secara efisien dengan c++.

Pengaturcara boleh mengisytiharkan fungsi dalam Lean tetapi melaksanakan badan fungsi dalam C++. Pelaksanaan disusun ke dalam perpustakaan kongsi dan dipautkan secara dinamik kepada Lean.

Secara lalai, kami menggunakan model repver terlatih LeanDojo. Ia adalah berdasarkan penukar pengekod-penyahkod, BVT5, yang memetakan rentetan input kepada rentetan output.

Lean Copilot menjadikannya boleh dijalankan dalam Lean dengan membungkus model ke dalam fungsi C++ yang beroperasi pada rentetan, yang boleh dipanggil dalam Lean melalui FFI.

Gambar

Pengarang Cina telah memberikan sumbangan besar

Pasukan tiga orang dalam kertas terbaru juga merupakan pengarang platform sumber terbuka LeanDojo pada 23 Jun.

Gambar

Alamat kertas: https://arxiv.org/pdf/2306.15626.pdf

Lagu Peiyang🜎🜎🜎 Gambar

Lagu Peiyang ialah pelajar sarjana muda Kepujian dalam Sains Komputer di Kolej Pengajian Kreatif (CCS) di UC Santa Barbara, dibimbing oleh Richert Wang dan Phill Conrad.

Pada masa yang sama, beliau juga merupakan penyelidik SURF di Jabatan Sains Pengiraan dan Matematik (CMS) di Caltech, diselia bersama oleh Profesor Anima Anandkumar dan Dr Kaiyu Yang.

Pictures

Selain itu, beliau ialah penyelidik di Makmal Seni Bina UC Berkeley, bekerja dengan Tim Sherwood dan Dr. Jeremy Lau (Google).

Minat penyelidikannya ialah pembelajaran mesin (ML), melibatkan bidang aplikasi seperti pemprosesan bahasa semula jadi (NLP) dan penglihatan komputer (CV), serta teori asas seperti sistem dan bahasa pengaturcaraan (PL).

Penyelidikan terbaru Song Peiyang mempunyai dua hala tuju.

Satunya ialah Neural Symbolic Reasoning dan Artificial Intelligence Mathematics (AI4Math), yang menggabungkan model besar dengan provers teorem interaktif (ITP).

Yang lain ialah pembelajaran mesin cekap tenaga berdasarkan logik temporal. Kaiyu Yang (杨凯媪)

Beliau menerima PhD dari Princeton University, di mana penyelianya ialah Jia Deng, dan dia juga bekerja dengan Olga Russakovsky dan Chen Danqi.

Penyelidikannya memfokuskan pada kecerdasan buatan neurosimbolik, yang bertujuan untuk membolehkan pembelajaran mesin melakukan penaakulan simbolik, dengan harapan dapat mencapai ini melalui dua arah:

(1) Mengaplikasikan pembelajaran mesin kepada tugas penaakulan simbolik, seperti logik formal Atau penaakulan dan teorem matematik dalam bahasa semula jadi;

(2) Memperkenalkan komponen simbolik ke dalam model pembelajaran mesin untuk menjadikannya lebih mudah ditafsir, boleh disahkan dan cekap data.

Pada masa ini, dia sedang mengusahakan kecerdasan buatan yang boleh memahami dan menaakul tentang matematik. Penaakulan matematik ialah peristiwa penting dalam kecerdasan manusia dan berpotensi untuk mengubah banyak masalah penting dalam sains dan kejuruteraan, seperti menyelesaikan persamaan pembezaan separa dan pengesahan formula.

Anima Anandkumar

Anima Anandkumar kini seorang profesor sains pengiraan dan matematik di Caltech.

Gambar

Minat penyelidikannya tertumpu terutamanya pada bidang pembelajaran mesin berskala besar, pengoptimuman bukan cembung dan statistik berdimensi tinggi.

Secara khususnya, beliau telah menerajui pembangunan dan analisis algoritma tensor untuk pembelajaran mesin.

Kaedah penguraian tensor mempunyai keselarian dan kebolehskalaan yang sangat tinggi dan boleh digunakan pada data besar-besaran. Ia boleh menjamin penumpuan kepada penyelesaian optimum dan menghasilkan keputusan anggaran yang konsisten untuk banyak model kebarangkalian (seperti model Markov).

Secara lebih meluas, Profesor Anandkumar telah meneliti teknik yang cekap untuk mempercepatkan pengoptimuman bukan cembung.

Rujukan:

https://www.php.cn/link/1dd5a4016c624ef51f0542d4ae60e281

7d f6e79b0be391f720e4

https ://www.php.cn/link/a652e914c736dfaf8a6667ae6936f0d6

Atas ialah kandungan terperinci Caltech Cina menggunakan AI untuk menumbangkan bukti matematik! Mempercepatkan 5 kali terkejut Tao Zhexuan, 80% langkah matematik adalah automatik sepenuhnya. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!