Satu kejayaan baharu telah dibuat dalam masalah pemotongan minimum graf tidak terarah dan penyelidikan Google memenangi Anugerah Kertas Terbaik SODA 2024

Blog Google mengeluarkan penyelidikan baharu untuk menyelesaikan masalah pemotongan minimum bagi graf tidak terarah.

Pada tahun 1996, saintis komputer Amerika David R Karger dan penyelidik lain mencadangkan algoritma rawak yang mengejutkan Algoritma Karger dalam kertas "Pendekatan baru untuk masalah potongan minimum", yang sangat popular dalam sains komputer teori sangat penting, terutamanya sesuai untuk anggaran masalah pemotongan minimum pada graf berskala besar.

Algoritma Karger boleh mencari titik potong minimum dalam graf dalam masa O (m log^3n), yang mereka panggil masa hampir linear, bermaksud pendaraban linear dengan faktor polilogaritma.

Dalam blog yang baru dikemas kini oleh Google, mereka memperkenalkan kertas kerja "Deterministic Near-Linear Time Minimum Cut in Weighted Graphs", dan penyelidikan itu memenangi Anugerah Kertas Terbaik ACM-SIAM SODA24. Artikel ini memperincikan algoritma baharu yang berjalan dalam masa hampir linear (bukannya mendekati masa linear). Algoritma ini bersifat deterministik dan boleh mencari potongan minimum yang betul Algoritma untuk graf mudah. Boleh dikatakan ini adalah penemuan terbesar sejak algoritma rawak terkenal Karger. .

Nota: terkecil Masalah pemotongan (selalunya dipanggil potongan minimum) ialah masalah struktur asas mengenai ketersambungan graf Ia secara amnya memfokuskan pada apakah cara paling mudah untuk memutuskan sambungan rangkaian? Dalam teori graf, set tepi yang boleh membuat graf aliran rangkaian tidak lagi bersambung (iaitu, dibahagikan kepada dua subgraf) dengan mengeluarkan semua tepi dipanggil potongan graf, dan potongan terkecil pada graf dipanggil a potongan minimum.

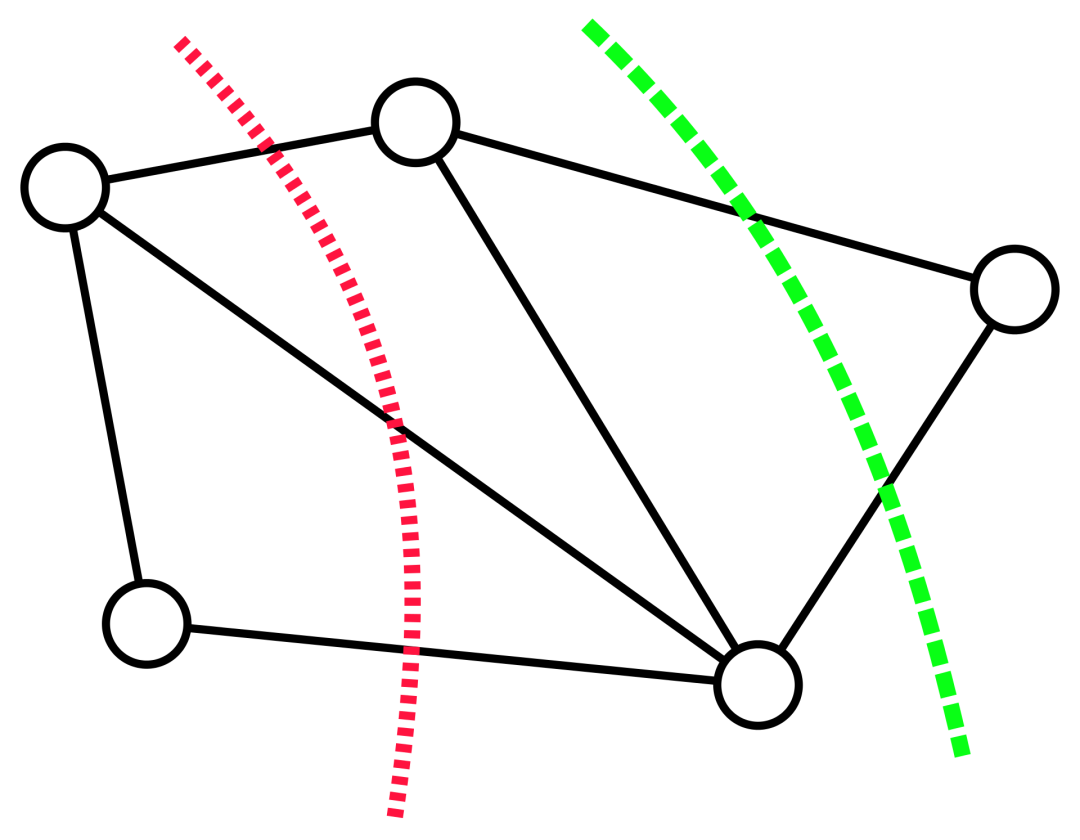
•                                                                                                                                                                                                                                                                                                                                 Graf dan dua potongannya: garis putus-putus merah menandakan potongan yang mengandungi tiga tepi dan garis putus-putus hijau mewakili potongan minimum (termasuk dua tepi) graf ini.

Pengenalan kaedah

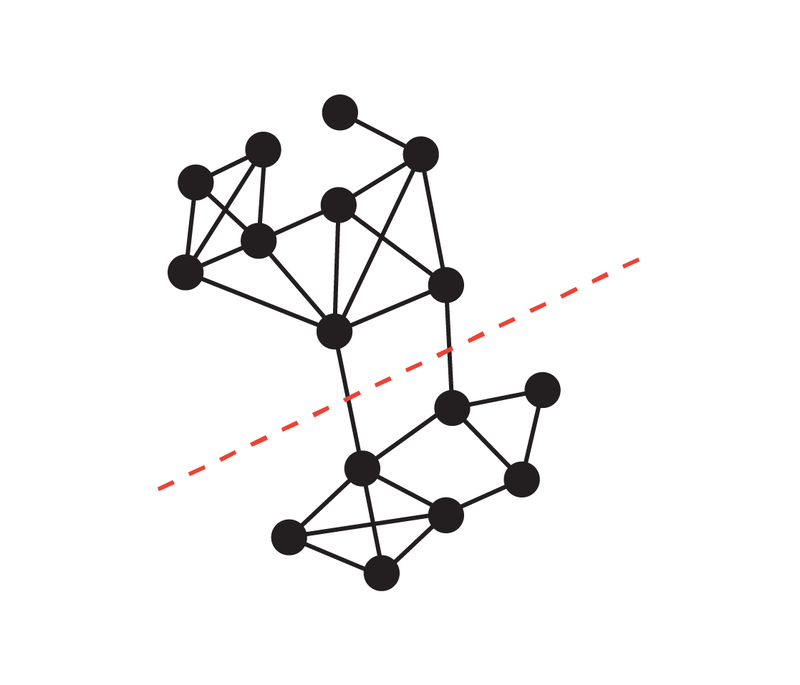
Berkenaan masalah pemotongan minimum, Karger mempelopori algoritma rawak masa hampir linear pada tahun 1996, yang boleh mencari pemotongan kebarangkalian kerja yang tinggi. cerapan utama bahawa terdapat graf yang lebih kecil yang sebahagian besarnya mengekalkan saiz semua potongan.

Penemuan ini berguna kerana algoritma yang lebih perlahan boleh dijalankan menggunakan graf yang lebih kecil sebagai input, dan masa berjalan yang lebih perlahan (dari segi saiz graf yang lebih kecil) masih setanding dengan yang asal ( Lebih Besar) Saiz graf graf hampir linear.

Sebenarnya, banyak penemuan struktur mengenai masalah pemotongan minimum dilakukan di sepanjang arah ini.

Google melakukan ini, bermula daripada graf G dengan n nod, dan kemudian berdasarkan kaedah sparsifikasi pengawetan potong yang dicadangkan dalam kertas "Skim Penghampiran Rawak untuk Pemotongan dan Aliran dalam Graf Berkapasiti" (dikarang oleh Benzur, Karger ), membuktikan bahawa graf berwajaran jarang G' dengan tepi yang lebih sedikit boleh dibina, dan pada graf ini, saiz hampir semua potongan adalah lebih kurang sama dengan saiz potongan sepadan dalam graf asal G.

Konsep ini boleh digambarkan melalui contoh berikut: graf asal terdiri daripada dua graf lengkap yang disambungkan oleh satu tepi, manakala graf terpencar mempunyai lebih sedikit tepi, tetapi berat tepinya lebih besar, dan pada masa yang sama masa semua pemotongan Saiznya dipelihara secara kasar.

Untuk membina graf yang lebih jarang ini, Benzur dan Karger menggunakan kaedah persampelan tepi secara bebas. Dalam kaedah ini, setiap tepi dalam graf G mempunyai kebarangkalian tertentu untuk dimasukkan ke dalam graf G', dan beratnya dalam G' akan dikuatkan mengikut songsangan kebarangkalian pensampelan (contohnya, jika berat asal tepi ialah 1 Tepi disertakan dengan kebarangkalian 10%, kemudian beratnya dilaraskan kepada 10). Ternyata kaedah yang sangat mudah (hampir masa linear) ini boleh membina pemisahan graf pemeliharaan potong dengan kebarangkalian kejayaan yang tinggi.

Walau bagaimanapun, algoritma Karger ialah algoritma Monte Carlo, iaitu output mungkin tidak betul dengan kebarangkalian kecil, dan tiada cara yang diketahui untuk mengetahui sama ada output itu betul selain membandingkannya dengan potongan minimum yang diketahui sebenar. .

Oleh itu, penyelidik telah berusaha keras untuk meneroka cara untuk menyelesaikan masalah terbuka algoritma penentuan masa hampir linear. Memandangkan pembinaan pemisahan graf pemuliharaan potong adalah satu-satunya komponen stokastik algoritma Karger, satu pendekatan adalah untuk mencari pembinaan penentuan pemisahan dalam masa hampir linear (juga dipanggil derandomisasi).

Pada tahun 2015, Kawarabayashi dan Thorup mencapai pencapaian penting - mencari algoritma masa hampir linear deterministik untuk graf mudah (iaitu, graf dengan paling banyak satu tepi antara setiap pasangan nod dan semua pemberat tepi bersamaan dengan 1) .

Kajian ini membawa kepada idea utama, iaitu, terdapat beberapa perkaitan antara potongan minimum dan satu lagi struktur graf penting (dipanggil "potongan konduktans rendah"). Sambungan ini adalah penting untuk mengubah dominasi algoritma Karger pada graf berwajaran tepi umum kemudiannya dan membantu Google memperoleh algoritma baharunya.

Penjajaran potongan minimum dan potongan konduktans rendah

Konduktans potongan graf S ditakrifkan sebagai nisbah saiz potongan S kepada isipadu S (dengan andaian S ialah sisi volum yang lebih kecil pada potongan dan tidak kosong), di mana isipadu S ialah darjah nod dalam S.

konduktans rendah potongan S secara intuitif menangkap kesesakan dalam rangkaian, kerana terdapat hanya sebilangan kecil tepi (berbanding dengan isipadunya) yang menyambungkan S ke seluruh graf. Konduktans graf ditakrifkan sebagai konduktans minimum untuk sebarang potongan dalam graf, dan graf dengan konduktans besar (juga dipanggil graf lanjutan) dikatakan bersambung dengan baik kerana tiada halangan di dalamnya. Garis putus-putus merah menunjukkan bahawa saiz CUT ialah 2, dan sisi yang lebih kecil (bawah) Isipadu ialah 24, jadi Konduktansnya ialah 1/12, yang juga merupakan Konduktansi graf.

^{Kawayabarashi dan Thorup memerhatikan bahawa dalam graf mudah dengan darjah nod minimum yang besar, sebarang potongan minimum bukan remeh (iaitu sekurang-kurangnya dua nod pada kedua-dua belah) mesti mempunyai konduktans yang rendah. Berdasarkan pemerhatian ini, jika graf boleh dibahagikan kepada gugusan yang bersambung dengan baik, maka pembahagian mestilah konsisten dengan setiap potongan min bukan remeh, kerana setiap gugusan mesti terletak tepat pada satu sisi setiap potongan. Kemudian, setiap kelompok dikecilkan kepada nod dan graf yang lebih kecil diproses di mana semua potongan minimum bukan remeh bagi graf asal adalah utuh.}

Walau bagaimanapun, untuk graf berwajaran, pemerhatian di atas tidak lagi berlaku, dan pembahagian yang sama yang digunakan dalam kes graf ringkas mungkin tidak betul-betul konsisten dengan pemotongan minimum bukan remeh.

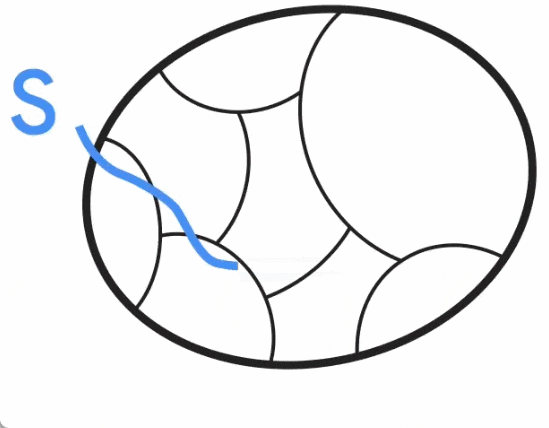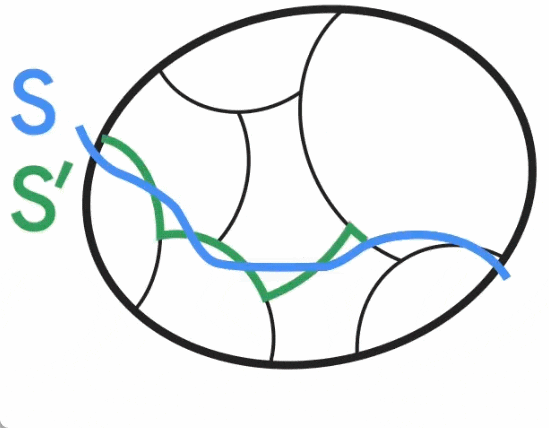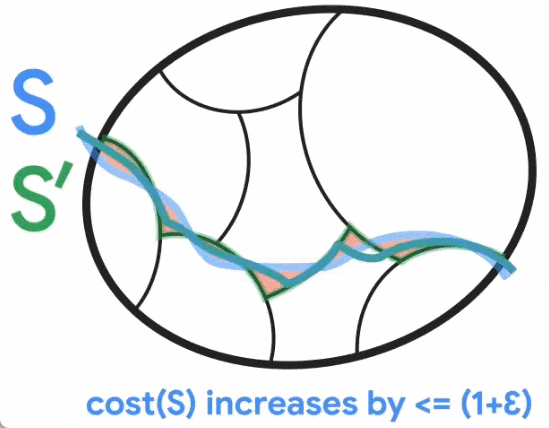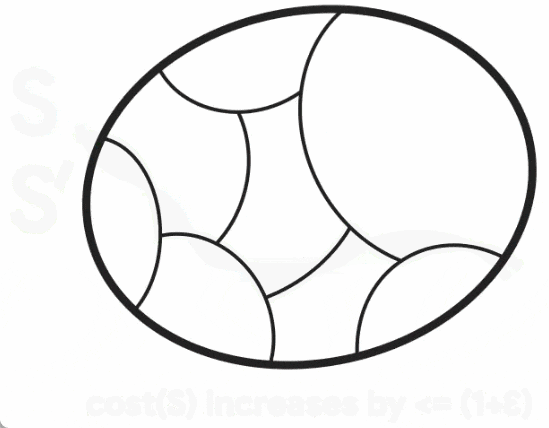
Seperti yang ditunjukkan dalam rajah di bawah, Jason Li memerhatikan pada 2021 bahawa pembahagian ini masih kira-kira konsisten dengan pemotongan minimum yang tidak remeh. Khususnya, untuk potongan minimum S yang bukan remeh, terdapat potongan S' yang serupa dengan S supaya S' konsisten dengan kelompok. Jason Li selanjutnya memerhatikan bahawa sifat pembahagian ini boleh dieksploitasi untuk merosak secara berkesan pembinaan keterlanjuran graf pemeliharaan potong.

Algoritma baharu yang direka oleh Google bertujuan untuk membina partition untuk merumuskan kes penggunaan potongan min. Kajian Google adalah lebih tepat dan lebih pantas daripada kaedah yang lebih umum dan luar biasa yang digunakan Jason Li dalam kerja sebelumnya. Penyelidikan baharu ini mengoptimumkan masa berjalan sambil memastikan ketepatan, dan akhirnya mencapai algoritma penentu masa hampir linear untuk masalah pemotongan minimum.

Pautan rujukan: https://research.google/blog/solving-the-minimum-cut-problem-for-undirected-graphs/

Atas ialah kandungan terperinci Satu kejayaan baharu telah dibuat dalam masalah pemotongan minimum graf tidak terarah dan penyelidikan Google memenangi Anugerah Kertas Terbaik SODA 2024. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!