Butiran kerja AIOps Microsoft didedahkan

Pengenalan

Pengukuran dinamik, data ini terbahagi terutamanya kepada dua kategori: data siri masa dan data peristiwa. Data siri masa merujuk kepada siri masa bernilai sebenar (biasanya dengan selang masa tetap), seperti penggunaan CPU, dsb. manakala data peristiwa merujuk kepada jujukan yang merekodkan kejadian tertentu, seperti peristiwa limpahan memori. Untuk memastikan kualiti perkhidmatan produk, mengurangkan masa berhenti perkhidmatan, dan mengelakkan kerugian ekonomi yang lebih besar, diagnosis peristiwa perkhidmatan penting adalah amat penting. Dalam operasi sebenar dan kerja penyelenggaraan, apabila mendiagnosis peristiwa perkhidmatan, kakitangan operasi dan penyelenggaraan boleh menganalisis data siri masa yang berkaitan dengan acara perkhidmatan untuk menganalisis punca kejadian. Walaupun korelasi ini tidak dapat menggambarkan dengan tepat hubungan sebab-akibat yang sebenar, ia masih boleh memberikan beberapa petunjuk dan pendedahan yang baik untuk diagnosis.

Maka persoalannya ialah, bagaimana untuk menentukan secara automatik hubungan antara peristiwa dan data siri masa?

Soalan

Dalam artikel ini, penulis mengubah masalah korelasi data peristiwa (E) dan siri masa (S) kepada masalah dua sampel, dan menggunakan kaedah jiran terdekat untuk menentukan sama ada ia berkaitan. Terutamanya menjawab tiga soalan:A. Adakah terdapat korelasi antara E dan S? B． Jika terdapat korelasi, apakah susunan kronologi E dan S? E berlaku dahulu, atau S berlaku dahulu? C． Hubungan monotonik antara E dan S. Dengan mengandaikan bahawa S (atau E) berlaku dahulu, adakah peningkatan atau penurunan S menyebabkan E berlaku? Seperti yang ditunjukkan dalam rajah, acara adalah menjalankan program A dan B, dan data pemasaan ialah penggunaan CPU. Ia boleh didapati bahawa terdapat korelasi antara acara (menjalankan program A) dan data pemasaan (penggunaan CPU), dan ia adalah perubahan dalam penggunaan CPU yang meningkat selepas program A dijalankan.

Kaedah

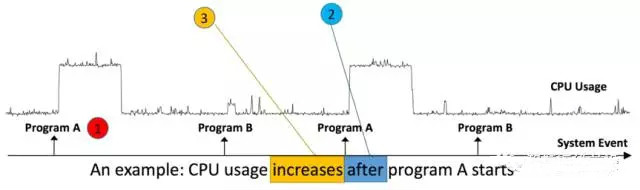
Seni bina algoritma artikel terbahagi terutamanya kepada tiga bahagian untuk menyelesaikan tiga masalah korelasi, urutan masa dan monotonisitas masing-masing. Ketiga-tiga bahagian ini akan diperkenalkan secara terperinci seterusnya.

Perkaitan

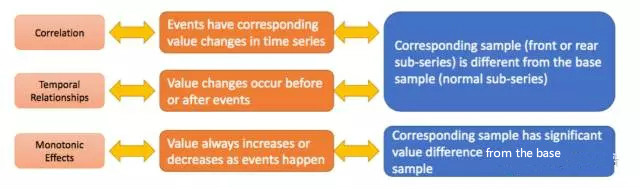
Artikel tersebut mengubah pertimbangan korelasi kepada masalah dua sampel Teras ujian hipotesis dua sampel adalah untuk menentukan sama ada kedua-dua sampel itu datang daripada pengedaran yang sama. Mula-mula, pilih N segmen data sampel siri masa dengan panjang k sepadan sebelum (atau selepas) peristiwa, diwakili oleh A1. Kumpulan sampel A2 secara rawak memilih satu siri data sampel dengan panjang k daripada siri masa. Set sampel ialah A1 dan naik ke A2. Jika E dan S adalah berkaitan, maka taburan A1 dan A2 adalah berbeza, jika tidak taburan adalah sama. Bagaimana untuk menentukan sama ada taburan A1 dan A2 adalah sama? Mari lihat contoh berikut:

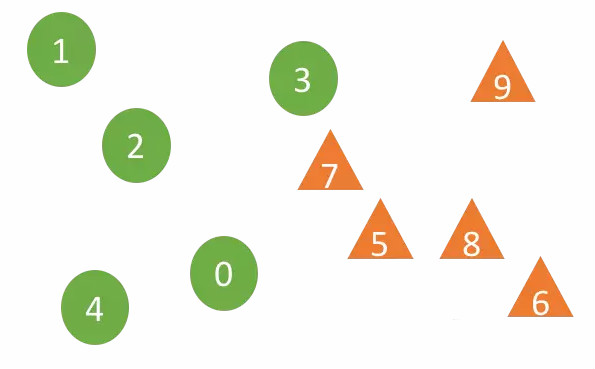
Dalam gambar di atas, sampel 0-4 adalah daripada kumpulan sampel A1, dan 5-9 tergolong dalam kumpulan sampel A2 Algoritma DTW digunakan untuk mengira jarak antara dua sampel (algoritma DTW boleh menyesuaikan dengan pengembangan dan anjakan data jujukan). Bagi sampel X kepunyaan kumpulan sampel Ai (i=1 atau 2), bagi r sampel jiran terdekat E dan S adalah lebih berkaitan. Sebagai contoh, jika bilangan jiran ialah r=2, dua jiran terdekat bagi sampel 7 ialah 3 dan 5 daripada dua kumpulan sampel yang berbeza, tetapi dua jiran terdekat bagi sampel 5 ialah 7 dan 8 daripada kumpulan sampel yang sama A2. Artikel tersebut menggunakan pekali keyakinan (Confident coefficient) untuk menilai kredibiliti "ujian hipotesis H1" (kedua-dua taburan itu tidak sama, iaitu, E dan S adalah berkaitan Semakin besar pekali keyakinan, semakin banyak). H1 yang boleh dipercayai ialah. Terdapat dua parameter utama algoritma: bilangan jiran terdekat r dan panjang siri masa k Bilangan jiran ialah logaritma semula jadi bagi bilangan sampel Puncak pertama keluk fungsi autokorelasi data siri masa ialah panjang urutan.

Jujukan masa

Pilih urutan sebelum dan selepas acara dan siri masa yang dipilih secara rawak untuk mengira korelasi. Jika Dr Betul dan Df Salah, bermakna E berlaku sebelum S berlaku (E -> S). Jika Dr adalah Salah dan Df adalah Benar, atau Dr adalah Benar dan Df adalah Benar, ia bermakna S berlaku sebelum E berlaku (S -> E). Seperti yang ditunjukkan dalam contoh di bawah, acara CPU Intensive Program -> data siri masa Penggunaan CPU, data siri masa Penggunaan CPU ->

Hubungan monotonik

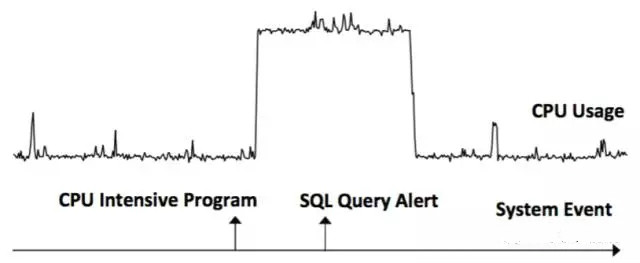
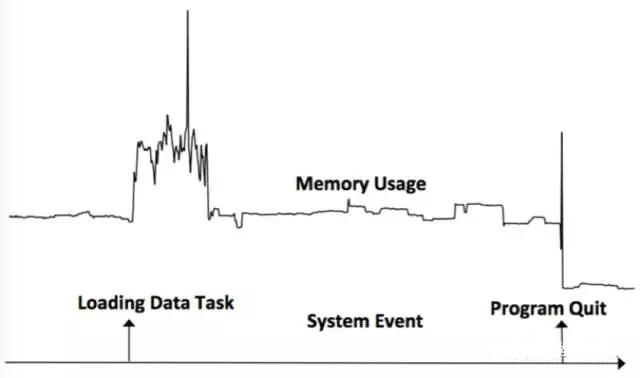
Kemonotoni dinilai berdasarkan perubahan dalam siri masa sebelum dan selepas peristiwa berlaku Jika siri masa selepas peristiwa berlaku adalah lebih besar daripada nilai urutan sebelumnya, kemonotonan akan meningkat, jika tidak, ia akan berkurangan. Seperti yang ditunjukkan dalam rajah di bawah, peristiwa memuatkan Tugas Data menyebabkan peningkatan dalam Penggunaan Memori, dan acara Program Keluar menyebabkan penurunan dalam Penggunaan Memori.

Hasil eksperimen

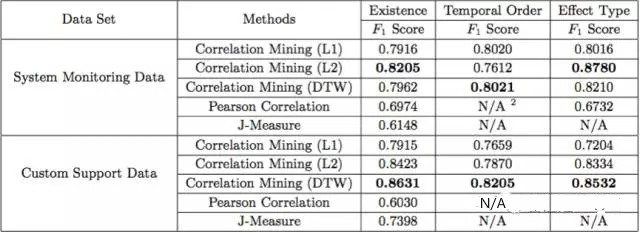
Artikel itu mengesahkan prestasi algoritma dengan menggunakan data pemantauan sistem Microsoft dan data daripada pasukan perkhidmatan pelanggan Data tersebut ialah 24 S (memori, data CPU dan CAKERA) dan 52 E (pelaksanaan tugasan tertentu), 7 S (HTTP. Kod status) dan 57 E (topik perkhidmatan), standard penilaian ialah skor F. Keputusan menunjukkan bahawa jarak DTW menunjukkan prestasi yang lebih baik secara keseluruhan daripada jarak lain (L1 dan L2), dan algoritma keseluruhan menunjukkan prestasi yang lebih baik daripada dua algoritma garis dasar (korelasi Pearson dan J-Measure).

Kesimpulan

Artikel itu memperkenalkan kaedah baharu tanpa pengawasan untuk mengkaji hubungan antara peristiwa dan data siri masa, menjawab tiga soalan: Adakah E dan S berkaitan? Dalam susunan yang manakah E dan S berlaku? Dan apakah hubungan monotonik? Berbanding dengan banyak kajian korelasi semasa, yang tertumpu terutamanya pada korelasi antara peristiwa dan korelasi antara data siri masa, artikel ini memberi tumpuan kepada hubungan antara peristiwa dan data siri masa. Ia adalah yang pertama menjawab tiga soalan di atas antara peristiwa dan masa kerja masalah siri.

Diagnosis peristiwa sentiasa menjadi tugas yang sangat penting dalam bidang operasi dan penyelenggaraan Kolerasi antara peristiwa dan data siri masa bukan sahaja dapat memberikan inspirasi yang baik untuk diagnosis peristiwa, tetapi juga memberikan petunjuk yang baik untuk analisis punca. Pengarang mengesahkan algoritma pada set data dalaman Microsoft dan mencapai keputusan yang baik, yang bernilai tinggi kepada kedua-dua kalangan akademik dan industri.

Atas ialah kandungan terperinci Butiran kerja AIOps Microsoft didedahkan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!