
Peraturan rantai terbitan ialah salah satu alat matematik penting dalam pembelajaran mesin. Ia digunakan secara meluas dalam algoritma seperti regresi linear, regresi logistik, dan rangkaian saraf. Peraturan ini ialah aplikasi peraturan rantai dalam kalkulus dan membantu kita mengira terbitan fungsi berkenaan dengan pembolehubah.
Fungsi komposit f(x) terdiri daripada berbilang fungsi ringkas, dan setiap fungsi ringkas mempunyai terbitan berkenaan dengan x. Mengikut peraturan rantai, terbitan f(x) berkenaan dengan x boleh diperolehi dengan mendarab dan menambah terbitan bagi fungsi mudah.
Ungkapan formal ialah: jika y=f(u) dan u=g(x), maka terbitan y berkenaan dengan x dy/dx=f'(u)*g'(x).
Formula ini menunjukkan bahawa dengan mengetahui terbitan fungsi mudah berkenaan dengan x dan bagaimana ia digabungkan, kita boleh mengira terbitan fungsi komposit berkenaan dengan x.
Peraturan rantai terbitan memainkan peranan penting dalam algoritma pengoptimuman, terutamanya dalam algoritma pengoptimuman seperti keturunan kecerunan. Ia digunakan untuk mengemas kini parameter model untuk meminimumkan fungsi kehilangan. Idea teras peraturan rantai ialah jika fungsi terdiri daripada berbilang fungsi mudah, maka terbitan fungsi ini berkenaan dengan pembolehubah boleh diperolehi dengan mendarabkan terbitan setiap fungsi ringkas berkenaan dengan pembolehubah. Dalam pembelajaran mesin, peraturan ini digunakan secara meluas untuk mengira kecerunan fungsi kehilangan berkenaan dengan parameter model. Keberkesanan pendekatan ini membolehkan kami melatih rangkaian saraf dalam dengan cekap melalui algoritma perambatan balik.
Dalam pembelajaran mesin, kita selalunya perlu mengoptimumkan parameter, yang melibatkan penyelesaian derivatif fungsi kehilangan berkenaan dengan parameter. Fungsi kehilangan biasanya merupakan fungsi komposit yang terdiri daripada berbilang fungsi mudah, jadi kita perlu menggunakan peraturan rantai untuk mengira derivatif fungsi kehilangan berkenaan dengan parameter.
Katakan kita mempunyai model regresi linear yang mudah Keluaran y model ialah gabungan linear input x, iaitu, y=Wx+b, di mana W dan b ialah parameter model. Jika kita mempunyai fungsi kehilangan L(y,t), dengan t ialah label sebenar, kita boleh mengira kecerunan fungsi kehilangan berkenaan dengan parameter model melalui peraturan rantai:
dL/dW=dL/ dy*dy/dW
dL/db=dL/dy*dy/db
di mana, dL/dy ialah terbitan bagi fungsi kehilangan kepada output, dy/dW dan dy/db ialah derivatif daripada output model kepada parameter. Melalui formula ini, kita boleh mengira kecerunan fungsi kehilangan pada parameter model, dan kemudian menggunakan algoritma pengoptimuman seperti keturunan kecerunan untuk mengemas kini parameter model untuk meminimumkan fungsi kehilangan.
Dalam model yang lebih kompleks, seperti rangkaian saraf, peraturan rantai juga digunakan secara meluas. Rangkaian saraf biasanya terdiri daripada berbilang lapisan tak linear dan linear, masing-masing mempunyai parameter tersendiri. Untuk mengoptimumkan parameter model untuk meminimumkan fungsi kehilangan, kita perlu mengira kecerunan fungsi kehilangan untuk setiap parameter menggunakan peraturan rantai.
Ringkasnya, peraturan rantaian terbitan ialah salah satu alat matematik yang sangat penting dalam pembelajaran mesin Ia boleh membantu kita mengira terbitan fungsi komposit berkenaan dengan pembolehubah tertentu, dan kemudian menggunakannya untuk mengoptimumkan parameter bagi. model untuk meminimumkan fungsi kehilangan.
Atas ialah kandungan terperinci Peraturan derivasi rantaian dalam pembelajaran mesin. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Let's Dance: Gerakan berstruktur untuk menyempurnakan jaring saraf manusia kitaApr 27, 2025 am 11:09 AM
Let's Dance: Gerakan berstruktur untuk menyempurnakan jaring saraf manusia kitaApr 27, 2025 am 11:09 AMPara saintis telah mengkaji secara meluas rangkaian saraf manusia dan mudah (seperti yang ada di C. elegans) untuk memahami fungsi mereka. Walau bagaimanapun, soalan penting timbul: Bagaimana kita menyesuaikan rangkaian saraf kita sendiri untuk berfungsi dengan berkesan bersama -sama dengan novel AI s
 New Google Leak mendedahkan perubahan langganan untuk Gemini AIApr 27, 2025 am 11:08 AM
New Google Leak mendedahkan perubahan langganan untuk Gemini AIApr 27, 2025 am 11:08 AMGemini Google Advanced: Tahap Langganan Baru di Horizon Pada masa ini, mengakses Gemini Advanced memerlukan pelan premium AI $ 19.99/bulan. Walau bagaimanapun, laporan Pihak Berkuasa Android menunjukkan perubahan yang akan datang. Kod dalam google terkini p
 Bagaimana Pecutan Analisis Data Menyelesaikan Bots Tersembunyi AIApr 27, 2025 am 11:07 AM
Bagaimana Pecutan Analisis Data Menyelesaikan Bots Tersembunyi AIApr 27, 2025 am 11:07 AMWalaupun gembar -gembur di sekitar keupayaan AI maju, satu cabaran penting bersembunyi dalam perusahaan AI perusahaan: kesesakan pemprosesan data. Walaupun CEO merayakan kemajuan AI, jurutera bergelut dengan masa pertanyaan yang perlahan, saluran paip yang terlalu banyak, a
 Markitdown MCP boleh menukar mana -mana dokumen ke Markdowns!Apr 27, 2025 am 09:47 AM
Markitdown MCP boleh menukar mana -mana dokumen ke Markdowns!Apr 27, 2025 am 09:47 AMDokumen pengendalian tidak lagi hanya mengenai pembukaan fail dalam projek AI anda, ia mengenai mengubah kekacauan menjadi kejelasan. Dokumen seperti PDF, PowerPoints, dan perkataan banjir aliran kerja kami dalam setiap bentuk dan saiz. Mengambil semula berstruktur
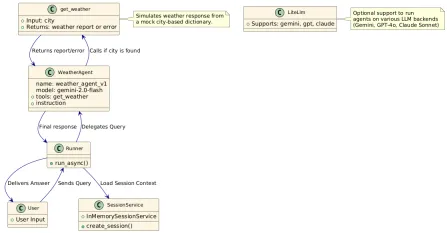 Bagaimana cara menggunakan Google ADK untuk ejen bangunan? - Analytics VidhyaApr 27, 2025 am 09:42 AM
Bagaimana cara menggunakan Google ADK untuk ejen bangunan? - Analytics VidhyaApr 27, 2025 am 09:42 AMMemanfaatkan kuasa Kit Pembangunan Ejen Google (ADK) untuk membuat ejen pintar dengan keupayaan dunia sebenar! Tutorial ini membimbing anda melalui membina ejen perbualan menggunakan ADK, menyokong pelbagai model bahasa seperti Gemini dan GPT. W
 Penggunaan SLM Over LLM untuk Penyelesaian Masalah Berkesan - Analisis VidhyaApr 27, 2025 am 09:27 AM
Penggunaan SLM Over LLM untuk Penyelesaian Masalah Berkesan - Analisis VidhyaApr 27, 2025 am 09:27 AMRingkasan: Model bahasa kecil (SLM) direka untuk kecekapan. Mereka lebih baik daripada model bahasa yang besar (LLM) dalam persekitaran yang kurang sensitif, masa nyata dan privasi. Terbaik untuk tugas-tugas berasaskan fokus, terutamanya di mana kekhususan domain, kawalan, dan tafsiran lebih penting daripada pengetahuan umum atau kreativiti. SLMs bukan pengganti LLM, tetapi mereka sesuai apabila ketepatan, kelajuan dan keberkesanan kos adalah kritikal. Teknologi membantu kita mencapai lebih banyak sumber. Ia sentiasa menjadi promoter, bukan pemandu. Dari era enjin stim ke era gelembung internet, kuasa teknologi terletak pada tahap yang membantu kita menyelesaikan masalah. Kecerdasan Buatan (AI) dan AI Generatif Baru -baru ini tidak terkecuali
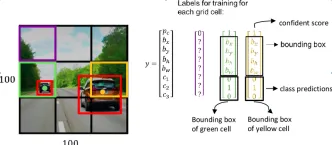 Bagaimana cara menggunakan model Google Gemini untuk tugas penglihatan komputer? - Analytics VidhyaApr 27, 2025 am 09:26 AM
Bagaimana cara menggunakan model Google Gemini untuk tugas penglihatan komputer? - Analytics VidhyaApr 27, 2025 am 09:26 AMMemanfaatkan kekuatan Google Gemini untuk Visi Komputer: Panduan Komprehensif Google Gemini, chatbot AI terkemuka, memanjangkan keupayaannya di luar perbualan untuk merangkumi fungsi penglihatan komputer yang kuat. Panduan ini memperincikan cara menggunakan
 Gemini 2.0 Flash vs O4-Mini: Bolehkah Google lebih baik daripada Openai?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini: Bolehkah Google lebih baik daripada Openai?Apr 27, 2025 am 09:20 AMLandskap AI pada tahun 2025 adalah elektrik dengan kedatangan Flash Gemini 2.0 Google dan Openai's O4-mini. Model-model canggih ini, yang dilancarkan minggu-minggu, mempunyai ciri-ciri canggih yang setanding dan skor penanda aras yang mengagumkan. Perbandingan mendalam ini


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

VSCode Windows 64-bit Muat Turun
Editor IDE percuma dan berkuasa yang dilancarkan oleh Microsoft

SublimeText3 Linux versi baharu
SublimeText3 Linux versi terkini

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

mPDF
mPDF ialah perpustakaan PHP yang boleh menjana fail PDF daripada HTML yang dikodkan UTF-8. Pengarang asal, Ian Back, menulis mPDF untuk mengeluarkan fail PDF "dengan cepat" dari tapak webnya dan mengendalikan bahasa yang berbeza. Ia lebih perlahan dan menghasilkan fail yang lebih besar apabila menggunakan fon Unicode daripada skrip asal seperti HTML2FPDF, tetapi menyokong gaya CSS dsb. dan mempunyai banyak peningkatan. Menyokong hampir semua bahasa, termasuk RTL (Arab dan Ibrani) dan CJK (Cina, Jepun dan Korea). Menyokong elemen peringkat blok bersarang (seperti P, DIV),






