Penjelasan ringkas tentang fungsi ketumpatan kebarangkalian

Bolehkah anda terangkan secara ringkas apakah fungsi ketumpatan kebarangkalian?

Fungsi ketumpatan kebarangkalian (p.d.f., fungsi ketumpatan kebarangkalian) menerangkan taburan kebarangkalian pembolehubah rawak dan merupakan fungsi terbitan bagi fungsi taburan kumulatif. [Sunting] Definisi: Untuk pembolehubah rawak nyata satu dimensi $int\_\{-infty\}^\{infty\}\; f\_\; (x),dx\; =\; 1$ Kebarangkalian pembolehubah rawak X dalam selang boleh dinyatakan dengan kamiran pasti baginya fungsi ketumpatan kebarangkalian: $P[a\; Dan$ F(x)=P[Xialah\; fungsi\; taburan\; kumulatif\; X.\; Jelas\; sekali\; fungsi\; ketumpatan\; kebarangkalian\; ialah\; fungsi\; terbitannya.\; [Sunting]Momen\; Aplikasi\; seperti\; nilai\; yang\; dijangkakan\; dan\; variasi\; boleh\; diperolehi\; daripada\; fungsi\; ketumpatan\; kebarangkalian.\; Nilai\; dijangka\; (saat\; pertama):\; E[X]=$ int\_\{-infty\}^\{infty\}\; xf(x),dx\; Variasi\; (saat\; kedua):\; VAR[X]=$ int\_\{-infty\}^\{\; infty\}\; (x-E[X])^2f(x),dx[sunting]\; Fungsi\; ciri\; boleh\; didapati\; dengan\; Fourier\; mengubah\; fungsi\; ketumpatan\; kebarangkalian.$ Phi\_X(jomega)\; =\; int\_\{-infty\}^\{infty\}\; f(x)e^\{jomega\; x\},dx$Terdapat\; hubungan\; satu\; dengan\; satu\; antara\; fungsi\; ciri\; dan\; fungsi\; ketumpatan\; kebarangkalian.\; Oleh\; itu,\; mengetahui\; fungsi\; ciri\; taburan\; adalah\; bersamaan\; dengan\; mengetahui\; fungsi\; ketumpatan\; kebarangkalian\; taburan.\; da:Sandsynlighedst\ae thedsfunktion\; en:Ketumpatan\; kebarangkalian\; berfungsi:Funzione\; di\; densità\; di\; probabilità\; nl:Kansdichtheid\; sv:Täthetsfunktion$ $Rasuk\; zarah\; disebarkan\; oleh\; halangan\; (terletak\; pada\; x\; =\; 0\; fungsi\; gelombangnya\; adalah\; seperti\; berikut:$ ).$\Psi (x,\; t)\; =\; Ae-iEt/j[apabila\; x$$$$

Ψ（x, t） = e-iEt/h( Beikx+ Ce-ikx) [apabila x> 0 ]

Di mana E = h2k2/( 2m ) dan k > 0, A, B dan C ialah pekali kompleks.

﹝"h" ialah "h-bar", iaitu garis mendatar di atas h﹞

(a) Kira ketumpatan kebarangkaliannya p(x, t) apabila x

(b) Kira ketumpatan aliran kebarangkaliannya j(x, t) apabila x

(c) Kira ketumpatan kebarangkaliannya p(x, t) apabila x > 0.

(d) Kira ketumpatan aliran kebarangkaliannya j(x, t) apabila x > 0.

(e) Fungsi gelombang di atas mengandungi tiga bahagian berbeza, tiga pekali A, B dan C. Beritahu sama ada setiap satu bergerak ke kanan atau kiri. Ketiga-tiga mereka mewakili kejadian, pantulan dan pelepasan yang mana satu?

Nota: Jawapan kepada p(x, t) dan j(x,t) mestilah nombor nyata.

Bagaimana untuk membezakan antara fungsi kebarangkalian dan ketumpatan kebarangkalian

Takrifan matematik ketumpatan kebarangkalian

Untuk pembolehubah rawak X, jika terdapat fungsi boleh integrasi bukan negatif p(x) (﹣∞

Pembolehubah rawak berterusan sering digambarkan secara intuitif oleh fungsi ketumpatan kebarangkalian Fungsi ketumpatan kebarangkalian f(x) pembolehubah rawak selanjar mempunyai sifat berikut:

Ini merujuk kepada pembolehubah rawak berterusan satu dimensi, dan pembolehubah selanjar berbilang dimensi adalah serupa.

Fungsi ketumpatan kebarangkalian data rawak: mewakili kebarangkalian bahawa amplitud serta-merta berada dalam julat yang ditentukan, dan oleh itu merupakan fungsi amplitud. Ia berbeza dengan magnitud julat yang diambil.

Fungsi ketumpatan f(x) mempunyai sifat berikut:

(1)f(x)≧0;

(2) ∫f(x)d(x)=1;

(3) P(a

Andaikan fungsi ketumpatan kebarangkalian pembolehubah rawak X N0 1 Y |x| Y

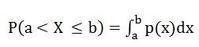Proses penyelesaian masalah adalah seperti berikut:

Maklumat lanjutan

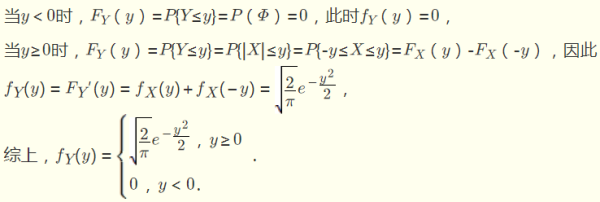Kaedah ketumpatan kebarangkalian:

Katakan pembolehubah rawak Antaranya, α=min(g(-∞), g(∞)), β=max(g(-∞), g(∞)), h(y) ialah fungsi songsang bagi g(x).

Sekadar bercakap tentang ketumpatan kebarangkalian tidak mempunyai kepentingan praktikal Ia mesti mempunyai selang sempadan tertentu sebagai premis. Ketumpatan kebarangkalian boleh dianggap sebagai ordinat dan selang sebagai absis. Kamiran ketumpatan kebarangkalian di atas selang ialah luas, dan kawasan ini ialah kebarangkalian kejadian yang berlaku dalam selang ini . Oleh itu, adalah tidak bermakna untuk menganalisis ketumpatan kebarangkalian titik sahaja. Ia mesti mempunyai selang sebagai rujukan dan perbandingan.

Kebarangkalian merujuk kepada kebarangkalian sesuatu peristiwa berlaku secara rawak Untuk fungsi taburan seragam, ketumpatan kebarangkalian adalah sama dengan kebarangkalian selang (julat nilai peristiwa) dibahagikan dengan panjang selang itu. negatif dan boleh menjadi sangat besar atau sangat kecil. Pilih satu produk secara rawak daripada kumpulan produk tulen dan rosak, dan "yang anda lukis adalah tulen" ialah acara rawak. Katakan satu fenomena rawak diuji dan diperhatikan n kali, dan peristiwa A berlaku m kali, iaitu kekerapan kejadiannya ialah m/n. Selepas banyak percubaan berulang, m/n selalunya menjadi lebih dekat dan lebih dekat kepada pemalar tertentu (lihat hukum Bernoulli nombor besar untuk bukti kesimpulan ini).

Atas ialah kandungan terperinci Penjelasan ringkas tentang fungsi ketumpatan kebarangkalian. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!