 Peranti teknologi
Peranti teknologi AI
AI Menggunakan algoritma genetik rangkaian saraf untuk menyelesaikan masalah nilai ekstrem fungsi
Menggunakan algoritma genetik rangkaian saraf untuk menyelesaikan masalah nilai ekstrem fungsiMenggunakan algoritma genetik rangkaian saraf untuk menyelesaikan masalah nilai ekstrem fungsi

Fungsi algoritma genetik rangkaian saraf pengoptimuman nilai melampau ialah algoritma pengoptimuman yang menggunakan algoritma genetik dan rangkaian saraf secara menyeluruh. Idea terasnya ialah menggunakan model rangkaian saraf untuk menganggarkan fungsi objektif dan mencari penyelesaian optimum melalui algoritma genetik. Berbanding dengan algoritma pengoptimuman lain, algoritma genetik rangkaian saraf mempunyai keupayaan dan keteguhan carian global yang lebih kukuh, dan boleh menyelesaikan masalah nilai ekstrem fungsi tak linear yang kompleks dengan cekap. Kelebihan algoritma ini ialah ia boleh menganggarkan fungsi objektif yang kompleks melalui keupayaan pembelajaran rangkaian saraf, dan secara global mencari penyelesaian optimum melalui strategi carian algoritma genetik. Dengan menggunakan sepenuhnya kelebihan rangkaian saraf dan algoritma genetik, fungsi algoritma genetik rangkaian saraf pengoptimuman nilai melampau mempunyai potensi yang luas dalam aplikasi praktikal.
Untuk fungsi tak linear yang tidak diketahui, sukar untuk mencari nilai ekstrem fungsi dengan tepat hanya melalui data input dan output fungsi tersebut. Untuk menyelesaikan masalah seperti ini, kaedah rangkaian saraf yang digabungkan dengan algoritma genetik boleh digunakan. Rangkaian saraf mempunyai keupayaan pemasangan tak linear dan boleh muat fungsi algoritma genetik mempunyai keupayaan pengoptimuman tak linear dan boleh mencari titik ekstrem fungsi. Dengan menggabungkan kedua-dua kaedah ini, nilai ekstrem fungsi boleh didapati dengan lebih tepat.
Pengoptimuman nilai ekstrem fungsi algoritma genetik rangkaian saraf terutamanya dibahagikan kepada dua langkah: Latihan rangkaian saraf BP dan pemasangan dan pengoptimuman nilai ekstrem algoritma genetik.
Pertama, gunakan rangkaian neural BP untuk melatih dan menyesuaikan data input Melalui proses pembelajaran, rangkaian saraf boleh menghampiri fungsi objektif dan dengan itu meramalkan hasil output. Matlamat teras langkah ini adalah untuk melatih rangkaian saraf supaya ia dapat menyesuaikan data input dengan tepat dan mengubah masalah menjadi masalah mencari penyelesaian yang optimum.
Kemudian, algoritma genetik digunakan untuk melaraskan pemberat rangkaian saraf, menggunakan operasi seperti pemilihan, silang dan mutasi untuk mencari penyelesaian terbaik. Tujuan utama langkah ini adalah untuk menggunakan ciri carian global dan keteguhan algoritma genetik untuk mencari kombinasi optimum berat rangkaian saraf, supaya output ramalan rangkaian saraf mencapai tahap terbaik.
Melalui dua langkah di atas, algoritma genetik rangkaian saraf berfungsi pengoptimuman nilai melampau boleh mengubah masalah nilai ekstrem fungsi tak linear kepada masalah mencari penyelesaian optimum, dan menggunakan kelebihan rangkaian saraf dan algoritma genetik untuk mencari yang optimum penyelesaian .
Perlu diingatkan bahawa fungsi algoritma genetik rangkaian saraf pengoptimuman nilai ekstrem perlu disesuaikan dan dioptimumkan untuk masalah tertentu, termasuk pemilihan parameter seperti struktur rangkaian saraf, bilangan lapisan, bilangan nod, fungsi pengaktifan, dan algoritma genetik, dsb. Pada masa yang sama, untuk masalah yang kompleks, parameter dan struktur algoritma mungkin perlu dilaraskan untuk mendapatkan hasil pengoptimuman yang lebih baik.
Contoh Pengoptimuman Nilai Ekstrim Fungsi Algoritma Genetik Rangkaian Neural
Andaikan kita mempunyai fungsi tak linear f(x,y)=x^2+y^2, dan kami berharap dapat mencari titik nilai minimum bagi fungsi ini .
Pertama, kita boleh menggunakan rangkaian neural untuk menyesuaikan fungsi ini. Kami memilih struktur rangkaian saraf yang mudah, seperti lapisan input (2 nod, sepadan dengan x dan y), lapisan tersembunyi (5 nod), dan lapisan output (1 nod, sepadan dengan nilai output fungsi) . Kami menggunakan 4000 set data latihan dan melatih serta muat melalui rangkaian saraf BP untuk membolehkan rangkaian saraf mempelajari peraturan fungsi f(x,y).
Kemudian, kami menggunakan algoritma genetik untuk mengoptimumkan rangkaian saraf terlatih. Kami menganggap berat rangkaian saraf sebagai individu, dan setiap individu mempunyai nilai kecergasan ini ialah nilai keluaran yang diramalkan oleh rangkaian saraf. Kami terus mengoptimumkan individu melalui operasi seperti pemilihan, persilangan dan mutasi sehingga kami menemui individu yang optimum, iaitu gabungan pemberat rangkaian saraf yang optimum.
Melalui fungsi algoritma genetik rangkaian saraf pengoptimuman nilai melampau, kita boleh mencari titik nilai minimum bagi fungsi f(x,y). Nilai input yang sepadan dengan titik minimum ini ialah nilai input yang sepadan dengan gabungan optimum berat rangkaian saraf. Proses pelaksanaan yang sepadan adalah seperti berikut:
import numpy as np
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from scipy.optimize import minimize
# 定义目标函数
def f(x):
return x[0]**2 + x[1]**2
# 生成训练数据和测试数据
X = np.random.rand(4000, 2)
y = f(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练神经网络
mlp = MLPRegressor(hidden_layer_sizes=(5,), activation='relu', solver='adam', max_iter=1000)
mlp.fit(X_train, y_train)
# 定义遗传算法优化函数
def nnga_optimize(x0):
# 定义适应度函数
def fitness(x):
return -f(x) # 适应度函数取负值,因为我们要找极小值点
# 定义遗传算法参数
args = (mlp.coefs_, mlp.intercepts_)
options = {'maxiter': 1000}
# 定义约束条件,限制搜索范围在一个小区域内
bounds = [(0, 1), (0, 1)]
# 使用scipy的minimize函数进行优化
res = minimize(fitness, x0, args=args, bounds=bounds, method='SLSQP', options=options)
return res.x
# 进行遗传算法优化,找到最优解
x_opt = nnga_optimize([0.5, 0.5])
print('最优解:', x_opt)Atas ialah kandungan terperinci Menggunakan algoritma genetik rangkaian saraf untuk menyelesaikan masalah nilai ekstrem fungsi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Apakah graf pemikiran dalam kejuruteraan segeraApr 13, 2025 am 11:53 AM
Apakah graf pemikiran dalam kejuruteraan segeraApr 13, 2025 am 11:53 AMPengenalan Dalam kejuruteraan segera, "Grafik Pemikiran" merujuk kepada pendekatan baru yang menggunakan teori graf untuk struktur dan membimbing proses penalaran AI. Tidak seperti kaedah tradisional, yang sering melibatkan linear
 Mengoptimumkan pemasaran e -mel organisasi anda dengan agen genaiApr 13, 2025 am 11:44 AM
Mengoptimumkan pemasaran e -mel organisasi anda dengan agen genaiApr 13, 2025 am 11:44 AMPengenalan Tahniah! Anda menjalankan perniagaan yang berjaya. Melalui laman web anda, kempen media sosial, webinar, persidangan, sumber percuma, dan sumber lain, anda mengumpul 5000 ID e -mel setiap hari. Langkah jelas seterusnya adalah
 Pemantauan Prestasi Aplikasi Masa Nyata dengan Apache PinotApr 13, 2025 am 11:40 AM
Pemantauan Prestasi Aplikasi Masa Nyata dengan Apache PinotApr 13, 2025 am 11:40 AMPengenalan Dalam persekitaran pembangunan perisian pantas hari ini, memastikan prestasi aplikasi yang optimum adalah penting. Memantau metrik masa nyata seperti masa tindak balas, kadar ralat, dan penggunaan sumber dapat membantu utama
 Chatgpt mencecah 1 bilion pengguna? 'Dua kali ganda dalam beberapa minggu' kata Ketua Pegawai Eksekutif OpenaiApr 13, 2025 am 11:23 AM
Chatgpt mencecah 1 bilion pengguna? 'Dua kali ganda dalam beberapa minggu' kata Ketua Pegawai Eksekutif OpenaiApr 13, 2025 am 11:23 AM"Berapa banyak pengguna yang anda ada?" Dia ditakdirkan. "Saya fikir kali terakhir yang kami katakan ialah 500 juta aktif mingguan, dan ia berkembang dengan pesat," jawab Altman. "Anda memberitahu saya bahawa ia seperti dua kali ganda dalam beberapa minggu sahaja," kata Anderson. "Saya mengatakan bahawa priv
 Pixtral -12b: Model Multimodal Pertama Mistral Ai 'Apr 13, 2025 am 11:20 AM
Pixtral -12b: Model Multimodal Pertama Mistral Ai 'Apr 13, 2025 am 11:20 AMPengenalan Mistral telah mengeluarkan model multimodal yang pertama, iaitu Pixtral-12B-2409. Model ini dibina atas parameter 12 bilion Mistral, NEMO 12B. Apa yang membezakan model ini? Ia kini boleh mengambil kedua -dua gambar dan Tex
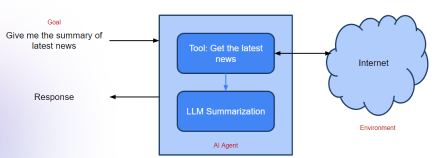 Rangka Kerja Agentik untuk Aplikasi AI Generatif - Analytics VidhyaApr 13, 2025 am 11:13 AM
Rangka Kerja Agentik untuk Aplikasi AI Generatif - Analytics VidhyaApr 13, 2025 am 11:13 AMBayangkan mempunyai pembantu berkuasa AI yang bukan sahaja memberi respons kepada pertanyaan anda tetapi juga mengumpulkan maklumat, melaksanakan tugas, dan juga mengendalikan pelbagai jenis teks, imej, dan kod. Bunyi futuristik? Dalam ini a
 Aplikasi AI Generatif di Sektor KewanganApr 13, 2025 am 11:12 AM
Aplikasi AI Generatif di Sektor KewanganApr 13, 2025 am 11:12 AMPengenalan Industri kewangan adalah asas kepada mana -mana pembangunan negara, kerana ia memacu pertumbuhan ekonomi dengan memudahkan urus niaga yang cekap dan ketersediaan kredit. The ease with which transactions occur and credit
 Panduan untuk pembelajaran dalam talian dan algoritma pasif-agresifApr 13, 2025 am 11:09 AM
Panduan untuk pembelajaran dalam talian dan algoritma pasif-agresifApr 13, 2025 am 11:09 AMPengenalan Data dijana pada kadar yang belum pernah terjadi sebelumnya dari sumber seperti media sosial, urus niaga kewangan, dan platform e-dagang. Mengendalikan aliran maklumat yang berterusan ini adalah satu cabaran, tetapi ia menawarkan


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Penyesuai Pelayan SAP NetWeaver untuk Eclipse
Integrasikan Eclipse dengan pelayan aplikasi SAP NetWeaver.

Muat turun versi mac editor Atom
Editor sumber terbuka yang paling popular

ZendStudio 13.5.1 Mac
Persekitaran pembangunan bersepadu PHP yang berkuasa

VSCode Windows 64-bit Muat Turun
Editor IDE percuma dan berkuasa yang dilancarkan oleh Microsoft

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa





