
Dalam pembelajaran mesin, operasi matriks ialah alat matematik penting yang digunakan untuk memproses dan mengubah data. Dengan mewakili data dalam bentuk matriks, anda boleh melakukan pelbagai operasi algebra linear seperti pendaraban matriks, penambahan dan operasi songsang. Operasi ini boleh digunakan untuk transformasi ciri, pengoptimuman parameter dan pengiraan ramalan semasa latihan model dan inferens. Melalui operasi matriks, kami boleh memproses set data berskala besar dengan berkesan dan memanfaatkan pengkomputeran selari untuk mempercepatkan proses pengiraan. Selain itu, operasi matriks berkait rapat dengan bidang seperti pengekstrakan ciri, pengurangan dimensi dan pemprosesan imej, menyediakan asas matematik dan alatan yang berkuasa untuk pembelajaran mesin.
Operasi matriks digunakan secara meluas dalam pembelajaran mesin Beberapa senario aplikasi biasa akan diperkenalkan secara terperinci di bawah.
1. Regresi Linear
Regression linear ialah algoritma pembelajaran mesin yang digunakan untuk mewujudkan hubungan linear antara pembolehubah. Ia sesuai dengan perbezaan antara titik data dan model linear dengan meminimumkan fungsi objektif. Lazimnya, fungsi objektif menggunakan ralat min kuasa dua untuk mengukur tahap kesesuaian. Untuk menyelesaikan pekali regresi dan membuat ramalan, operasi matriks boleh dilakukan menggunakan kaedah seperti persamaan normal atau keturunan kecerunan.
2. Analisis Komponen Utama (PCA)
Analisis Komponen Utama ialah teknik pengurangan dimensi yang biasa digunakan untuk mengekstrak ciri yang paling penting daripada set data berdimensi tinggi. PCA memetakan data asal ke ruang ciri baharu supaya korelasi antara ciri baharu adalah minimum. Proses pemetaan ini melibatkan penguraian nilai eigen bagi matriks kovarians data dan memilih vektor eigen yang sepadan dengan nilai eigen terbesar sebagai komponen utama. Melalui operasi matriks, algoritma PCA boleh dilaksanakan dengan berkesan.
3. Rangkaian Neural
Rangkaian saraf ialah model pembelajaran mesin yang menyerupai cara kerja neuron dalam otak manusia. Rangkaian saraf biasanya terdiri daripada beberapa lapisan neuron, dengan setiap neuron disambungkan kepada semua neuron dalam lapisan seterusnya. Dalam rangkaian saraf, input dan pemberat diwakili sebagai matriks, dan maklumat dipindahkan dan diubah melalui gabungan pendaraban matriks dan fungsi pengaktifan tak linear. Operasi matriks memainkan peranan penting dalam rangkaian saraf, digunakan untuk mengira input dan output setiap neuron, serta mengemas kini parameter rangkaian (berat dan berat sebelah).
4. Pemprosesan imej
Pemprosesan imej ialah satu lagi bidang aplikasi penting dalam pembelajaran mesin. Imej biasanya diwakili sebagai matriks nilai piksel. Dengan melaksanakan operasi matriks pada matriks imej, pelbagai tugas pemprosesan imej boleh dicapai, seperti penapisan imej, pengesanan tepi, peningkatan imej, dsb. Teknik pemprosesan imej biasa, seperti rangkaian saraf konvolusi, menggunakan operasi konvolusi untuk mengekstrak dan mengklasifikasikan imej.
5. Sistem pengesyoran
Sistem pengesyoran ialah teknologi utama yang membantu pengguna menemui minat yang diperibadikan. Sistem pengesyoran berdasarkan operasi matriks sering digunakan untuk menganalisis interaksi antara pengguna dan item dan meramal item yang pengguna mungkin berminat. Dengan mewakili penilaian pengguna atau rekod tingkah laku sebagai matriks, kaedah seperti pemfaktoran matriks boleh digunakan untuk membuat kesimpulan ciri tersembunyi antara pengguna dan item untuk memberikan pengesyoran yang diperibadikan.
Ringkasnya, operasi matriks dalam pembelajaran mesin memainkan peranan penting dalam berbilang senario aplikasi. Mereka boleh memproses data berdimensi tinggi dengan berkesan, mengekstrak ciri, mengoptimumkan parameter model dan melaksanakan tugas transformasi dan ramalan data yang kompleks. Dengan menggunakan operasi matriks, kami boleh memahami dan menggunakan data dengan lebih baik serta membina model pembelajaran mesin yang lebih tepat dan berkesan.
Atas ialah kandungan terperinci Pengiraan matriks dan amalan dalam pembelajaran mesin. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
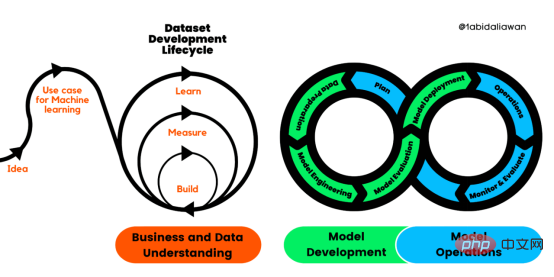 解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM
解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM译者 | 布加迪审校 | 孙淑娟目前,没有用于构建和管理机器学习(ML)应用程序的标准实践。机器学习项目组织得不好,缺乏可重复性,而且从长远来看容易彻底失败。因此,我们需要一套流程来帮助自己在整个机器学习生命周期中保持质量、可持续性、稳健性和成本管理。图1. 机器学习开发生命周期流程使用质量保证方法开发机器学习应用程序的跨行业标准流程(CRISP-ML(Q))是CRISP-DM的升级版,以确保机器学习产品的质量。CRISP-ML(Q)有六个单独的阶段:1. 业务和数据理解2. 数据准备3. 模型
 2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM
2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM机器学习是一个不断发展的学科,一直在创造新的想法和技术。本文罗列了2023年机器学习的十大概念和技术。 本文罗列了2023年机器学习的十大概念和技术。2023年机器学习的十大概念和技术是一个教计算机从数据中学习的过程,无需明确的编程。机器学习是一个不断发展的学科,一直在创造新的想法和技术。为了保持领先,数据科学家应该关注其中一些网站,以跟上最新的发展。这将有助于了解机器学习中的技术如何在实践中使用,并为自己的业务或工作领域中的可能应用提供想法。2023年机器学习的十大概念和技术:1. 深度神经网
 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
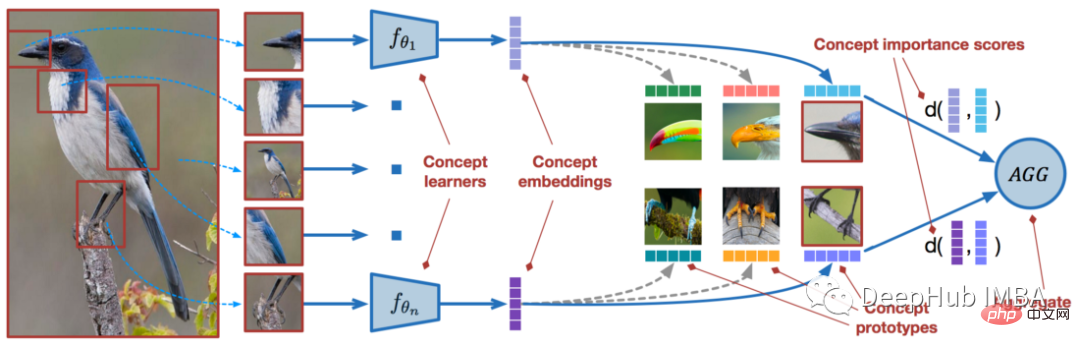 使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM
使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM近年来,基于深度学习的模型在目标检测和图像识别等任务中表现出色。像ImageNet这样具有挑战性的图像分类数据集,包含1000种不同的对象分类,现在一些模型已经超过了人类水平上。但是这些模型依赖于监督训练流程,标记训练数据的可用性对它们有重大影响,并且模型能够检测到的类别也仅限于它们接受训练的类。由于在训练过程中没有足够的标记图像用于所有类,这些模型在现实环境中可能不太有用。并且我们希望的模型能够识别它在训练期间没有见到过的类,因为几乎不可能在所有潜在对象的图像上进行训练。我们将从几个样本中学习
 LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM
LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。 摘要本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。本文包括的内容如下:简介LazyPredict模块的安装在分类模型中实施LazyPredict
 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
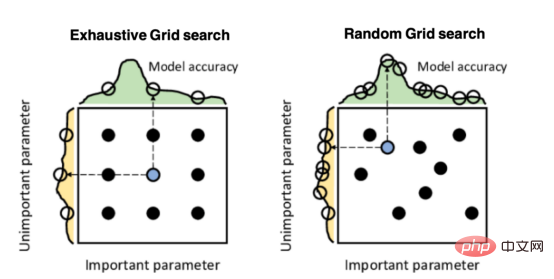
 超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM
超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM本文将详细介绍用来提高机器学习效果的最常见的超参数优化方法。 译者 | 朱先忠审校 | 孙淑娟简介通常,在尝试改进机器学习模型时,人们首先想到的解决方案是添加更多的训练数据。额外的数据通常是有帮助(在某些情况下除外)的,但生成高质量的数据可能非常昂贵。通过使用现有数据获得最佳模型性能,超参数优化可以节省我们的时间和资源。顾名思义,超参数优化是为机器学习模型确定最佳超参数组合以满足优化函数(即,给定研究中的数据集,最大化模型的性能)的过程。换句话说,每个模型都会提供多个有关选项的调整“按钮
 人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM
人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM实现自我完善的过程是“机器学习”。机器学习是人工智能核心,是使计算机具有智能的根本途径;它使计算机能模拟人的学习行为,自动地通过学习来获取知识和技能,不断改善性能,实现自我完善。机器学习主要研究三方面问题:1、学习机理,人类获取知识、技能和抽象概念的天赋能力;2、学习方法,对生物学习机理进行简化的基础上,用计算的方法进行再现;3、学习系统,能够在一定程度上实现机器学习的系统。


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Versi Mac WebStorm
Alat pembangunan JavaScript yang berguna

Dreamweaver Mac版
Alat pembangunan web visual

Pelayar Peperiksaan Selamat
Pelayar Peperiksaan Selamat ialah persekitaran pelayar selamat untuk mengambil peperiksaan dalam talian dengan selamat. Perisian ini menukar mana-mana komputer menjadi stesen kerja yang selamat. Ia mengawal akses kepada mana-mana utiliti dan menghalang pelajar daripada menggunakan sumber yang tidak dibenarkan.

VSCode Windows 64-bit Muat Turun
Editor IDE percuma dan berkuasa yang dilancarkan oleh Microsoft

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma





