Apakah prinsip interaksi antara tensor multidimensi dan lapisan linear?

Lapisan linear ialah salah satu lapisan yang paling biasa digunakan dalam pembelajaran mendalam dan memainkan peranan penting dalam rangkaian saraf. Ia digunakan secara meluas dalam tugas seperti klasifikasi imej, pengesanan objek dan pengecaman pertuturan. Artikel ini akan menumpukan pada peranan lapisan linear pada tensor berbilang dimensi.
Pertama, mari kita semak prinsip asas lapisan linear. Untuk tensor input x, formula pengiraan lapisan linear adalah seperti berikut:
y=Wx+b
di mana, W dan b ialah parameter bagi lapisan linear masing-masing, dan bentuk W ialah (n_out, n_in), b Bentuknya ialah (n_out,). n_in mewakili saiz tensor input, dan n_out mewakili saiz tensor output. Andaikan bahawa tensor input ialah tensor satu dimensi x∈R^n_in, dan tensor output juga ialah tensor satu dimensi y∈R^n_out. Dalam lapisan linear, tensor input diubah secara linear oleh matriks berat W, ditambah vektor pincang b, untuk mendapatkan tensor keluaran y. Penjelmaan linear ini boleh dinyatakan sebagai y = Wx + b. Antaranya, setiap baris W mewakili vektor berat neuron keluaran lapisan linear, dan setiap elemen b mewakili nilai pincang neuron keluaran yang sepadan. Setiap elemen tensor keluaran akhir y diperoleh dengan melakukan hasil darab titik antara vektor berat neuron keluaran yang sepadan dan tensor input, ditambah dengan nilai offset yang sepadan.
Sekarang, katakan kita mempunyai tensor berbilang dimensi X dengan bentuk (n_1,n_2,…,n_k). Kita perlu menghantarnya ke lapisan linear untuk menghasilkan tensor keluaran Y dengan bentuk (m_1,m_2,…,m_l). Pada masa ini, apa yang perlu kita lakukan?
Pertama, kita perlu meratakan X menjadi tensor satu dimensi. Proses ini sering dipanggil operasi "meratakan" dan boleh dilaksanakan menggunakan fungsi pandangan dalam PyTorch. Secara khusus, kita boleh menukar bentuk X kepada (n_1kali n_2kali...kali n_k,), iaitu, susun elemen semua dimensi dalam satu lajur. Dengan cara ini, kita mendapat tensor satu dimensi x, yang saiznya ialah n_{in}=n_1kali n_2kali...kali n_k.
Seterusnya, kita boleh melepasi x ke lapisan linear dan mendapatkan tensor keluaran y. Secara khusus, kita boleh menggunakan formula pengiraan lapisan linear:
y=Wx+b
Di sini, bentuk W ialah (m_{keluar},n_{in}), dan bentuk b ialah (m_{ out},), m_{out} mewakili saiz tensor keluaran. Hasil pendaraban Wx ialah tensor satu dimensi dengan bentuk (m_{out},).
Akhir sekali, kita perlu menukar y kembali kepada bentuk tensor berbilang dimensi. Secara khusus, kita boleh menggunakan fungsi pandangan dalam PyTorch untuk menukar bentuk y kepada (m_1, m_2,...,m_l). Dengan cara ini, kita mendapat tensor keluaran akhir Y.
Perlu diingatkan bahawa apabila meratakan tensor berbilang dimensi menjadi tensor satu dimensi, kita perlu memastikan bahawa susunan elemen dalam tensor kekal tidak berubah. Sebagai contoh, katakan kita mempunyai tensor dua dimensi X bentuk (2,3):
Jika kita menggunakan view(-1) untuk melaksanakan, hasilnya ialah:
x=[1,2,3,4,5,6]
Di sini, kita akan (1,2) dan ( 4,5) Unsur-unsur dalam dua baris ini disusun bersama, menyebabkan susunannya berubah. Oleh itu, operasi yang betul hendaklah menggunakan view(-1) untuk meratakan tensor, dan kemudian gunakan view(1,-1) untuk menukarnya kembali kepada bentuk asalnya:
x=begin{bmatrix}1&2&3&4&5&6end{ bmatrix } Perlu diingatkan bahawa peranan lapisan linear pada tensor pelbagai dimensi boleh dilihat sebagai transformasi linear bebas untuk setiap sampel. Sebagai contoh, katakan kita mempunyai tensor empat dimensi X dengan bentuk (N, C, H, W), di mana N mewakili bilangan sampel, C mewakili bilangan saluran, dan H dan W mewakili ketinggian dan lebar masing-masing. Kita boleh kembangkan Lapisan linear melakukan transformasi linear bebas pada setiap sampel untuk mendapatkan tensor keluaran Y dengan bentuk (N, m_{out}). Akhir sekali, kita boleh memulihkan Y kepada bentuk asalnya (N,m_1,m_2,…,m_l) di sepanjang dimensi pertama. Ringkasnya, peranan lapisan linear pada tensor pelbagai dimensi boleh dilihat sebagai transformasi linear bebas untuk setiap sampel. Dalam aplikasi praktikal, kami biasanya meratakan tensor berbilang dimensi menjadi tensor satu dimensi dan menghantarnya ke lapisan linear. Operasi merata perlu memastikan susunan elemen kekal tidak berubah, jika tidak, ia akan membawa kepada hasil pengiraan yang salah. Akhir sekali, kita perlu memulihkan tensor keluaran kepada bentuk asalnya untuk langkah pengiraan seterusnya.Atas ialah kandungan terperinci Apakah prinsip interaksi antara tensor multidimensi dan lapisan linear?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
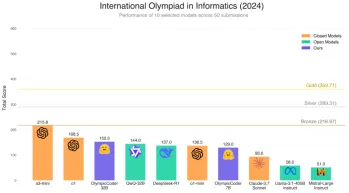 Adakah Model Model ' S 7B Olympiccoder mengalahkan Claude 3.7?Apr 23, 2025 am 11:49 AM
Adakah Model Model ' S 7B Olympiccoder mengalahkan Claude 3.7?Apr 23, 2025 am 11:49 AMMemeluk Olimpikcoder-7B: Model Penaakulan Kod Terbuka Sumber Terbuka yang kuat Perlumbaan untuk membangunkan model bahasa yang tertumpu kepada kod unggul semakin meningkat, dan Hugging Face telah menyertai pertandingan dengan pesaing yang hebat: Olympiccoder-7b, produk
 4 ciri Gemini baru yang anda tidak dapat merinduiApr 23, 2025 am 11:48 AM
4 ciri Gemini baru yang anda tidak dapat merinduiApr 23, 2025 am 11:48 AMBerapa banyak daripada anda yang berharap AI dapat melakukan lebih daripada sekadar menjawab soalan? Saya tahu saya ada, dan sejak kebelakangan ini, saya kagum dengan bagaimana ia berubah. AI Chatbots bukan sekadar berbual lagi, mereka sedang membuat, Researchin
 Camunda menulis skor baru untuk orkestra ai agentikApr 23, 2025 am 11:46 AM
Camunda menulis skor baru untuk orkestra ai agentikApr 23, 2025 am 11:46 AMOleh kerana Smart AI mula diintegrasikan ke dalam semua peringkat platform dan aplikasi perisian perusahaan (kita harus menekankan bahawa terdapat kedua -dua alat teras yang kuat dan beberapa alat simulasi yang kurang dipercayai), kita memerlukan satu set baru keupayaan infrastruktur untuk menguruskan agen -agen ini. Camunda, sebuah syarikat orkestrasi proses yang berpusat di Berlin, Jerman, percaya ia dapat membantu Smart AI memainkan peranannya yang sewajarnya dan selaras dengan matlamat dan peraturan perniagaan yang tepat di tempat kerja digital yang baru. Syarikat ini kini menawarkan keupayaan orkestra pintar yang direka untuk membantu model organisasi, menggunakan dan mengurus ejen AI. Dari perspektif kejuruteraan perisian praktikal, apakah maksudnya? Integrasi proses kepastian dan bukan deterministik Syarikat itu mengatakan yang penting adalah untuk membolehkan pengguna (biasanya saintis data, perisian)
 Adakah nilai dalam pengalaman AI perusahaan yang dikendalikan?Apr 23, 2025 am 11:45 AM
Adakah nilai dalam pengalaman AI perusahaan yang dikendalikan?Apr 23, 2025 am 11:45 AMMenghadiri Google Cloud Seterusnya '25, saya berminat untuk melihat bagaimana Google akan membezakan tawaran AInya. Pengumuman baru -baru ini mengenai Agentspace (dibincangkan di sini) dan Suite Pengalaman Pelanggan (dibincangkan di sini) menjanjikan, menekankan perniagaan Valu
 Bagaimana untuk mencari model penyembuhan berbilang bahasa terbaik untuk kain anda?Apr 23, 2025 am 11:44 AM
Bagaimana untuk mencari model penyembuhan berbilang bahasa terbaik untuk kain anda?Apr 23, 2025 am 11:44 AMMemilih model penyembuhan berbilang bahasa yang optimum untuk sistem pengambilan semula (RAG) pengambilan anda Di dunia yang saling berkaitan hari ini, membina sistem AI berbilang bahasa yang berkesan adalah yang paling utama. Model penyembuhan berbilang bahasa yang teguh adalah penting untuk Re
 Musk: Robotaxis di Austin memerlukan campur tangan setiap 10,000 batuApr 23, 2025 am 11:42 AM
Musk: Robotaxis di Austin memerlukan campur tangan setiap 10,000 batuApr 23, 2025 am 11:42 AMPelancaran Austin Robotaxi Tesla: Melihat lebih dekat dengan tuntutan Musk Elon Musk baru-baru ini mengumumkan pelancaran Robotaxi yang akan datang di Tesla di Austin, Texas, pada mulanya mengerahkan armada kecil 10-20 kenderaan untuk alasan keselamatan, dengan rancangan untuk pengembangan pesat. H
 AI 'Apr 23, 2025 am 11:41 AM
AI 'Apr 23, 2025 am 11:41 AMCara kecerdasan buatan digunakan mungkin tidak dijangka. Pada mulanya, ramai di antara kita mungkin berfikir ia digunakan terutamanya untuk tugas kreatif dan teknikal, seperti menulis kod dan membuat kandungan. Walau bagaimanapun, satu tinjauan baru -baru ini yang dilaporkan oleh Harvard Business Review menunjukkan bahawa ini tidak berlaku. Kebanyakan pengguna mencari kecerdasan buatan bukan hanya untuk kerja, tetapi untuk sokongan, organisasi, dan juga persahabatan! Laporan itu mengatakan bahawa kes permohonan AI yang pertama adalah rawatan dan persahabatan. Ini menunjukkan bahawa ketersediaan 24/7 dan keupayaan untuk memberikan nasihat dan maklum balas yang jujur, jujur adalah nilai yang sangat baik. Sebaliknya, tugas pemasaran (seperti menulis blog, mewujudkan jawatan media sosial, atau salinan pengiklanan) yang lebih rendah pada senarai penggunaan popular. Mengapa ini? Mari kita lihat hasil penyelidikan dan bagaimana ia terus menjadi
 Syarikat berlumba ke arah pengangkatan ejen AIApr 23, 2025 am 11:40 AM
Syarikat berlumba ke arah pengangkatan ejen AIApr 23, 2025 am 11:40 AMKebangkitan agen AI mengubah landskap perniagaan. Berbanding dengan revolusi awan, kesan agen AI diramalkan secara eksponen lebih besar, menjanjikan untuk merevolusikan kerja pengetahuan. Keupayaan untuk mensimulasikan keputusan-maki manusia


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

MantisBT
Mantis ialah alat pengesan kecacatan berasaskan web yang mudah digunakan yang direka untuk membantu dalam pengesanan kecacatan produk. Ia memerlukan PHP, MySQL dan pelayan web. Lihat perkhidmatan demo dan pengehosan kami.

EditPlus versi Cina retak
Saiz kecil, penyerlahan sintaks, tidak menyokong fungsi gesaan kod

ZendStudio 13.5.1 Mac
Persekitaran pembangunan bersepadu PHP yang berkuasa

Pelayar Peperiksaan Selamat
Pelayar Peperiksaan Selamat ialah persekitaran pelayar selamat untuk mengambil peperiksaan dalam talian dengan selamat. Perisian ini menukar mana-mana komputer menjadi stesen kerja yang selamat. Ia mengawal akses kepada mana-mana utiliti dan menghalang pelajar daripada menggunakan sumber yang tidak dibenarkan.

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)





