 Peranti teknologi
Peranti teknologi AI
AI Rangkaian saraf dalam untuk penentukuran klasifikasi dan penentukuran regresi
Rangkaian saraf dalam untuk penentukuran klasifikasi dan penentukuran regresiRangkaian saraf dalam untuk penentukuran klasifikasi dan penentukuran regresi

Rangkaian saraf dalam ialah model pembelajaran mesin berkuasa yang boleh mempelajari ciri dan corak secara automatik. Walau bagaimanapun, dalam aplikasi praktikal, output rangkaian saraf selalunya perlu ditentukur untuk meningkatkan prestasi dan kebolehpercayaan. Penentukuran klasifikasi dan penentukuran regresi adalah teknik penentukuran yang biasa digunakan, dan ia mempunyai prinsip dan aplikasi yang berbeza. Artikel ini akan memperkenalkan secara terperinci prinsip kerja dan senario aplikasi kedua-dua teknologi ini.
1. Penentukuran pengelasan
Penentukuran pengelasan adalah untuk meningkatkan kebolehpercayaan dan ketepatan pengelas, yang dicapai dengan melaraskan output vektor pengedaran kebarangkalian oleh pengelas. Dalam masalah klasifikasi, rangkaian saraf mengeluarkan vektor yang mewakili kebarangkalian yang diramalkan bagi setiap kelas. Walau bagaimanapun, kebarangkalian ini tidak selalu tepat dan mungkin berat sebelah terlalu tinggi atau terlalu rendah. Matlamat penentukuran klasifikasi adalah untuk melaraskan kebarangkalian ini untuk menjadikannya lebih dekat kepada taburan kebarangkalian sebenar. Ini meningkatkan prestasi pengelas, menjadikannya lebih dipercayai dalam meramalkan kebarangkalian kelas yang berbeza.
Kaedah penentukuran klasifikasi yang biasa digunakan termasuk dua yang berikut:
1 Penskalaan suhu
Penskalaan suhu ialah teknologi penentukuran klasifikasi yang mudah dan berkesan berdasarkan rangkaian keluaran, dan prinsipnya adalah berskala. , dengan itu melaraskan keyakinan pengelas. Khususnya, penskalaan suhu menskalakan output lapisan terakhir rangkaian saraf dengan memperkenalkan parameter suhu T, menukarkan kebarangkalian ramalan asal p kepada kebarangkalian q yang ditentukur:
q_i=\frac{p_i^{\frac{1}{T}}}{\sum_{j=1}^K p_j^{\frac{1}{T}}}di mana, i mewakili kategori ke-i, K mewakili jumlah bilangan kategori. Apabila T=1, penskalaan suhu tidak akan mengubah kebarangkalian ramalan asal Apabila T>1, penskalaan suhu akan meningkatkan keyakinan pengelas, menjadikan kebarangkalian ramalan lebih tertumpu dan yakin apabila T
Kelebihan penskalaan suhu ialah ia mudah dilaksanakan, kos rendah, dan boleh ditentukur tanpa melatih semula model. Walau bagaimanapun, penskalaan suhu tidak dijamin untuk meningkatkan prestasi pengelas secara berkesan dalam semua kes kerana ia menganggap bahawa ralat semua kategori adalah bebas dan pada skala yang sama, yang tidak semestinya benar dalam aplikasi praktikal.
2.Platt calibration (Platt scaling)
Platt calibration ialah kaedah penentukuran klasifikasi yang agak tradisional berdasarkan model regresi logistik, yang sesuai dengan output rangkaian neural. Khususnya, penentukuran Platt memperkenalkan model regresi logistik binari untuk menyesuaikan output rangkaian saraf untuk mendapatkan taburan kebarangkalian baharu. Input model regresi logistik ialah output atau ciri rangkaian saraf, dan output ialah nilai kebarangkalian antara 0 dan 1. Dengan memasang model regresi logistik, nilai kebarangkalian yang diperbetulkan untuk setiap kategori boleh diperolehi.
Kelebihan penentukuran Platt ialah ia boleh menganggarkan kebarangkalian ramalan dengan lebih tepat dan sesuai untuk pelbagai masalah pengelasan yang berbeza. Walau bagaimanapun, penentukuran Platt memerlukan pemasangan model, jadi kos pengiraan adalah tinggi, dan sejumlah besar data berlabel diperlukan untuk melatih model regresi logistik.
2. Penentukuran regresi
Penentukuran regresi merujuk kepada membetulkan output model regresi untuk menjadikannya lebih dipercayai dan tepat. Dalam masalah regresi, output rangkaian saraf biasanya merupakan nilai sebenar berterusan yang mewakili nilai pembolehubah sasaran yang diramalkan. Walau bagaimanapun, nilai ramalan ini mungkin mempunyai bias atau varians, memerlukan penentukuran regresi untuk meningkatkan ketepatan dan kebolehpercayaan ramalan.
Kaedah penentukuran regresi yang biasa digunakan termasuk dua yang berikut:
1. Penentukuran Purata Sejarah
Penentukuran Purata Sejarah ialah penggunaan yang mudah dan berkesan, dan penentukuran datanya adalah teknologi yang mudah dan berkesan. min dan varians pembolehubah sasaran, dan kemudian laraskan nilai ramalan rangkaian saraf. Secara khusus, penentukuran purata sejarah memperoleh faktor penentukuran dengan mengira min dan varians data sejarah, dan kemudian membetulkan nilai ramalan rangkaian saraf untuk menjadikannya lebih dekat kepada nilai sasaran sebenar. Kelebihan penentukuran purata sejarah ialah ia mudah dan mudah digunakan, tidak memerlukan data latihan tambahan dan kos pengiraan, dan sesuai untuk pelbagai masalah regresi yang berbeza.
2. Penentukuran Regresi Linear
Penentukuran regresi linear ialah teknologi penentukuran regresi berdasarkan model regresi linear Prinsipnya adalah untuk memetakan nilai ramalan rangkaian saraf dengan menyesuaikan model nilai linear yang sebenar . Secara khusus, penentukuran regresi linear menggunakan data berlabel tambahan untuk melatih model regresi linear, mengambil nilai ramalan rangkaian saraf sebagai input dan nilai sasaran sebenar sebagai output untuk mendapatkan fungsi pemetaan linear, dengan itu melaksanakan ramalan pada ramalan rangkaian saraf. penentukuran.
Kelebihan penentukuran regresi linear ialah ia dapat menganggarkan hubungan antara nilai ramalan dan nilai sasaran dengan lebih tepat, dan sesuai untuk pelbagai masalah regresi. Walau bagaimanapun, pemasangan model regresi linear memerlukan sejumlah besar data berlabel dan kos pengiraan, dan mungkin tidak berkesan untuk masalah regresi dengan hubungan bukan linear.
Secara amnya, penentukuran klasifikasi dan penentukuran regresi ialah teknik penentukuran biasa dalam rangkaian saraf dalam, yang boleh meningkatkan prestasi dan kebolehpercayaan model. Penentukuran pengelasan terutamanya menjadikan kebarangkalian ramalan lebih tepat dengan melaraskan keyakinan pengelas penentukuran regresi terutamanya menjadikan hasil ramalan lebih dekat kepada nilai sasaran sebenar dengan membetulkan sisihan dan varians nilai ramalan. Dalam aplikasi praktikal, adalah perlu untuk memilih kaedah penentukuran yang sesuai berdasarkan masalah tertentu dan menggabungkannya dengan teknik lain untuk mengoptimumkan prestasi model.
Atas ialah kandungan terperinci Rangkaian saraf dalam untuk penentukuran klasifikasi dan penentukuran regresi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Membaca Indeks AI 2025: Adakah AI rakan, musuh, atau juruterbang bersama?Apr 11, 2025 pm 12:13 PM
Membaca Indeks AI 2025: Adakah AI rakan, musuh, atau juruterbang bersama?Apr 11, 2025 pm 12:13 PMLaporan Indeks Perisikan Buatan 2025 yang dikeluarkan oleh Stanford University Institute for Manusia Berorientasikan Kecerdasan Buatan memberikan gambaran yang baik tentang revolusi kecerdasan buatan yang berterusan. Mari kita menafsirkannya dalam empat konsep mudah: kognisi (memahami apa yang sedang berlaku), penghargaan (melihat faedah), penerimaan (cabaran muka), dan tanggungjawab (cari tanggungjawab kita). Kognisi: Kecerdasan buatan di mana -mana dan berkembang pesat Kita perlu menyedari betapa cepatnya kecerdasan buatan sedang berkembang dan menyebarkan. Sistem kecerdasan buatan sentiasa bertambah baik, mencapai hasil yang sangat baik dalam ujian matematik dan pemikiran kompleks, dan hanya setahun yang lalu mereka gagal dalam ujian ini. Bayangkan AI menyelesaikan masalah pengekodan kompleks atau masalah saintifik peringkat siswazah-sejak tahun 2023
 Bermula dengan Meta Llama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PM
Bermula dengan Meta Llama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PMMeta's Llama 3.2: Lompat ke hadapan dalam Multimodal dan Mobile AI META baru -baru ini melancarkan Llama 3.2, kemajuan yang ketara dalam AI yang memaparkan keupayaan penglihatan yang kuat dan model teks ringan yang dioptimumkan untuk peranti mudah alih. Membina kejayaan o
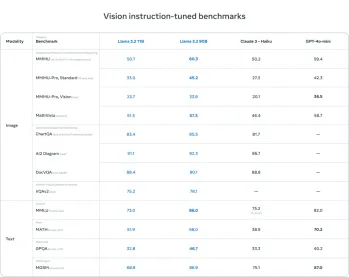 AV Bytes: Meta ' s llama 3.2, Google's Gemini 1.5, dan banyak lagiApr 11, 2025 pm 12:01 PM
AV Bytes: Meta ' s llama 3.2, Google's Gemini 1.5, dan banyak lagiApr 11, 2025 pm 12:01 PMLandskap AI minggu ini: Badai kemajuan, pertimbangan etika, dan perdebatan pengawalseliaan. Pemain utama seperti Openai, Google, Meta, dan Microsoft telah melepaskan kemas kini, dari model baru yang terobosan ke peralihan penting di LE
 Kos manusia bercakap dengan mesin: Bolehkah chatbot benar -benar peduli?Apr 11, 2025 pm 12:00 PM
Kos manusia bercakap dengan mesin: Bolehkah chatbot benar -benar peduli?Apr 11, 2025 pm 12:00 PMIlusi yang menghiburkan sambungan: Adakah kita benar -benar berkembang dalam hubungan kita dengan AI? Soalan ini mencabar nada optimis Simposium MIT Media Lab "yang memajukan AI (AHA)". Manakala acara itu mempamerkan cutting-EDG
 Memahami Perpustakaan Scipy di PythonApr 11, 2025 am 11:57 AM
Memahami Perpustakaan Scipy di PythonApr 11, 2025 am 11:57 AMPengenalan Bayangkan anda seorang saintis atau jurutera menangani masalah kompleks - persamaan pembezaan, cabaran pengoptimuman, atau analisis Fourier. Kemudahan penggunaan dan kemampuan grafik Python menarik, tetapi tugas -tugas ini menuntut alat yang berkuasa
 3 Kaedah untuk menjalankan Llama 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AM
3 Kaedah untuk menjalankan Llama 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AMMeta's Llama 3.2: Powerhouse AI Multimodal Model multimodal terbaru Meta, Llama 3.2, mewakili kemajuan yang ketara dalam AI, yang membanggakan pemahaman bahasa yang dipertingkatkan, ketepatan yang lebih baik, dan keupayaan penjanaan teks yang unggul. Keupayaannya t
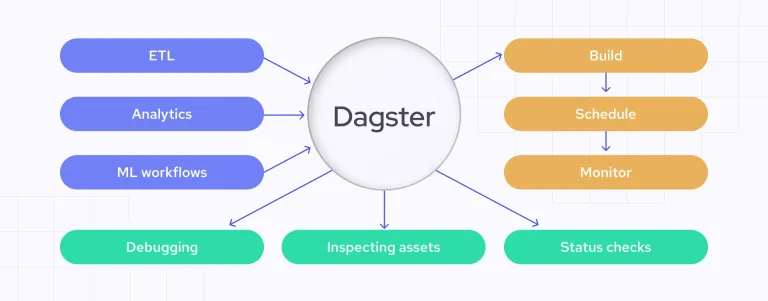 Mengotomatisasi Pemeriksaan Kualiti Data dengan DagsterApr 11, 2025 am 11:44 AM
Mengotomatisasi Pemeriksaan Kualiti Data dengan DagsterApr 11, 2025 am 11:44 AMJaminan Kualiti Data: Pemeriksaan Automatik dengan Dagster dan Harapan Hebat Mengekalkan kualiti data yang tinggi adalah penting untuk perniagaan yang didorong data. Apabila jumlah data dan sumber meningkat, kawalan kualiti manual menjadi tidak cekap dan terdedah kepada kesilapan.
 Adakah kerangka utama mempunyai peranan dalam era AI?Apr 11, 2025 am 11:42 AM
Adakah kerangka utama mempunyai peranan dalam era AI?Apr 11, 2025 am 11:42 AMMain Frames: Wira Unsung Revolusi AI Walaupun pelayan cemerlang dalam aplikasi tujuan umum dan mengendalikan pelbagai pelanggan, kerangka utama dibina untuk tugas tinggi, misi kritikal. Sistem yang kuat ini sering dijumpai di Heavil


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

SecLists
SecLists ialah rakan penguji keselamatan muktamad. Ia ialah koleksi pelbagai jenis senarai yang kerap digunakan semasa penilaian keselamatan, semuanya di satu tempat. SecLists membantu menjadikan ujian keselamatan lebih cekap dan produktif dengan menyediakan semua senarai yang mungkin diperlukan oleh penguji keselamatan dengan mudah. Jenis senarai termasuk nama pengguna, kata laluan, URL, muatan kabur, corak data sensitif, cangkerang web dan banyak lagi. Penguji hanya boleh menarik repositori ini ke mesin ujian baharu dan dia akan mempunyai akses kepada setiap jenis senarai yang dia perlukan.

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

EditPlus versi Cina retak
Saiz kecil, penyerlahan sintaks, tidak menyokong fungsi gesaan kod

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

VSCode Windows 64-bit Muat Turun
Editor IDE percuma dan berkuasa yang dilancarkan oleh Microsoft





