Rumah >pembangunan bahagian belakang >Tutorial Python >Penjelasan terperinci algoritma Bellman Ford dan pelaksanaan dalam Python
Penjelasan terperinci algoritma Bellman Ford dan pelaksanaan dalam Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2024-01-22 19:39:131336semak imbas
Algoritma Bellman Ford boleh mencari laluan terpendek dari nod sasaran ke nod lain dalam graf berwajaran. Ini sangat serupa dengan algoritma Dijkstra Algoritma Bellman-Ford boleh mengendalikan graf dengan pemberat negatif dan agak mudah dari segi pelaksanaan.
Penjelasan terperinci tentang prinsip algoritma Bellman Ford
Algoritma Bellman Ford secara berulang mencari laluan baharu yang lebih pendek daripada laluan yang terlebih anggaran dengan menganggarkan panjang laluan dari bucu permulaan kepada semua bucu lain.
Oleh kerana kita ingin merekodkan jarak laluan setiap nod, kita boleh menyimpannya dalam susunan saiz n, n juga mewakili bilangan nod. .
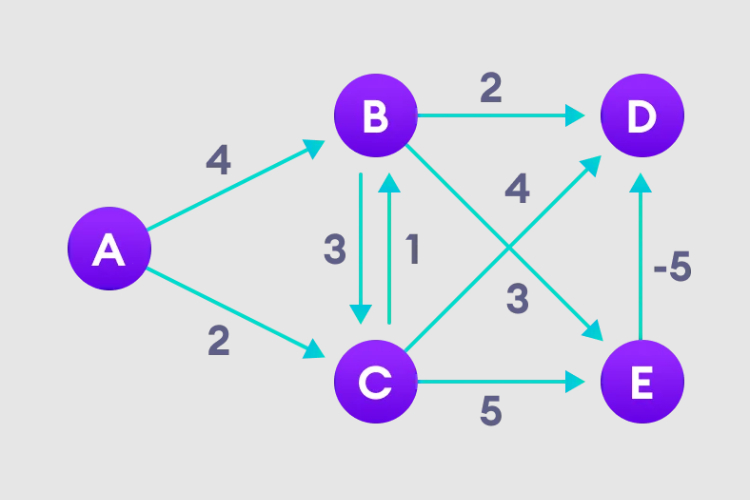
2. Lawati setiap tepi dan lakukan operasi kelonggaran untuk terus mengemas kini laluan terpendek.
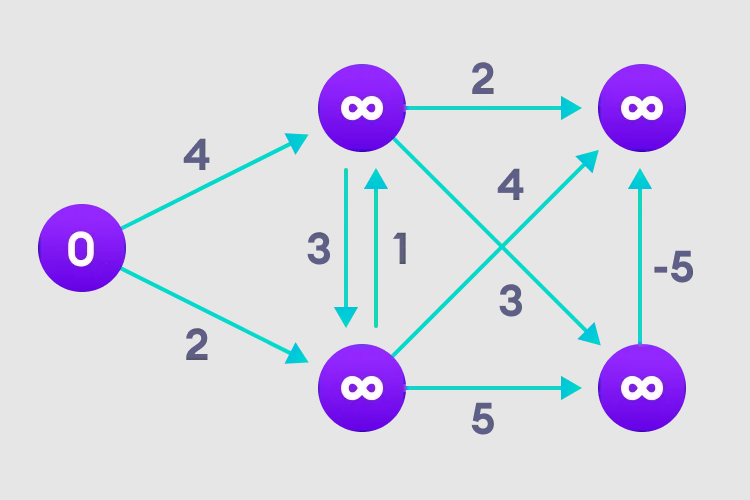
3 Kita perlu melakukan ini N-1 kali, kerana dalam kes yang paling teruk, panjang laluan nod terpendek mungkin perlu dilaraskan semula N-1 kali.
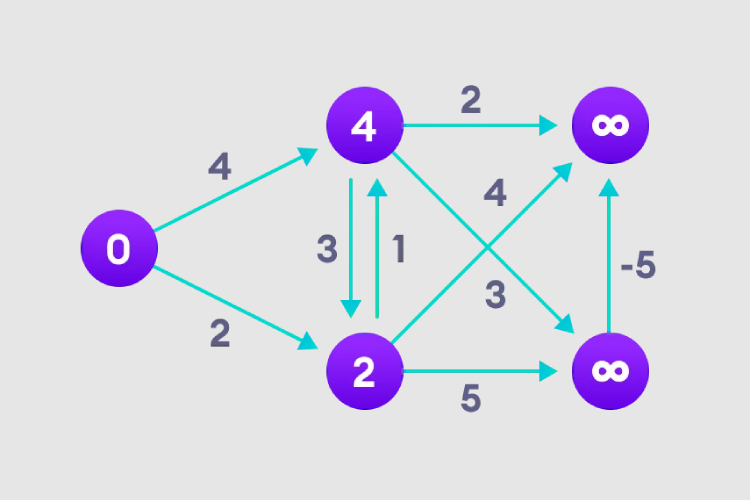
4. Perhatikan cara nod di penjuru kanan sebelah atas melaraskan panjang laluannya.
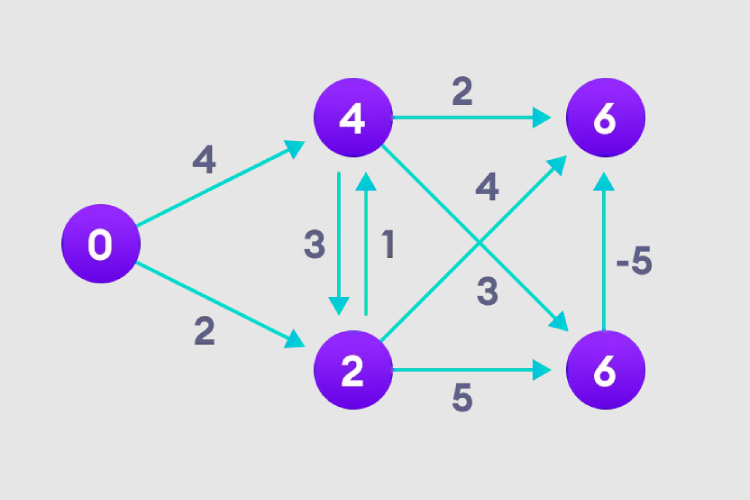
5. Selepas semua nod mempunyai panjang laluan, semak sama ada terdapat gelung negatif.
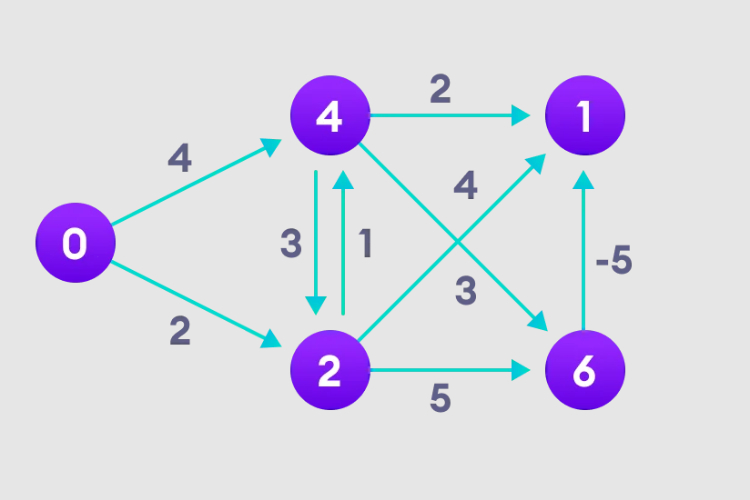
Python melaksanakan algoritma Bellman Ford
class Graph:
def __init__(self, vertices):
self.V = vertices # Total number of vertices in the graph
self.graph = [] # Array of edges
def add_edge(self, s, d, w):
self.graph.append([s, d, w])
def print_solution(self, dist):
print("Vertex Distance from Source")
for i in range(self.V):
print("{0}\t\t{1}".format(i, dist[i]))
def bellman_ford(self, src):
dist = [float("Inf")] * self.V
dist[src] = 0
for _ in range(self.V - 1):
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
dist[d] = dist[s] + w
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
print("Graph contains negative weight cycle")
return
self.print_solution(dist)
g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)
g.bellman_ford(0)Atas ialah kandungan terperinci Penjelasan terperinci algoritma Bellman Ford dan pelaksanaan dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

