 Peranti teknologi
Peranti teknologi AI
AI Pengenalan kepada Penguraian Nilai Tunggal (SVD) dan contoh-contohnya dalam pemampatan imej
Pengenalan kepada Penguraian Nilai Tunggal (SVD) dan contoh-contohnya dalam pemampatan imejPengenalan kepada Penguraian Nilai Tunggal (SVD) dan contoh-contohnya dalam pemampatan imej

Penguraian nilai tunggal (SVD) ialah kaedah yang digunakan untuk pemfaktoran matriks. Ia menguraikan matriks kepada hasil darab tiga matriks, iaitu matriks vektor tunggal kiri, matriks vektor tunggal kanan dan matriks nilai tunggal. SVD digunakan secara meluas dalam pengurangan dimensi data, pemprosesan isyarat, sistem pengesyoran dan bidang lain. Melalui SVD, kami boleh mengurangkan data berdimensi tinggi kepada ruang berdimensi rendah untuk mengekstrak ciri utama data. Dalam pemprosesan isyarat, SVD boleh digunakan untuk pengurangan hingar dan pembinaan semula isyarat. Dalam sistem pengesyoran, SVD boleh membantu kami menemui perkaitan tersembunyi antara pengguna dan item untuk membuat pengesyoran yang tepat. Ringkasnya, SVD ialah kaedah penguraian matriks yang berkuasa dan fleksibel yang menyelesaikan banyak masalah bagi kami SVD ialah singkatan penguraian nilai tunggal, yang menguraikan matriks kepada tiga bahagian: U, Σ dan V^T. Antaranya, U ialah matriks m×m, dan setiap lajur ialah vektor eigen bagi matriks AA^T, yang dipanggil vektor tunggal kiri V ialah matriks n×n, dan setiap lajur ialah vektor eigen bagi matriks A ^TA. , dipanggil vektor tunggal kanan Σ ialah matriks m×n, dan unsur-unsur pada pepenjurunya dipanggil nilai tunggal Ia adalah punca kuasa dua bagi nilai eigen bukan sifar bagi matriks AA^T dan A^TA. Melalui penguraian SVD, kami boleh membuka matriks kompleks kepada bahagian mudah untuk lebih memahami dan memproses data.
SVD ialah kaedah penguraian matriks yang biasa digunakan yang boleh digunakan untuk pemampatan matriks dan pengurangan dimensi. Ia menghampiri matriks asal dengan mengekalkan sebahagian besar nilai tunggal, dengan itu mengurangkan penyimpanan dan kerumitan pengiraan matriks. Selain itu, SVD juga boleh digunakan pada sistem pengesyoran. Dengan melakukan penguraian SVD pada pengguna dan matriks penilaian item, kami boleh mendapatkan vektor tersembunyi pengguna dan item. Vektor terpendam ini boleh menangkap potensi hubungan antara pengguna dan item, dengan itu memberikan hasil pengesyoran yang tepat untuk sistem pengesyoran.
Dalam aplikasi praktikal, kerumitan pengiraan SVD adalah tinggi, jadi teknik pengoptimuman perlu digunakan untuk mempercepatkan pengiraan, seperti SVD terpenggal dan SVD rawak. Teknologi ini boleh mengurangkan jumlah pengiraan dan meningkatkan kecekapan pengiraan.
Truncation SVD merujuk kepada mengekalkan bahagian dengan nilai singular yang lebih besar dan menetapkan nilai singular yang lebih kecil kepada sifar untuk mencapai mampatan matriks dan pengurangan dimensi. Stochastic SVD menghampiri penguraian SVD melalui unjuran rawak untuk mempercepatkan pengiraan.
SVD juga mempunyai beberapa bentuk lanjutan, seperti SVD berwajaran, SVD tambahan, SVD teragih, dll., yang boleh digunakan pada senario yang lebih kompleks.
SVD berwajaran memperkenalkan pemberat berdasarkan SVD standard untuk melakukan penguraian berwajaran matriks untuk menyesuaikan diri dengan lebih baik kepada keperluan aplikasi praktikal.
Incremental SVD merujuk kepada mengemas kini matriks secara berperingkat berdasarkan hasil penguraian SVD asal, dengan itu mengelakkan overhed pengiraan semula SVD setiap kali.
SVD teragih merujuk kepada pengagihan pengiraan penguraian SVD kepada berbilang komputer untuk mempercepatkan pengiraan dan sesuai untuk memproses data berskala besar.
SVD digunakan secara meluas dalam pembelajaran mesin, sistem pengesyoran, pemprosesan imej dan bidang lain, dan merupakan alat analisis data yang penting. Perkara di atas menerangkan prinsip dan teknik pengoptimuman penguraian nilai tunggal, dan kemudian mari kita lihat pada aplikasi praktikal penguraian nilai tunggal.
Cara menggunakan penguraian nilai tunggal untuk pemampatan imej
Idea asas menggunakan penguraian nilai tunggal untuk pemampatan imej adalah untuk menguraikan matriks imej melalui SVD, dan kemudian hanya mengekalkan beberapa nilai tunggal yang lebih besar dan vektor tunggal kiri dan kanan yang sepadan, Dengan itu mencapai pemampatan imej.
Langkah-langkah khusus adalah seperti berikut:
1. Tukar imej berwarna kepada imej skala kelabu dan dapatkan matriks A.
2. Lakukan penguraian SVD pada matriks A untuk mendapatkan tiga matriks U, S, dan V, di mana S ialah matriks pepenjuru dan unsur-unsur pada pepenjuru ialah nilai tunggal.
3 Hanya kekalkan nilai tunggal yang lebih besar dalam matriks S dan vektor tunggal kiri dan kanan yang sepadan untuk mendapatkan matriks baharu S', U', dan V'.
4. Darabkan S', U', dan V' untuk mendapatkan anggaran matriks A', dan gantikan matriks A asal dengan A-A', yang mencapai pemampatan.
Secara khusus, dalam langkah 3, bilangan k nilai tunggal yang akan dikekalkan perlu ditentukan mengikut nisbah mampatan dan keperluan kualiti imej Dalam keadaan biasa, mengekalkan 20-30 nilai tunggal pertama boleh mencapai kesan mampatan yang lebih baik. Pada masa yang sama, untuk mencapai kesan mampatan yang lebih baik, nilai tunggal yang dikekalkan boleh dikuantisasi dan dikodkan.
Perlu diambil perhatian bahawa semasa proses pemampatan imej menggunakan penguraian nilai tunggal, sejumlah maklumat imej mungkin hilang, jadi pertukaran perlu dibuat antara nisbah mampatan dan kualiti imej.
Atas ialah kandungan terperinci Pengenalan kepada Penguraian Nilai Tunggal (SVD) dan contoh-contohnya dalam pemampatan imej. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Membaca Indeks AI 2025: Adakah AI rakan, musuh, atau juruterbang bersama?Apr 11, 2025 pm 12:13 PM
Membaca Indeks AI 2025: Adakah AI rakan, musuh, atau juruterbang bersama?Apr 11, 2025 pm 12:13 PMLaporan Indeks Perisikan Buatan 2025 yang dikeluarkan oleh Stanford University Institute for Manusia Berorientasikan Kecerdasan Buatan memberikan gambaran yang baik tentang revolusi kecerdasan buatan yang berterusan. Mari kita menafsirkannya dalam empat konsep mudah: kognisi (memahami apa yang sedang berlaku), penghargaan (melihat faedah), penerimaan (cabaran muka), dan tanggungjawab (cari tanggungjawab kita). Kognisi: Kecerdasan buatan di mana -mana dan berkembang pesat Kita perlu menyedari betapa cepatnya kecerdasan buatan sedang berkembang dan menyebarkan. Sistem kecerdasan buatan sentiasa bertambah baik, mencapai hasil yang sangat baik dalam ujian matematik dan pemikiran kompleks, dan hanya setahun yang lalu mereka gagal dalam ujian ini. Bayangkan AI menyelesaikan masalah pengekodan kompleks atau masalah saintifik peringkat siswazah-sejak tahun 2023
 Bermula dengan Meta Llama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PM
Bermula dengan Meta Llama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PMMeta's Llama 3.2: Lompat ke hadapan dalam Multimodal dan Mobile AI META baru -baru ini melancarkan Llama 3.2, kemajuan yang ketara dalam AI yang memaparkan keupayaan penglihatan yang kuat dan model teks ringan yang dioptimumkan untuk peranti mudah alih. Membina kejayaan o
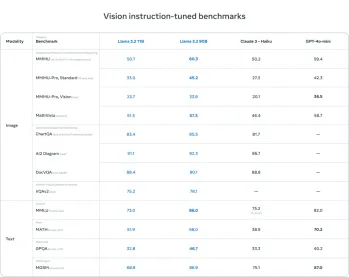 AV Bytes: Meta ' s llama 3.2, Google's Gemini 1.5, dan banyak lagiApr 11, 2025 pm 12:01 PM
AV Bytes: Meta ' s llama 3.2, Google's Gemini 1.5, dan banyak lagiApr 11, 2025 pm 12:01 PMLandskap AI minggu ini: Badai kemajuan, pertimbangan etika, dan perdebatan pengawalseliaan. Pemain utama seperti Openai, Google, Meta, dan Microsoft telah melepaskan kemas kini, dari model baru yang terobosan ke peralihan penting di LE
 Kos manusia bercakap dengan mesin: Bolehkah chatbot benar -benar peduli?Apr 11, 2025 pm 12:00 PM
Kos manusia bercakap dengan mesin: Bolehkah chatbot benar -benar peduli?Apr 11, 2025 pm 12:00 PMIlusi yang menghiburkan sambungan: Adakah kita benar -benar berkembang dalam hubungan kita dengan AI? Soalan ini mencabar nada optimis Simposium MIT Media Lab "yang memajukan AI (AHA)". Manakala acara itu mempamerkan cutting-EDG
 Memahami Perpustakaan Scipy di PythonApr 11, 2025 am 11:57 AM
Memahami Perpustakaan Scipy di PythonApr 11, 2025 am 11:57 AMPengenalan Bayangkan anda seorang saintis atau jurutera menangani masalah kompleks - persamaan pembezaan, cabaran pengoptimuman, atau analisis Fourier. Kemudahan penggunaan dan kemampuan grafik Python menarik, tetapi tugas -tugas ini menuntut alat yang berkuasa
 3 Kaedah untuk menjalankan Llama 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AM
3 Kaedah untuk menjalankan Llama 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AMMeta's Llama 3.2: Powerhouse AI Multimodal Model multimodal terbaru Meta, Llama 3.2, mewakili kemajuan yang ketara dalam AI, yang membanggakan pemahaman bahasa yang dipertingkatkan, ketepatan yang lebih baik, dan keupayaan penjanaan teks yang unggul. Keupayaannya t
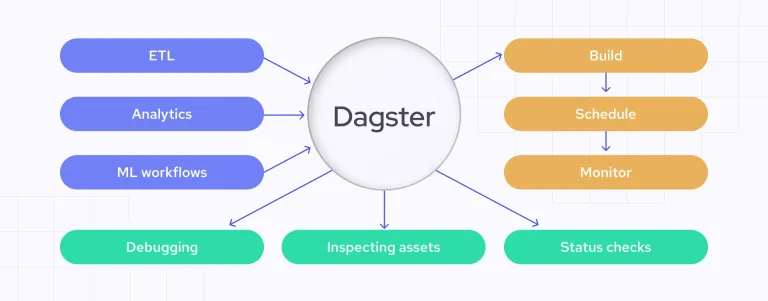 Mengotomatisasi Pemeriksaan Kualiti Data dengan DagsterApr 11, 2025 am 11:44 AM
Mengotomatisasi Pemeriksaan Kualiti Data dengan DagsterApr 11, 2025 am 11:44 AMJaminan Kualiti Data: Pemeriksaan Automatik dengan Dagster dan Harapan Hebat Mengekalkan kualiti data yang tinggi adalah penting untuk perniagaan yang didorong data. Apabila jumlah data dan sumber meningkat, kawalan kualiti manual menjadi tidak cekap dan terdedah kepada kesilapan.
 Adakah kerangka utama mempunyai peranan dalam era AI?Apr 11, 2025 am 11:42 AM
Adakah kerangka utama mempunyai peranan dalam era AI?Apr 11, 2025 am 11:42 AMMain Frames: Wira Unsung Revolusi AI Walaupun pelayan cemerlang dalam aplikasi tujuan umum dan mengendalikan pelbagai pelanggan, kerangka utama dibina untuk tugas tinggi, misi kritikal. Sistem yang kuat ini sering dijumpai di Heavil


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

mPDF
mPDF ialah perpustakaan PHP yang boleh menjana fail PDF daripada HTML yang dikodkan UTF-8. Pengarang asal, Ian Back, menulis mPDF untuk mengeluarkan fail PDF "dengan cepat" dari tapak webnya dan mengendalikan bahasa yang berbeza. Ia lebih perlahan dan menghasilkan fail yang lebih besar apabila menggunakan fon Unicode daripada skrip asal seperti HTML2FPDF, tetapi menyokong gaya CSS dsb. dan mempunyai banyak peningkatan. Menyokong hampir semua bahasa, termasuk RTL (Arab dan Ibrani) dan CJK (Cina, Jepun dan Korea). Menyokong elemen peringkat blok bersarang (seperti P, DIV),

DVWA
Damn Vulnerable Web App (DVWA) ialah aplikasi web PHP/MySQL yang sangat terdedah. Matlamat utamanya adalah untuk menjadi bantuan bagi profesional keselamatan untuk menguji kemahiran dan alatan mereka dalam persekitaran undang-undang, untuk membantu pembangun web lebih memahami proses mengamankan aplikasi web, dan untuk membantu guru/pelajar mengajar/belajar dalam persekitaran bilik darjah Aplikasi web keselamatan. Matlamat DVWA adalah untuk mempraktikkan beberapa kelemahan web yang paling biasa melalui antara muka yang mudah dan mudah, dengan pelbagai tahap kesukaran. Sila ambil perhatian bahawa perisian ini

SecLists
SecLists ialah rakan penguji keselamatan muktamad. Ia ialah koleksi pelbagai jenis senarai yang kerap digunakan semasa penilaian keselamatan, semuanya di satu tempat. SecLists membantu menjadikan ujian keselamatan lebih cekap dan produktif dengan menyediakan semua senarai yang mungkin diperlukan oleh penguji keselamatan dengan mudah. Jenis senarai termasuk nama pengguna, kata laluan, URL, muatan kabur, corak data sensitif, cangkerang web dan banyak lagi. Penguji hanya boleh menarik repositori ini ke mesin ujian baharu dan dia akan mempunyai akses kepada setiap jenis senarai yang dia perlukan.

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

MinGW - GNU Minimalis untuk Windows
Projek ini dalam proses untuk dipindahkan ke osdn.net/projects/mingw, anda boleh terus mengikuti kami di sana. MinGW: Port Windows asli bagi GNU Compiler Collection (GCC), perpustakaan import yang boleh diedarkan secara bebas dan fail pengepala untuk membina aplikasi Windows asli termasuk sambungan kepada masa jalan MSVC untuk menyokong fungsi C99. Semua perisian MinGW boleh dijalankan pada platform Windows 64-bit.





