Rumah >pangkalan data >tutorial mysql >Penjelasan terperinci tentang operasi pemadaman B-tree: Ilustrasi terperinci operasi pemadaman B-tree menggunakan Python
Penjelasan terperinci tentang operasi pemadaman B-tree: Ilustrasi terperinci operasi pemadaman B-tree menggunakan Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2024-01-22 14:27:091154semak imbas
Operasi pemadaman B-tree perlu mengambil kira lokasi dan keseimbangan nod, dan aliran bawah berkemungkinan berlaku. Aliran bawah berlaku apabila nod mengandungi kurang daripada bilangan minimum nod anak yang sepatutnya dipegangnya.
Gambar dan teks menunjukkan prinsip pemadaman B-tree
tanpa menjejaskan keseimbangan.
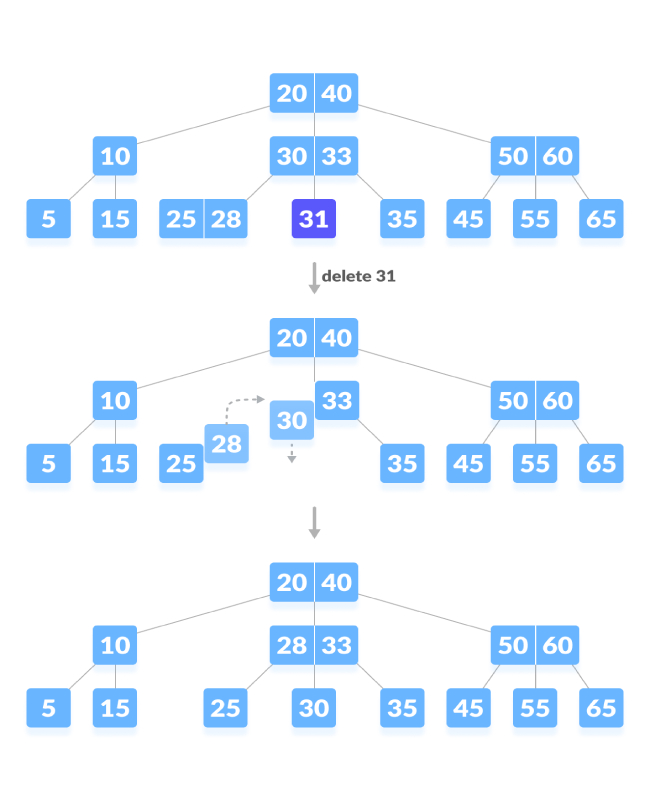
Situasi aliran bawah.
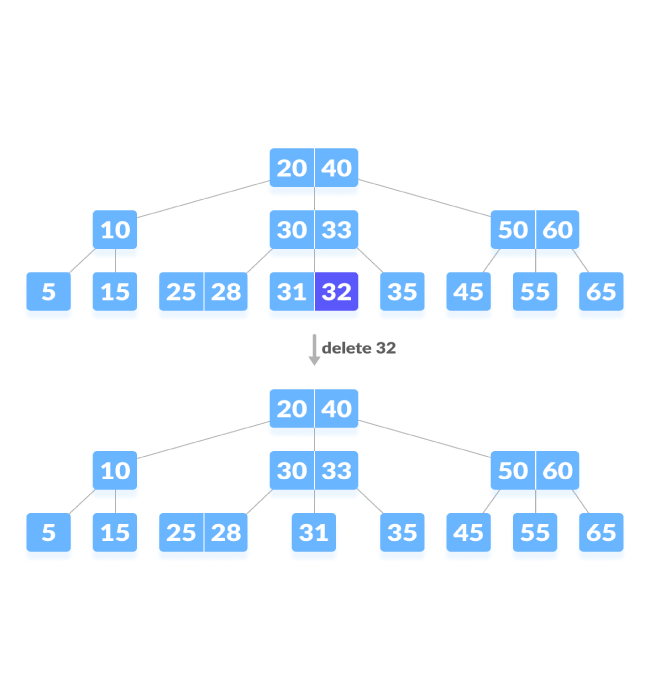
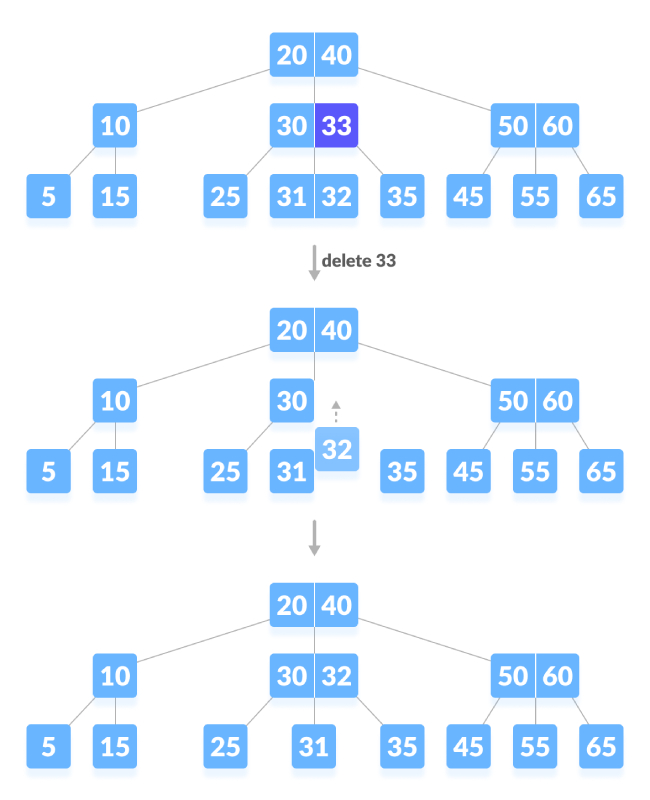
Padamkan nod dalaman.
Python melaksanakan operasi pemadaman B-tree
# B树节点
class BTreeNode:
def __init__(self, leaf=False):
self.leaf = leaf
self.keys = []
self.child = []
class BTree:
def __init__(self, t):
self.root = BTreeNode(True)
self.t = t
# 插入元素
def insert(self, k):
root = self.root
if len(root.keys) == (2 * self.t) - 1:
temp = BTreeNode()
self.root = temp
temp.child.insert(0, root)
self.split_child(temp, 0)
self.insert_non_full(temp, k)
else:
self.insert_non_full(root, k)
def insert_non_full(self, x, k):
i = len(x.keys) - 1
if x.leaf:
x.keys.append((None, None))
while i >= 0 and k[0] < x.keys[i][0]:
x.keys[i + 1] = x.keys[i]
i -= 1
x.keys[i + 1] = k
else:
while i >= 0 and k[0] < x.keys[i][0]:
i -= 1
i += 1
if len(x.child[i].keys) == (2 * self.t) - 1:
self.split_child(x, i)
if k[0] > x.keys[i][0]:
i += 1
self.insert_non_full(x.child[i], k)
# 分开子节点
def split_child(self, x, i):
t = self.t
y = x.child[i]
z = BTreeNode(y.leaf)
x.child.insert(i + 1, z)
x.keys.insert(i, y.keys[t - 1])
z.keys = y.keys[t: (2 * t) - 1]
y.keys = y.keys[0: t - 1]
if not y.leaf:
z.child = y.child[t: 2 * t]
y.child = y.child[0: t - 1]
# 删除节点
def delete(self, x, k):
t = self.t
i = 0
while i < len(x.keys) and k[0] > x.keys[i][0]:
i += 1
if x.leaf:
if i < len(x.keys) and x.keys[i][0] == k[0]:
x.keys.pop(i)
return
return
if i < len(x.keys) and x.keys[i][0] == k[0]:
return self.delete_internal_node(x, k, i)
elif len(x.child[i].keys) >= t:
self.delete(x.child[i], k)
else:
if i != 0 and i + 2 < len(x.child):
if len(x.child[i - 1].keys) >= t:
self.delete_sibling(x, i, i - 1)
elif len(x.child[i + 1].keys) >= t:
self.delete_sibling(x, i, i + 1)
else:
self.delete_merge(x, i, i + 1)
elif i == 0:
if len(x.child[i + 1].keys) >= t:
self.delete_sibling(x, i, i + 1)
else:
self.delete_merge(x, i, i + 1)
elif i + 1 == len(x.child):
if len(x.child[i - 1].keys) >= t:
self.delete_sibling(x, i, i - 1)
else:
self.delete_merge(x, i, i - 1)
self.delete(x.child[i], k)
# 删除节点
def delete_internal_node(self, x, k, i):
t = self.t
if x.leaf:
if x.keys[i][0] == k[0]:
x.keys.pop(i)
return
return
if len(x.child[i].keys) >= t:
x.keys[i] = self.delete_predecessor(x.child[i])
return
elif len(x.child[i + 1].keys) >= t:
x.keys[i] = self.delete_successor(x.child[i + 1])
return
else:
self.delete_merge(x, i, i + 1)
self.delete_internal_node(x.child[i], k, self.t - 1)
# 删除前节点
def delete_predecessor(self, x):
if x.leaf:
return x.pop()
n = len(x.keys) - 1
if len(x.child[n].keys) >= self.t:
self.delete_sibling(x, n + 1, n)
else:
self.delete_merge(x, n, n + 1)
self.delete_predecessor(x.child[n])
# 删除继任节点
def delete_successor(self, x):
if x.leaf:
return x.keys.pop(0)
if len(x.child[1].keys) >= self.t:
self.delete_sibling(x, 0, 1)
else:
self.delete_merge(x, 0, 1)
self.delete_successor(x.child[0])
def delete_merge(self, x, i, j):
cnode = x.child[i]
if j > i:
rsnode = x.child[j]
cnode.keys.append(x.keys[i])
for k in range(len(rsnode.keys)):
cnode.keys.append(rsnode.keys[k])
if len(rsnode.child) > 0:
cnode.child.append(rsnode.child[k])
if len(rsnode.child) > 0:
cnode.child.append(rsnode.child.pop())
new = cnode
x.keys.pop(i)
x.child.pop(j)
else:
lsnode = x.child[j]
lsnode.keys.append(x.keys[j])
for i in range(len(cnode.keys)):
lsnode.keys.append(cnode.keys[i])
if len(lsnode.child) > 0:
lsnode.child.append(cnode.child[i])
if len(lsnode.child) > 0:
lsnode.child.append(cnode.child.pop())
new = lsnode
x.keys.pop(j)
x.child.pop(i)
if x == self.root and len(x.keys) == 0:
self.root = new
# 删除同一级的其他子节点
def delete_sibling(self, x, i, j):
cnode = x.child[i]
if i < j:
rsnode = x.child[j]
cnode.keys.append(x.keys[i])
x.keys[i] = rsnode.keys[0]
if len(rsnode.child) > 0:
cnode.child.append(rsnode.child[0])
rsnode.child.pop(0)
rsnode.keys.pop(0)
else:
lsnode = x.child[j]
cnode.keys.insert(0, x.keys[i - 1])
x.keys[i - 1] = lsnode.keys.pop()
if len(lsnode.child) > 0:
cnode.child.insert(0, lsnode.child.pop())
# 输出B树
def print_tree(self, x, l=0):
print("Level ", l, " ", len(x.keys), end=":")
for i in x.keys:
print(i, end=" ")
print()
l += 1
if len(x.child) > 0:
for i in x.child:
self.print_tree(i, l)
B = BTree(3)
for i in range(10):
B.insert((i, 2 * i))
B.print_tree(B.root)
B.delete(B.root, (8,))
print("\n")
B.print_tree(B.root)Atas ialah kandungan terperinci Penjelasan terperinci tentang operasi pemadaman B-tree: Ilustrasi terperinci operasi pemadaman B-tree menggunakan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Kenyataan:
Artikel ini dikembalikan pada:163.com. Jika ada pelanggaran, sila hubungi admin@php.cn Padam
Artikel sebelumnya:Gunakan Python untuk menulis kod operasi pemadaman pokok B+Artikel seterusnya:Gunakan Python untuk menulis kod operasi pemadaman pokok B+

