Rumah >Peranti teknologi >AI >Tembusi halangan maklumat! Alat visualisasi 3D berskala besar yang mengejutkan dikeluarkan!
Tembusi halangan maklumat! Alat visualisasi 3D berskala besar yang mengejutkan dikeluarkan!
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2024-01-16 12:15:211137semak imbas
Baru-baru ini, seorang lelaki dari New Zealand, Brendan Bycroft, telah mencipta kegilaan dalam kalangan teknologi. Projek yang diciptanya dipanggil Visualisasi 3D Model Besar bukan sahaja mendahului senarai Berita Penggodam, tetapi kesannya yang mengejutkan adalah lebih mengejutkan. Melalui projek ini, anda akan memahami sepenuhnya cara LLM (Model Bahasa Besar) berfungsi dalam beberapa saat sahaja.
Sama ada anda peminat teknologi atau tidak, projek ini akan membawa anda pesta visual dan pencerahan kognitif yang belum pernah berlaku sebelum ini. Mari kita terokai ciptaan yang menakjubkan ini bersama-sama!
Pengenalan
Dalam projek ini, Bycroft menganalisis secara terperinci model GPT ringan yang dipanggil Nano-GPT yang dibangunkan oleh saintis OpenAI Andrej Karpathy. Sebagai versi pengurangan model GPT, model itu hanya mempunyai 85,000 parameter. Sudah tentu, walaupun model ini jauh lebih kecil daripada GPT-3 atau GPT-4 OpenAI, boleh dikatakan bahawa "burung pipit adalah kecil tetapi mempunyai semua organ dalaman."
Nano-GPT GitHub: https://github.com/karpathy/nanoGPT
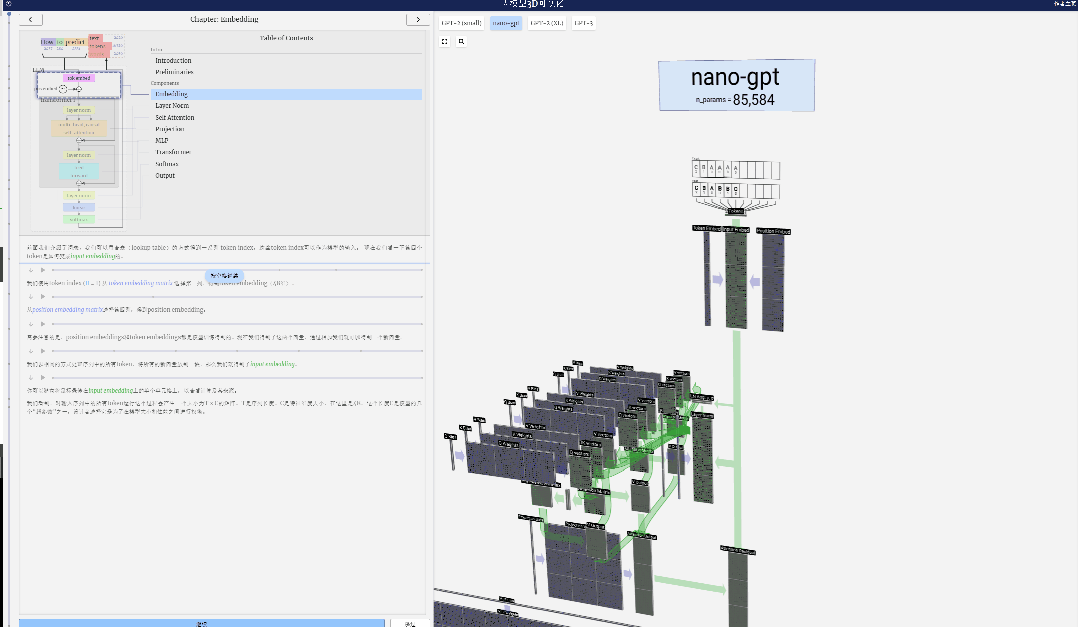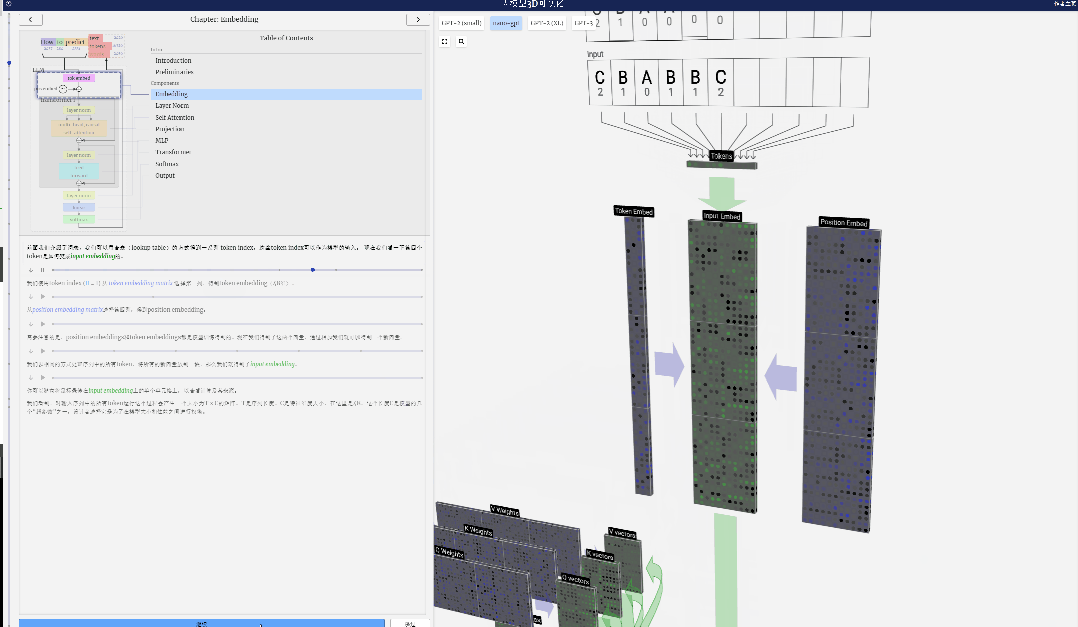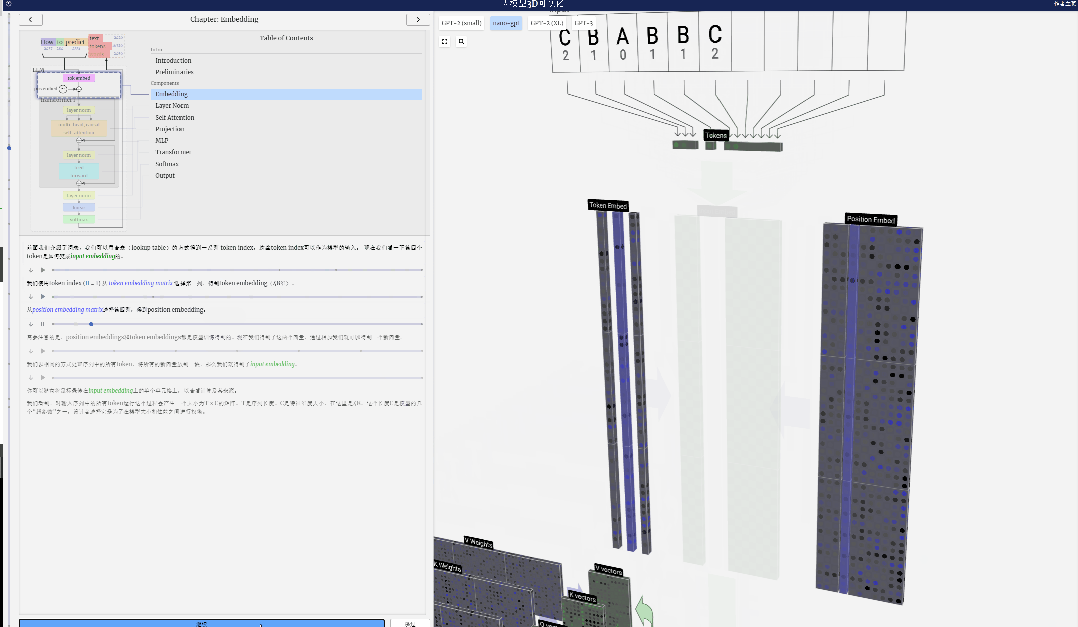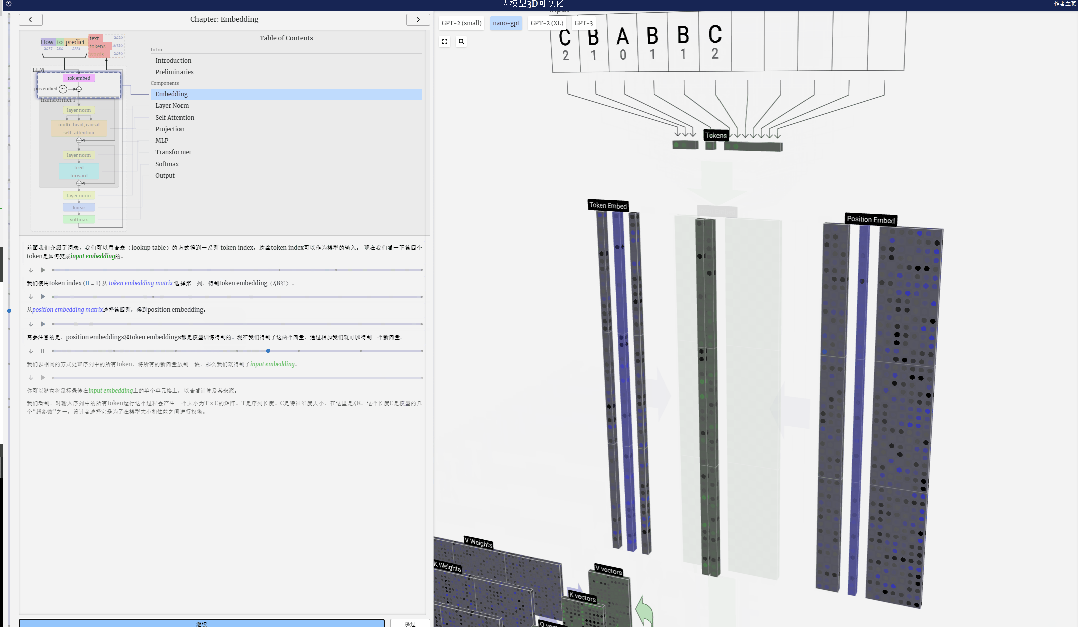
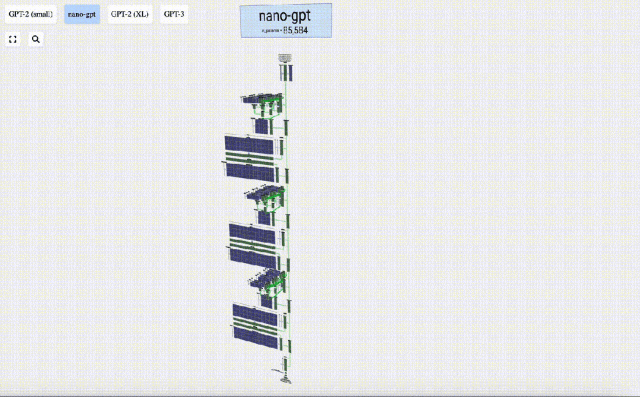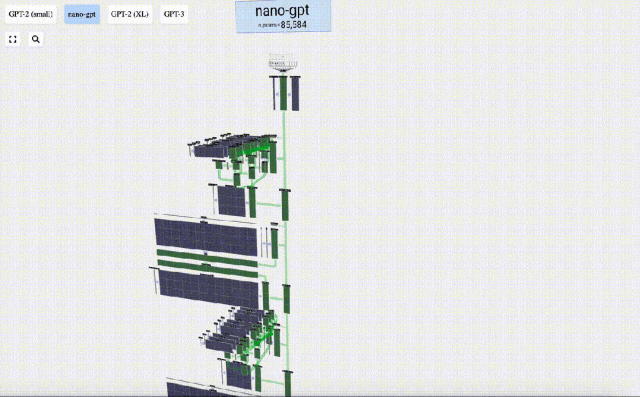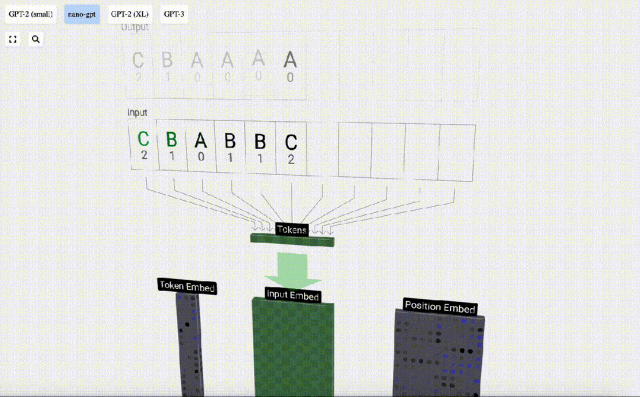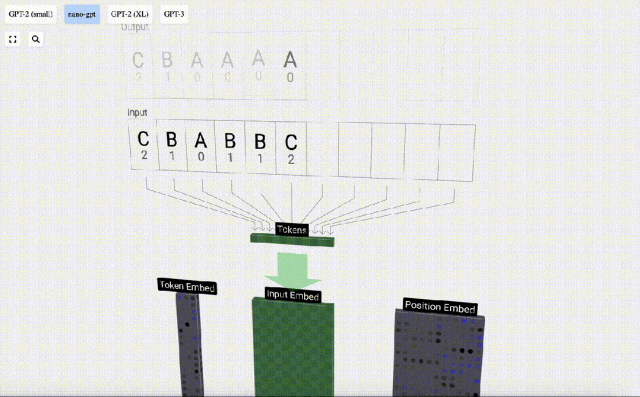
Untuk memudahkan demonstrasi setiap lapisan model Transformer, Bycroft mengatur tugas sasaran yang sangat mudah untuk model Nano-GPT: model input ialah 6 huruf "CBABBC", output ialah urutan yang disusun mengikut susunan abjad, contohnya, output "ABBBCC".
Kami memanggil setiap huruf sebagai token, dan huruf yang berbeza ini membentuk perbendaharaan kata:
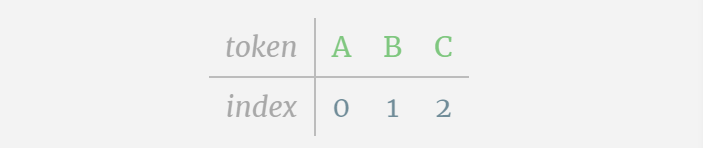
Untuk ini Untuk jadual, setiap huruf diberikan indeks token subskrip. Urutan yang terdiri daripada subskrip ini boleh digunakan sebagai input model: 2 1 0 1 1 2
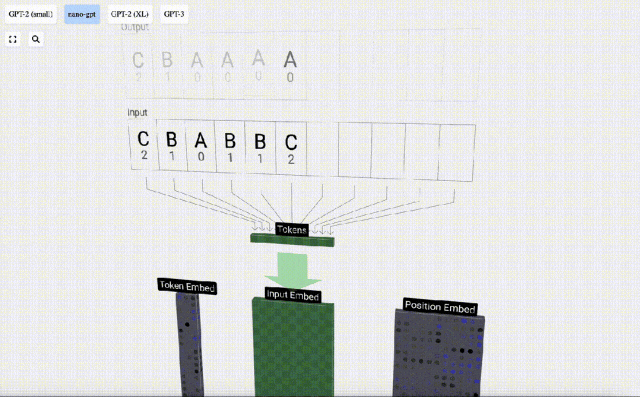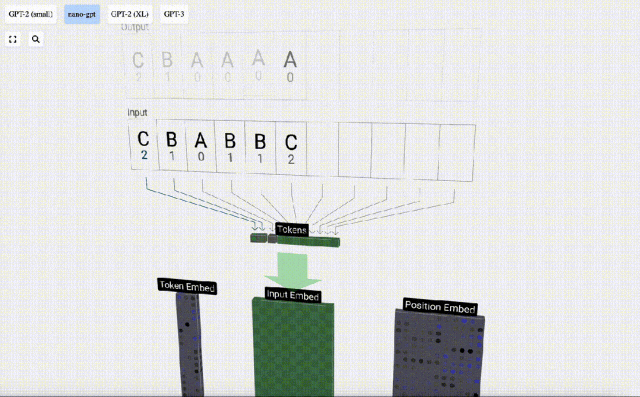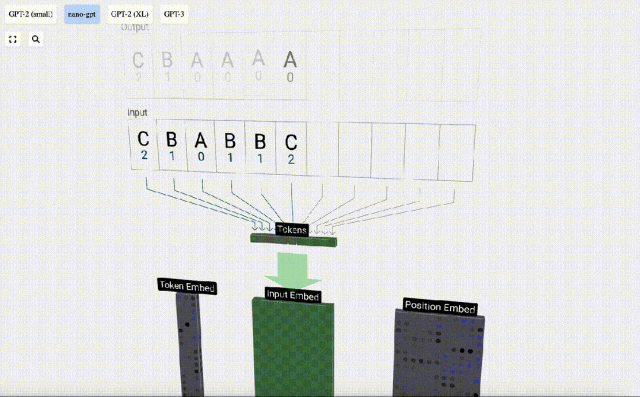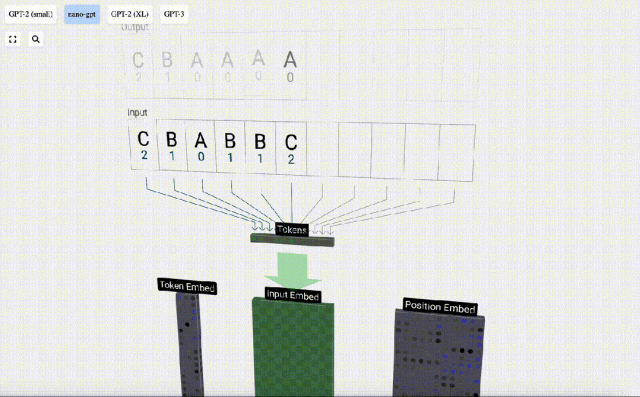
Dalam visualisasi 3D, setiap sel hijau mewakili nombor yang dikira, manakala setiap sel biru mewakili berat model .
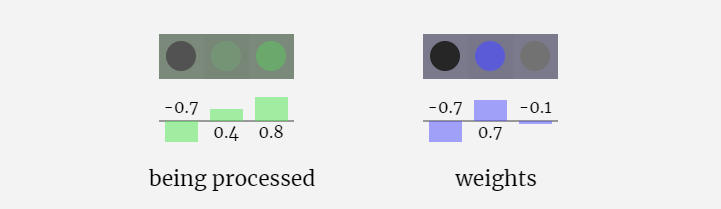
Dalam pemprosesan jujukan, setiap nombor mula-mula ditukar kepada vektor dimensi-C Proses ini dipanggil pembenaman. Dalam Nano-GPT, dimensi benam ini biasanya 48 dimensi. Melalui operasi pembenaman ini, setiap nombor diwakili sebagai vektor dalam ruang dimensi C, yang membolehkan pemprosesan dan analisis seterusnya yang lebih baik.
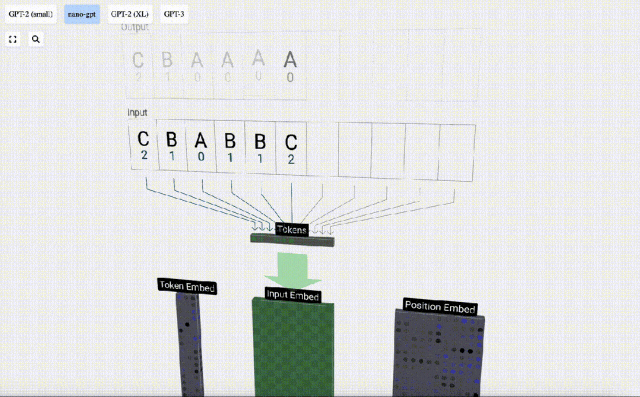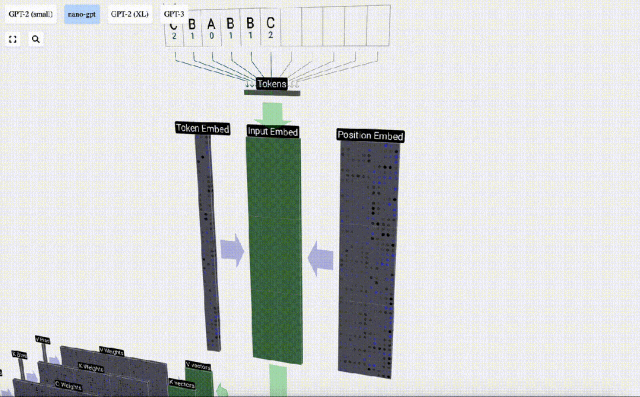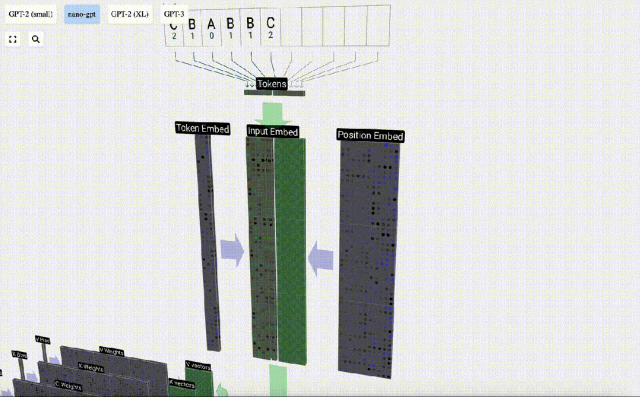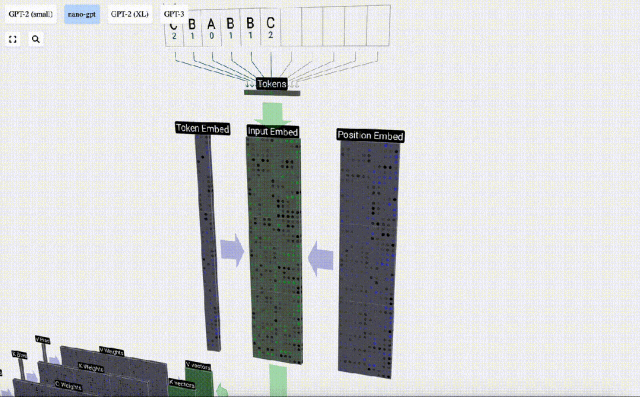
pembenaman dikira melalui satu siri lapisan model pertengahan, yang biasanya dipanggil Transformers, dan akhirnya sampai ke lapisan bawah.

"Jadi apakah outputnya?"
Output model ialah token seterusnya dalam jujukan. Jadi pada akhirnya, kita mendapat nilai kebarangkalian bahawa token seterusnya ialah A B C.
Dalam contoh ini, model kedudukan ke-6 mengeluarkan A dengan kebarangkalian yang tinggi. Sekarang kita boleh lulus A sebagai input kepada model dan ulangi keseluruhan proses.
Visualisasi GPT-2 dan GPT-3 juga ditunjukkan.
- GPT-3 mempunyai 175 bilion parameter, dan lapisan model mempunyai 8 lajur, padat meliputi keseluruhan skrin.
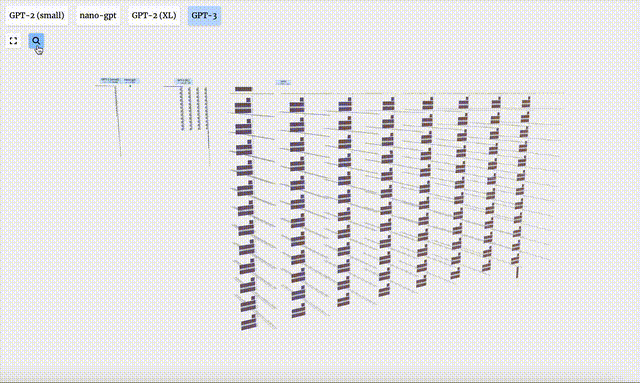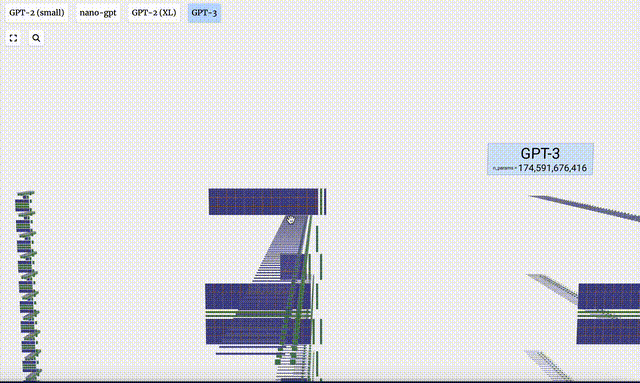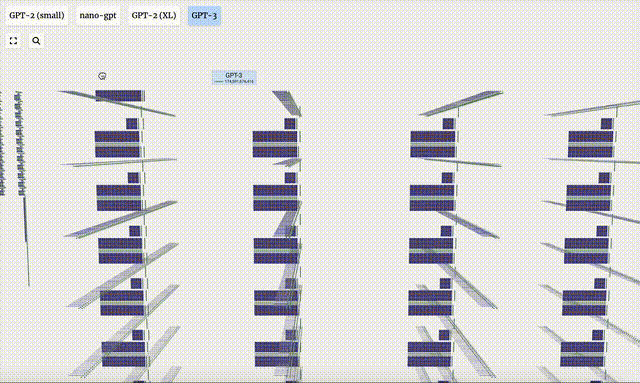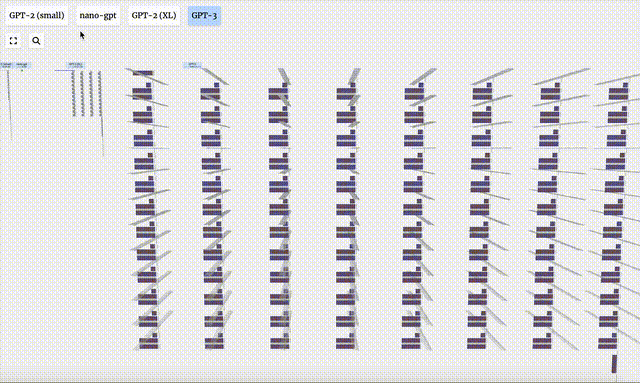
- Versi parameter yang berbeza bagi model GPT-2 menunjukkan perbezaan seni bina yang besar. Di sini kita mengambil 15 bilion parameter GPT-2 (XL) dan 124 juta parameter GPT-2 (Kecil) sebagai contoh.

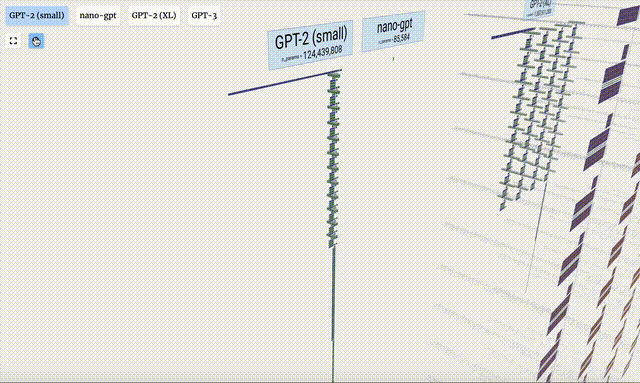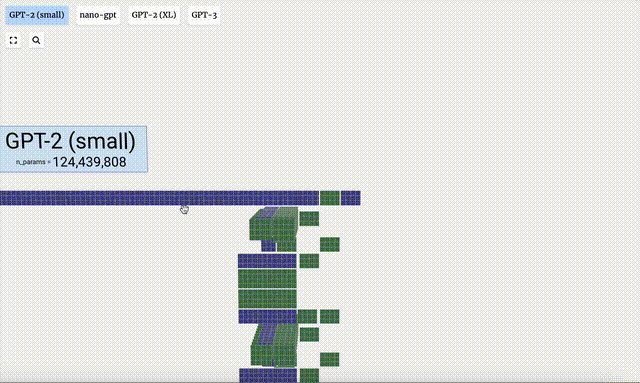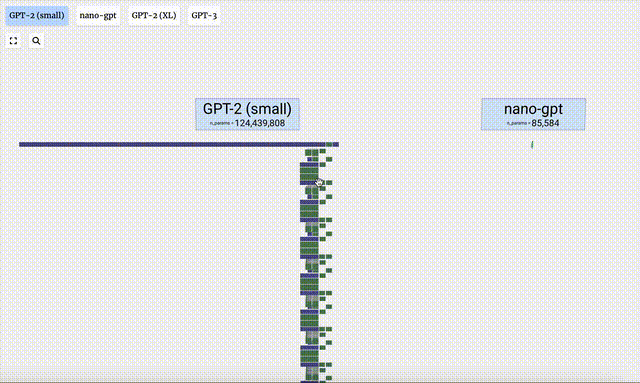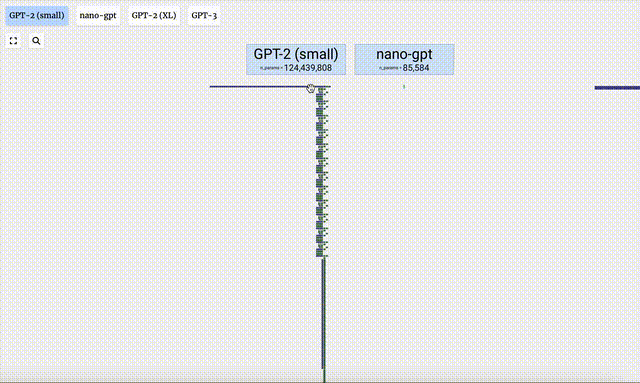
Perlu diambil perhatian bahawa visualisasi ini tertumpu terutamanya pada inferens model (inferens), bukan latihan, jadi ia hanya sebahagian kecil daripada keseluruhan proses pembelajaran mesin. Selain itu, diandaikan di sini bahawa pemberat model telah dilatih terlebih dahulu, dan kemudian inferens model digunakan untuk menjana output.
Membenamkan
Seperti yang dinyatakan sebelum ini, cara menggunakan jadual carian mudah untuk memetakan token kepada siri integer.
Integer ini, indeks token, adalah kali pertama dan satu-satunya kita melihat integer dalam model. Selepas itu, operasi akan dilakukan menggunakan nombor titik terapung (nombor perpuluhan).
Di sini, ambil token ke-4 (indeks 3) sebagai contoh untuk melihat cara ia digunakan untuk menjana vektor lajur ke-4 bagi pembenaman input.

Mula-mula gunakan indeks token (di sini, B=1 diambil sebagai contoh) untuk memilih lajur kedua daripada matriks Token Embedding dan dapatkan vektor lajur bersaiz C=48 (48 dimensi), yang dipanggil pembenaman token.

Kemudian pilih lajur keempat dari matriks benam kedudukan ("Kerana di sini kita terutamanya melihat (t = 3) token B pada kedudukan ke-4"), begitu juga, kita mendapat saiz C=48 (48). dimensi) Vektor lajur, dipanggil pembenaman kedudukan.

Perlu diingatkan bahawa benam kedudukan dan benam token kedua-duanya diperoleh melalui latihan model (ditandakan dengan warna biru). Sekarang kita mempunyai dua vektor ini, dengan menambahkannya kita boleh mendapatkan vektor lajur baharu bersaiz C=48.

Seterusnya, proses semua token dalam urutan dalam proses yang sama, mencipta satu set vektor yang mengandungi nilai token dan kedudukannya.

Seperti yang dapat dilihat dari rajah di atas, menjalankan proses ini pada semua token dalam urutan input akan menghasilkan matriks bersaiz TxC. Antaranya, T mewakili panjang jujukan. C bermaksud saluran, tetapi juga dipanggil ciri atau dimensi atau saiz benam, yang dalam kes ini ialah 48. Panjang C ini ialah salah satu daripada beberapa "hiperparameter" model, yang dipilih oleh pereka bentuk untuk menyediakan pertukaran antara saiz model dan prestasi.
Matriks dengan dimensi TxC ini ialah pembenaman input dan diturunkan melalui model.
Petua Sedikit: Sila tuding tetikus anda pada satu sel pada pembenaman input untuk melihat pengiraan dan sumbernya.
Lapisan Norm
Matriks benam input yang diperoleh sebelum ini ialah input lapisan Transformer.
Langkah pertama lapisan Transformer ialah melakukan penormalan lapisan pada matriks pemasukan input Ini adalah operasi untuk menormalkan nilai setiap lajur matriks input.
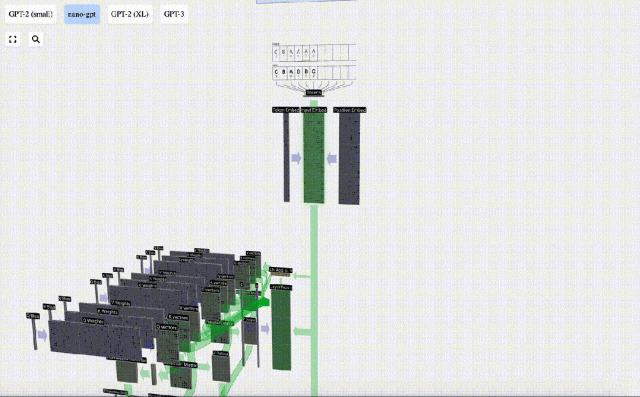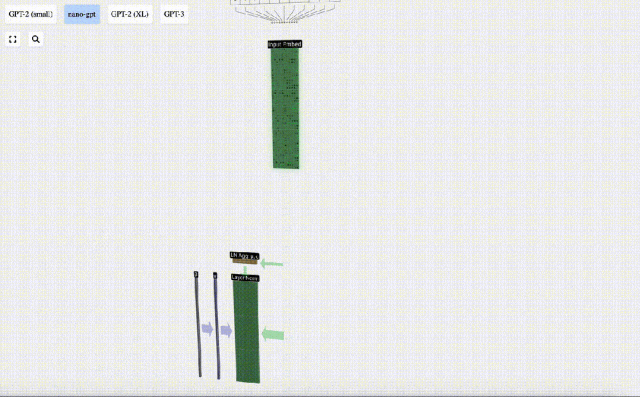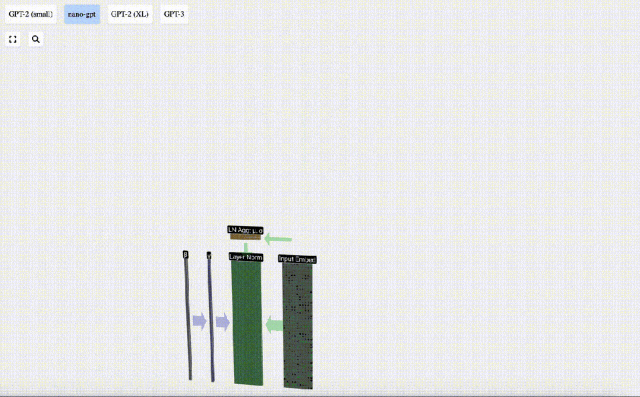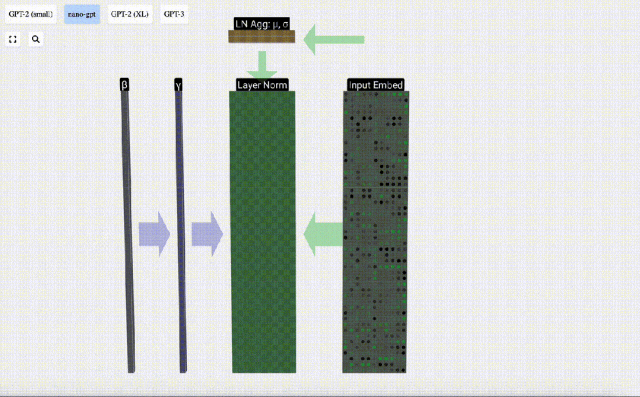
Penormalan ialah langkah penting dalam latihan rangkaian saraf dalam, yang membantu meningkatkan kestabilan model semasa proses latihan.
Kita boleh melihat lajur matriks secara berasingan Lajur keempat diambil sebagai contoh di bawah.
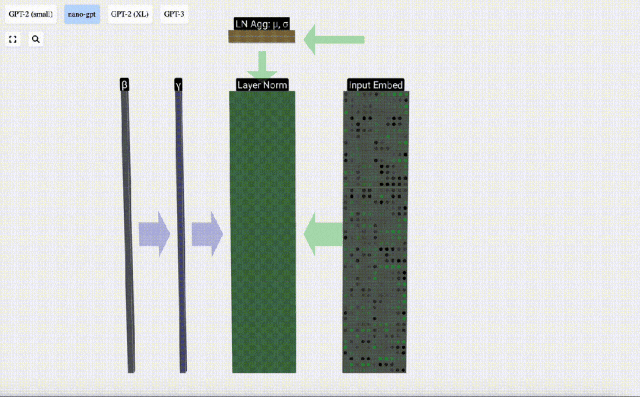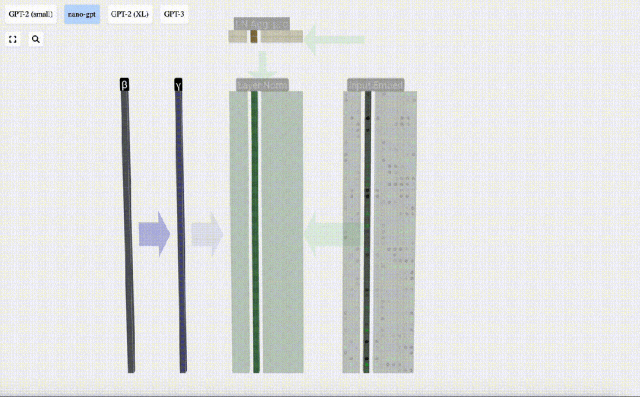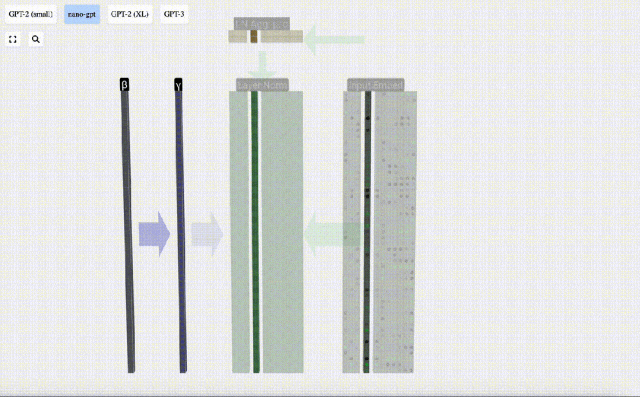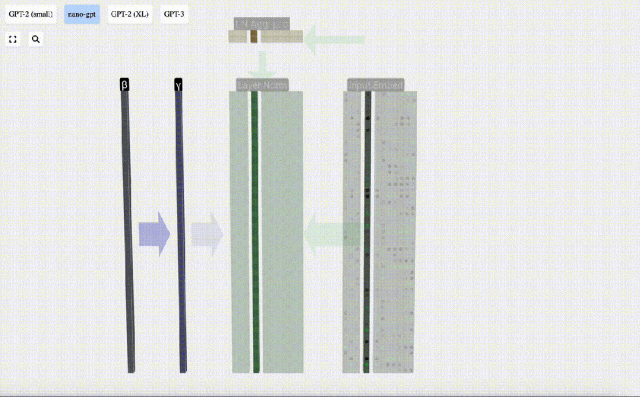
Matlamat normalisasi adalah untuk menjadikan nilai setiap lajur mempunyai min 0 dan sisihan piawai 1. Untuk mencapai ini, kirakan min dan sisihan piawai bagi setiap lajur, kemudian tolak min yang sepadan dan bahagikan dengan sisihan piawai yang sepadan untuk setiap lajur.
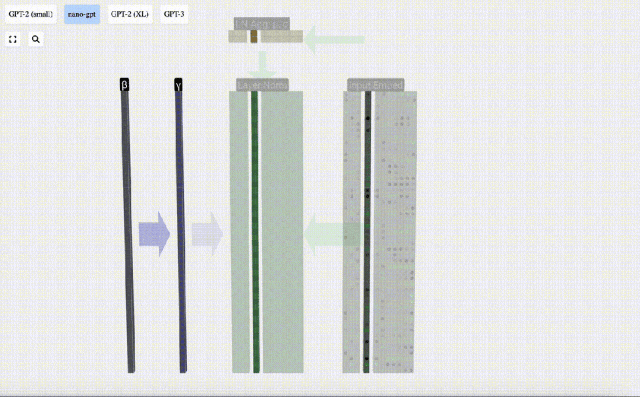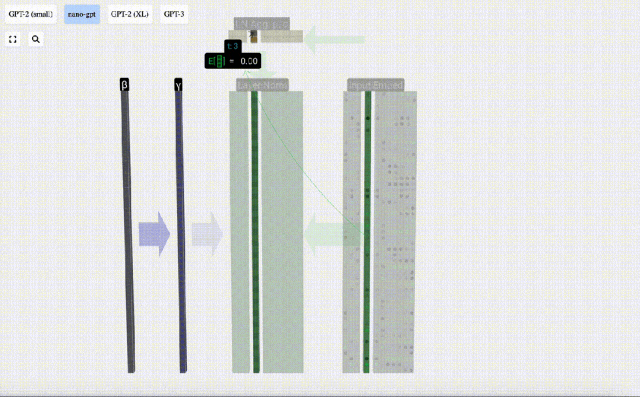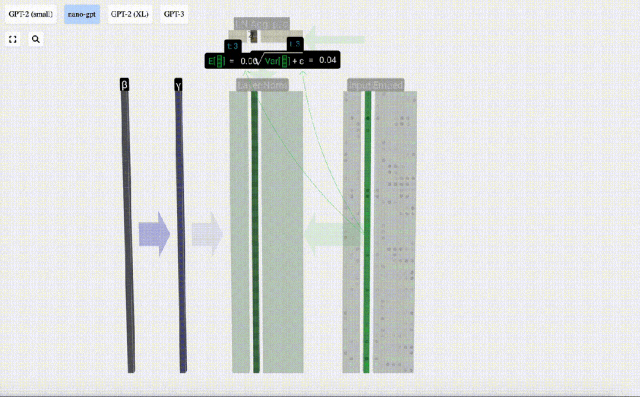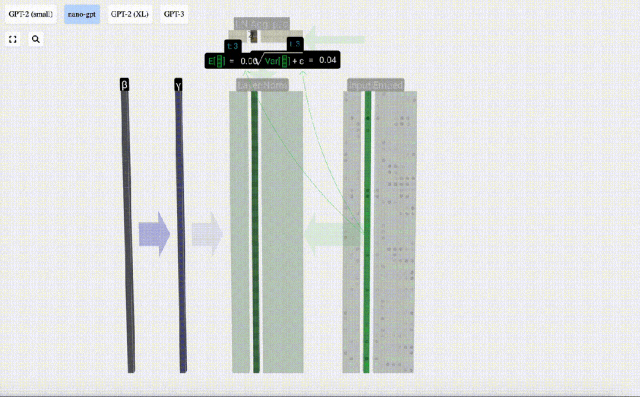
Di sini E[x] digunakan untuk mewakili min, dan Var[x] digunakan untuk mewakili varians (kuadrat sisihan piawai). epsilon(ε = 1×10^-5) adalah untuk mengelakkan pembahagian dengan ralat 0.
Kira dan simpan hasil ternormal, kemudian darabkannya dengan berat berat pembelajaran(γ) dan tambah bias bias(β) untuk mendapatkan hasil ternormal akhir.
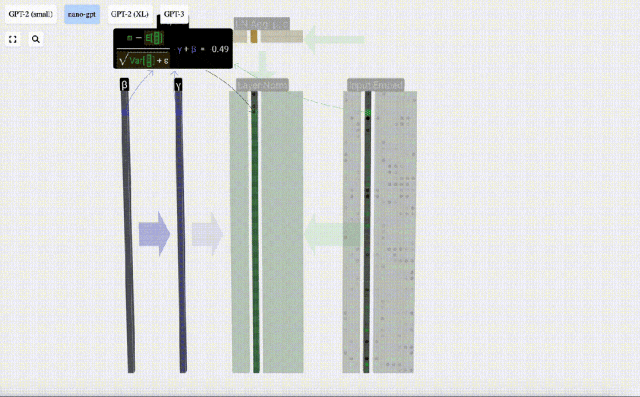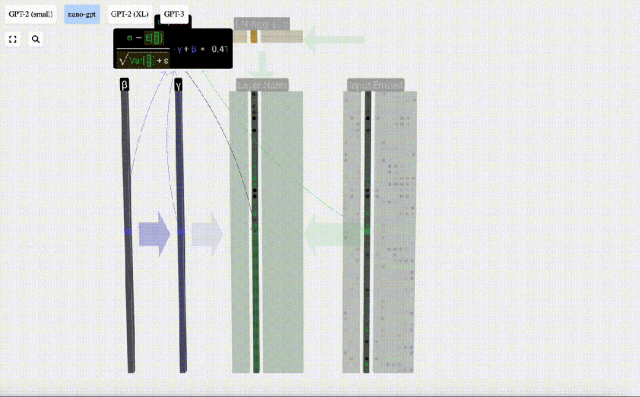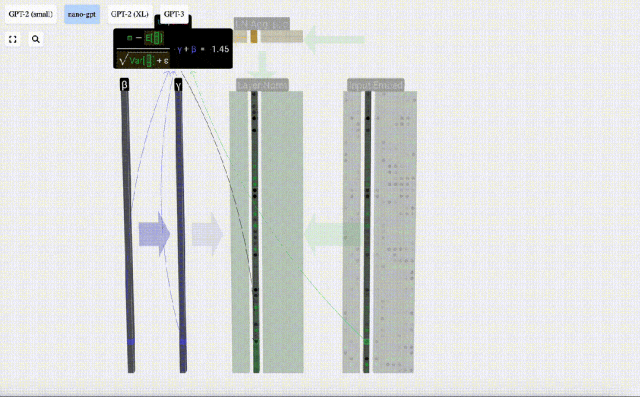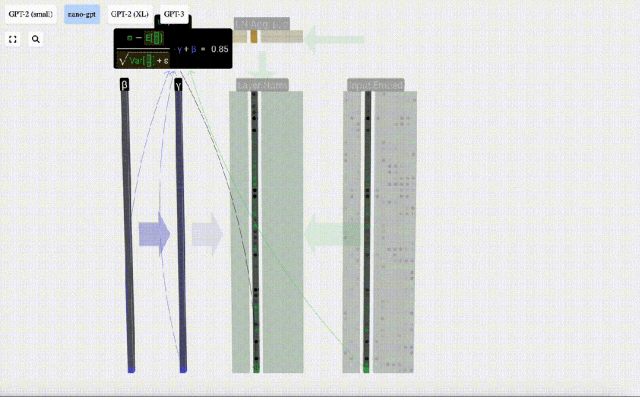
Akhir sekali, laksanakan operasi penormalan pada setiap lajur matriks benam input untuk mendapatkan pembenaman input ternormal dan hantar ke Lapisan perhatian kendiri (perhatian kendiri).
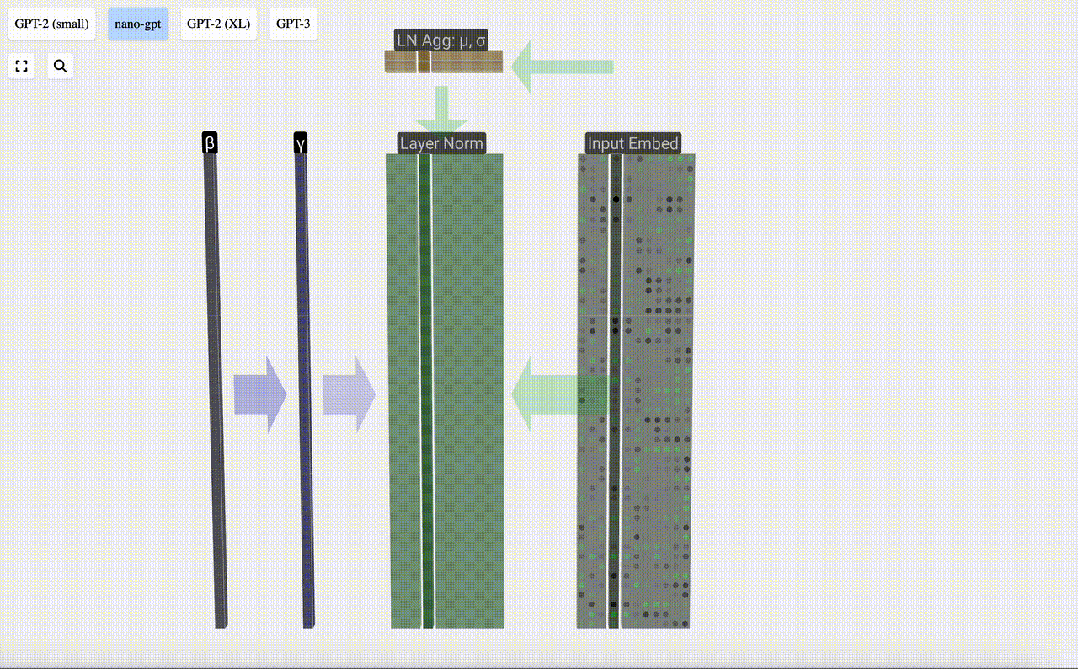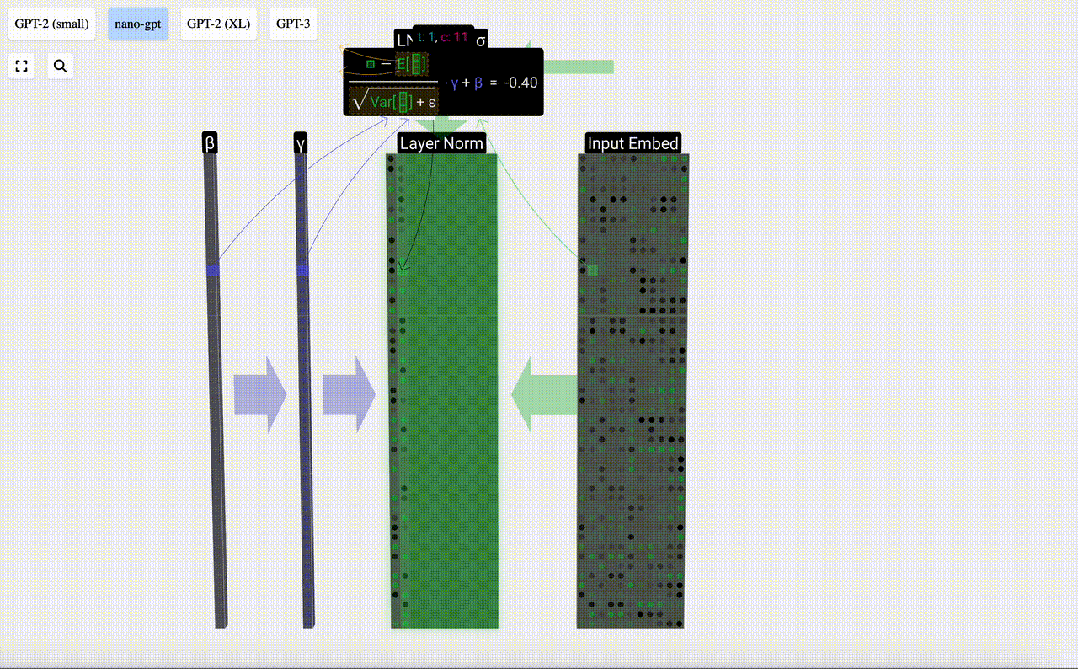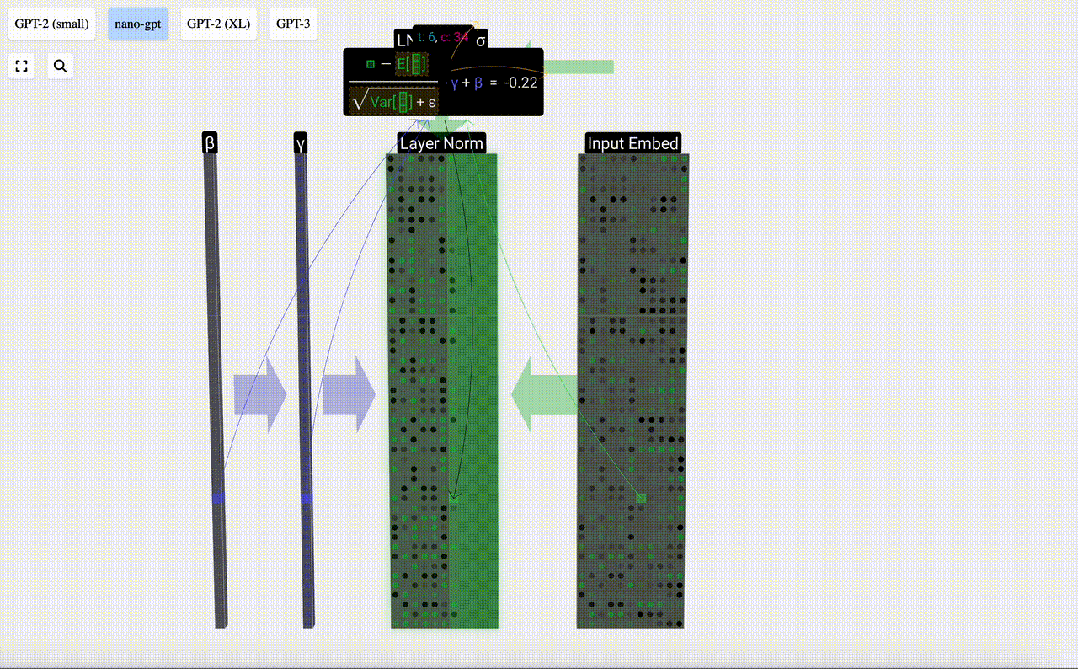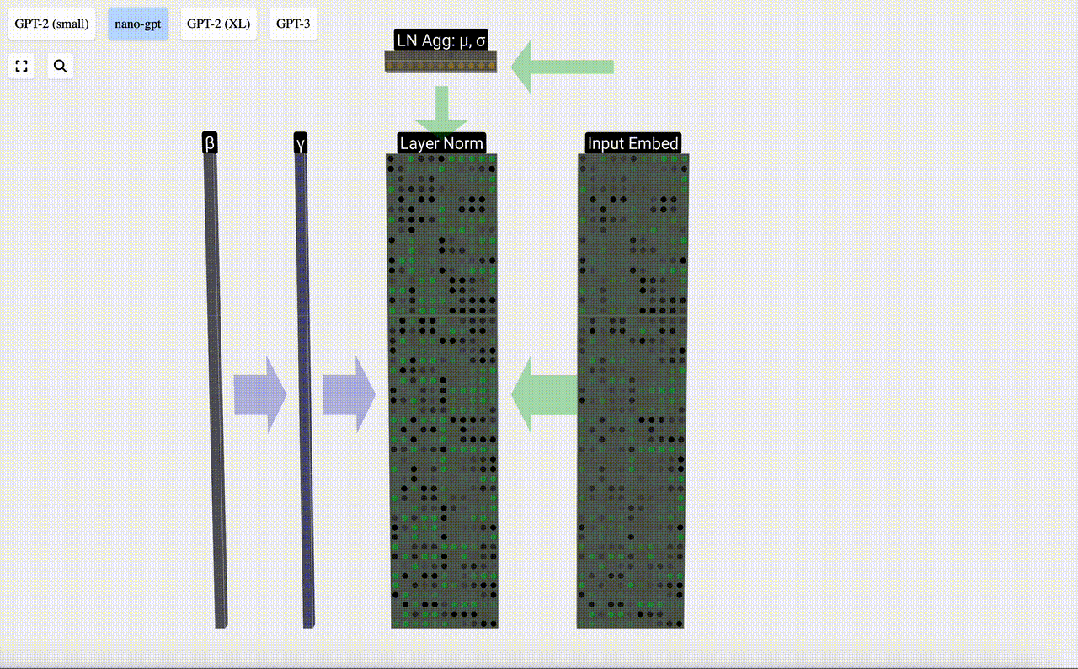
Perhatian Diri
Lapisan Perhatian Diri mungkin merupakan bahagian teras Transformer Pada peringkat ini, lajur dalam pembenaman input boleh "berkomunikasi" antara satu sama lain, manakala pada peringkat lain, setiap lajur wujud secara bebas.
Lapisan Perhatian Diri terdiri daripada pelbagai kepala perhatian diri Dalam contoh ini, terdapat tiga kepala perhatian diri. Input setiap pengepala ialah 1/3 daripada pembenaman input dan kami hanya memfokuskan pada salah satu daripadanya sekarang. . vektor Nilai vektor
 Untuk menjana vektor ini, pendaraban matriks-vektor digunakan, ditambah dengan bias. Setiap unit keluaran ialah gabungan linear vektor input.
Untuk menjana vektor ini, pendaraban matriks-vektor digunakan, ditambah dengan bias. Setiap unit keluaran ialah gabungan linear vektor input.
Sebagai contoh, untuk vektor pertanyaan, ia dilengkapkan dengan operasi produk titik antara baris matriks berat Q dan lajur matriks input.
- Pengendalian produk dot adalah sangat mudah, hanya darabkan elemen yang sepadan dan kemudian tambahkannya.
Ini adalah cara umum dan mudah untuk memastikan setiap elemen keluaran dipengaruhi oleh semua elemen dalam vektor input (pengaruh ini ditentukan oleh berat). Oleh itu, ia sering muncul dalam rangkaian saraf.
Dalam rangkaian neural, mekanisme ini sering berlaku kerana ia membolehkan model mengambil kira setiap bahagian jujukan input semasa memproses data. Mekanisme perhatian menyeluruh ini adalah teras kepada banyak seni bina rangkaian saraf moden, terutamanya apabila memproses data berjujukan seperti teks atau siri masa.
Kami mengulangi ini untuk setiap unit output dalam vektor Q, K, V: 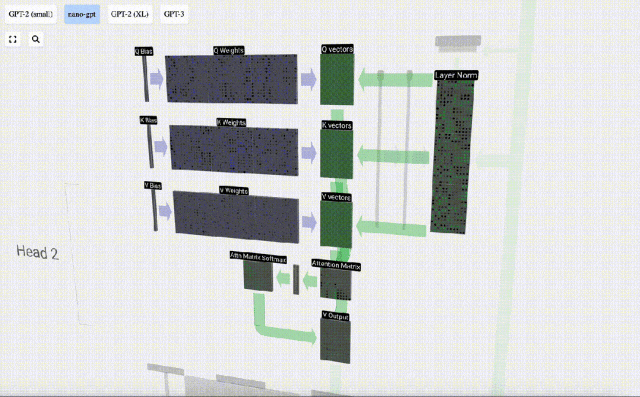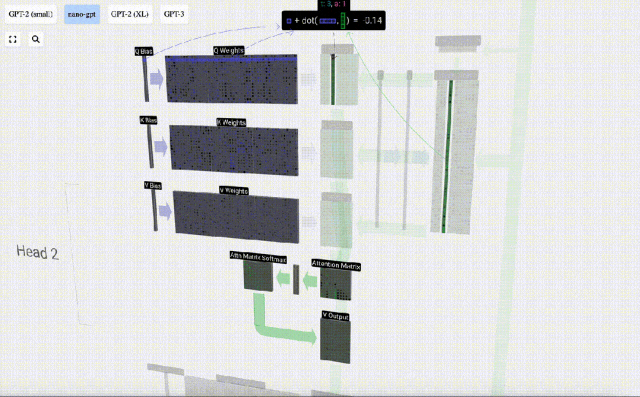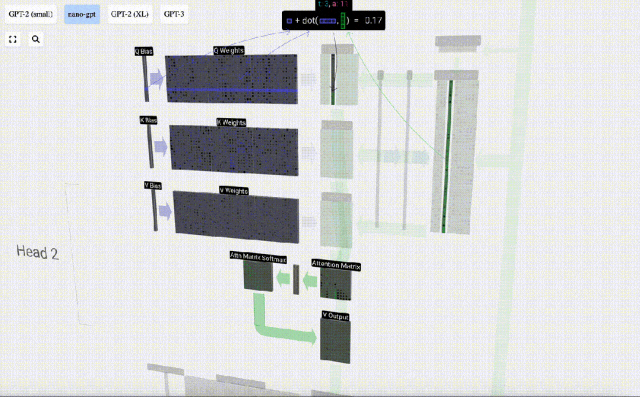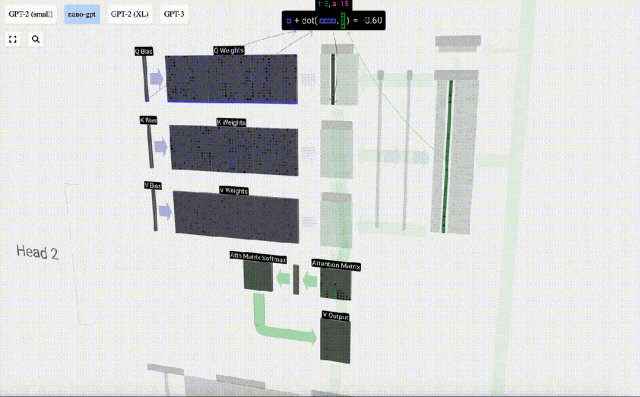
Bagaimanakah kita menggunakan vektor Q (pertanyaan), K (kunci) dan V (nilai) kami? Penamaan mereka memberi kita petunjuk: 'kunci' dan 'nilai' mengingatkan jenis kamus, dengan kunci dipetakan kepada nilai. Kemudian 'pertanyaan' ialah apa yang kita gunakan untuk mencari nilai. 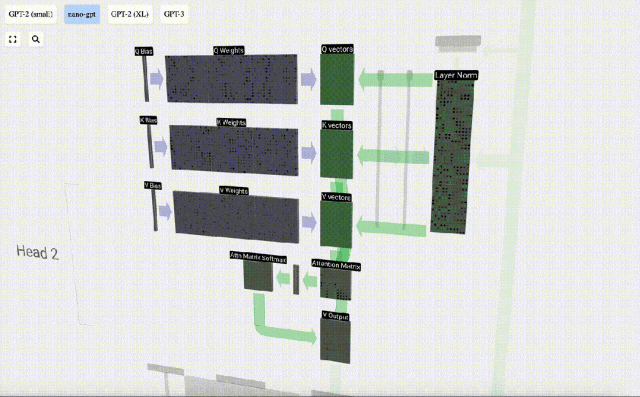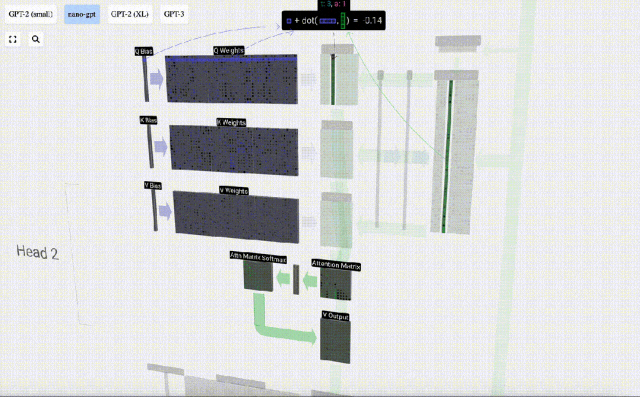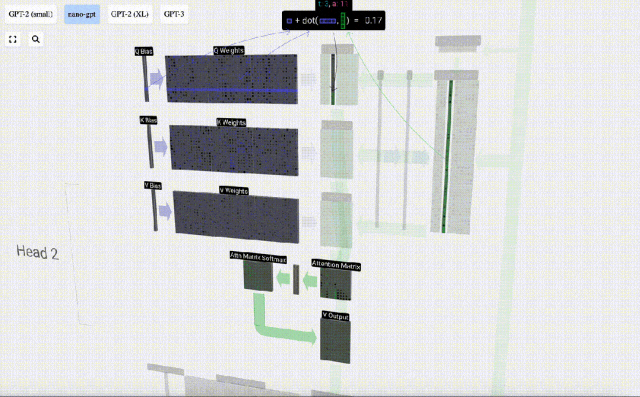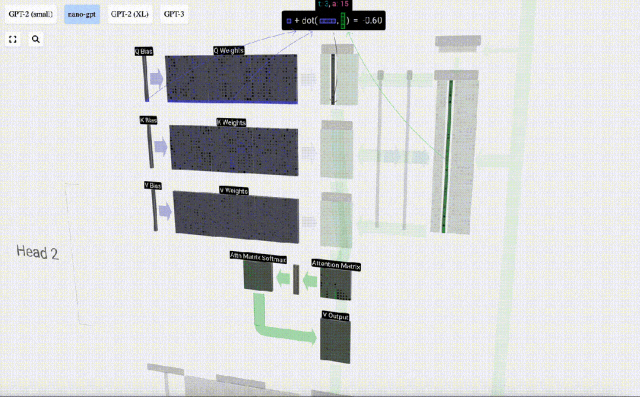
Dalam kes Perhatian Kendiri, bukannya mengembalikan satu vektor (istilah), kami mengembalikan beberapa gabungan berwajaran vektor (istilah). Untuk mencari pemberat ini, kami mengira hasil darab titik antara vektor Q dan setiap vektor K, timbang dan normalkan, dan akhirnya darabkannya dengan vektor V yang sepadan dan tambahkannya bersama.
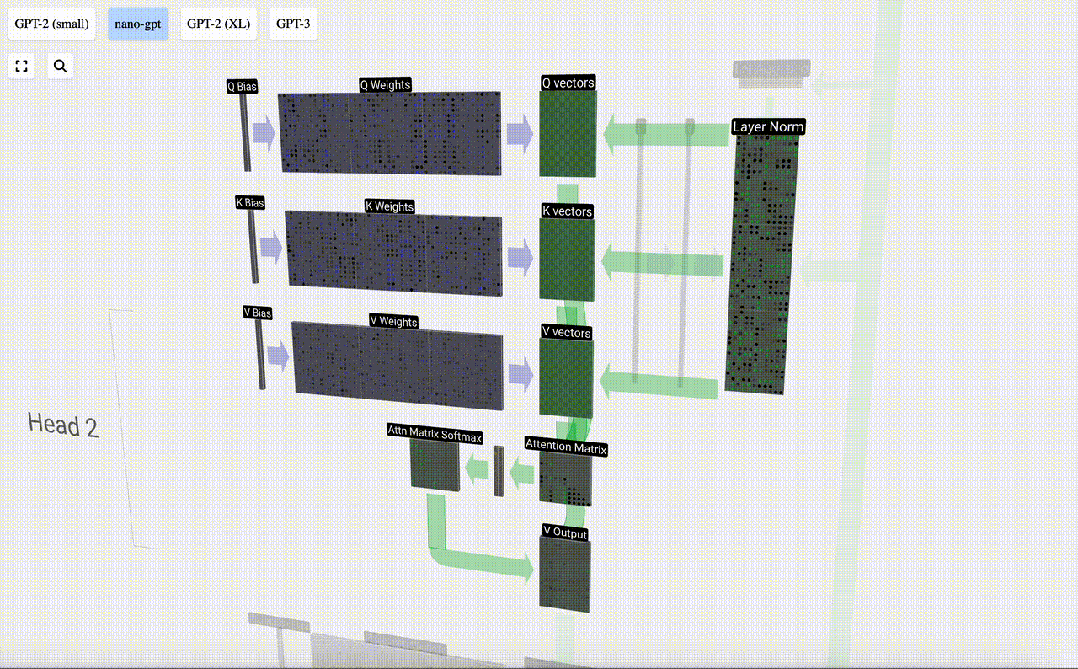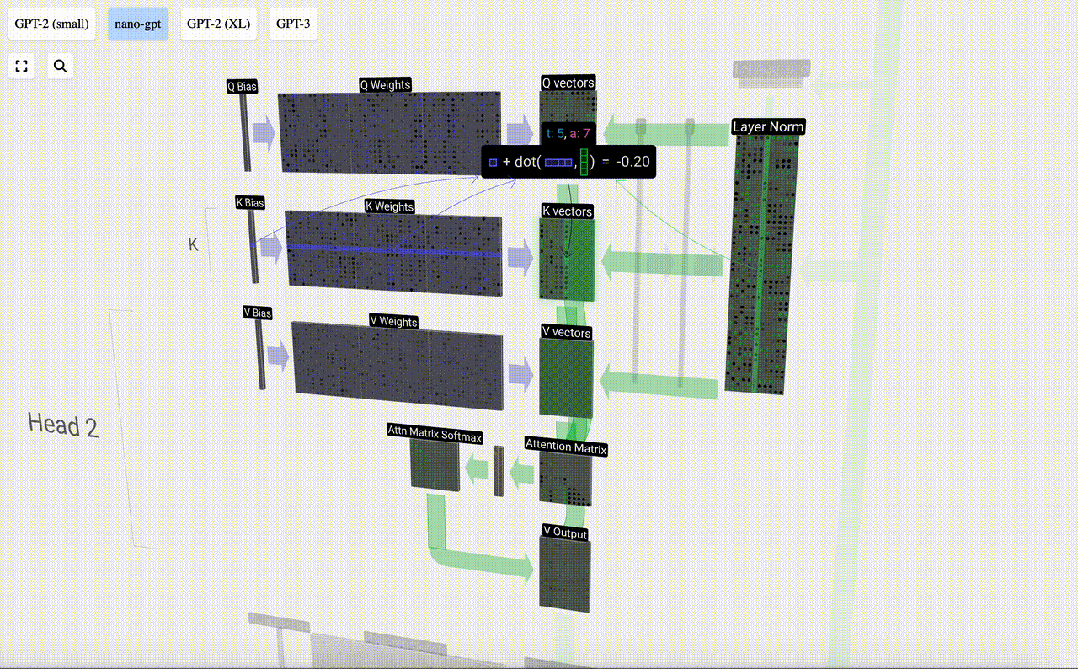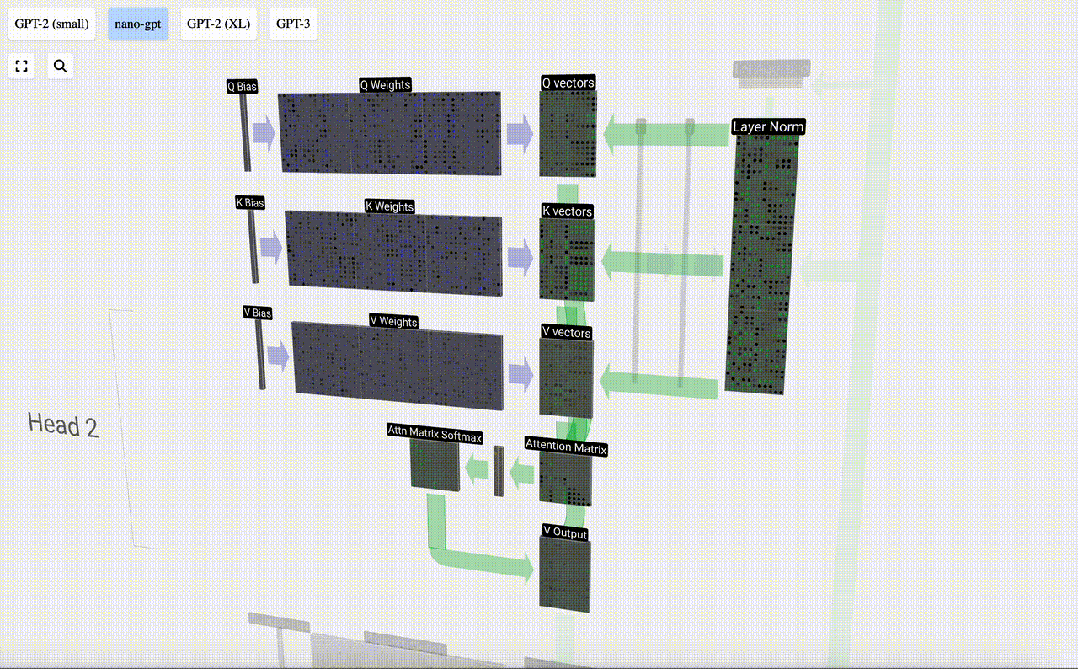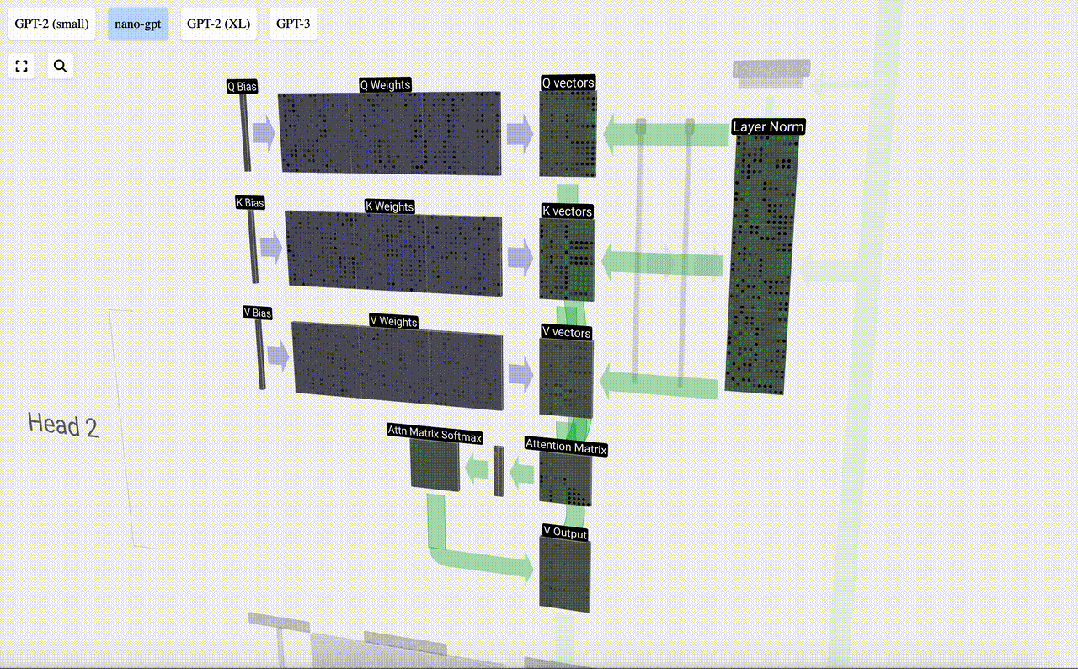 Mengambil lajur ke-6 sebagai contoh (t=5), pertanyaan akan bermula dari lajur ini:
Mengambil lajur ke-6 sebagai contoh (t=5), pertanyaan akan bermula dari lajur ini:
 Disebabkan kewujudan matriks perhatian, 6 lajur pertama KV boleh disoal, dan nilai Q ialah masa semasa.
Disebabkan kewujudan matriks perhatian, 6 lajur pertama KV boleh disoal, dan nilai Q ialah masa semasa.
Mula-mula hitung hasil darab titik antara vektor Q lajur semasa (t=5) dan vektor K lajur sebelumnya (6 lajur pertama). Ini kemudiannya disimpan dalam baris yang sepadan (t=5) matriks perhatian.

Saiz produk titik mengukur persamaan antara dua vektor Lebih besar produk titik, lebih serupa.
Dan hanya vektor Q yang dikendalikan dengan vektor K yang lalu, menjadikannya perhatian diri kausal. Dengan kata lain, token tidak boleh 'melihat maklumat masa depan'. 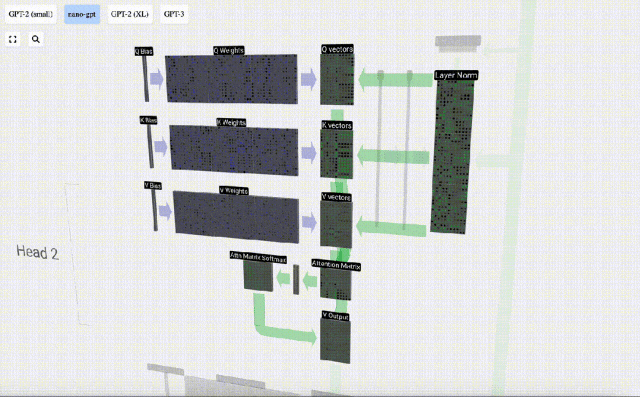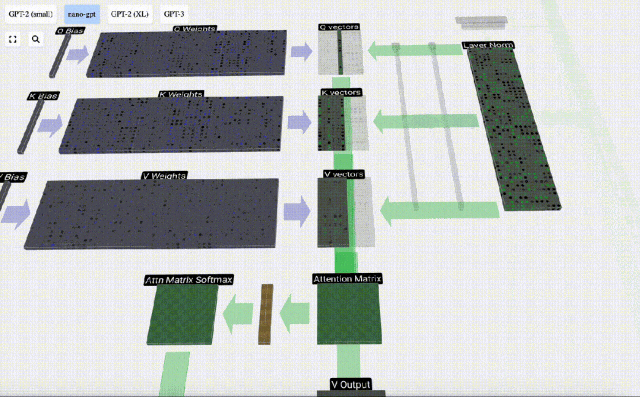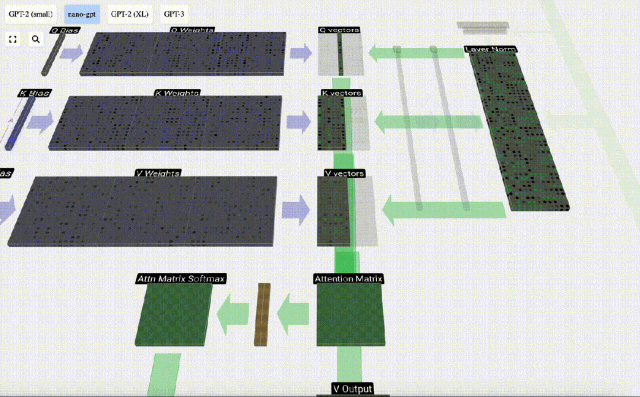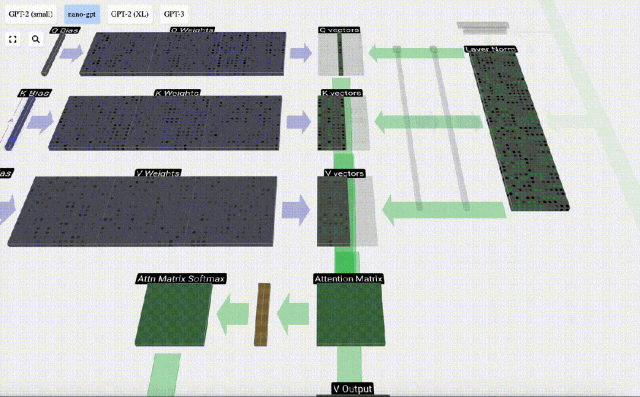
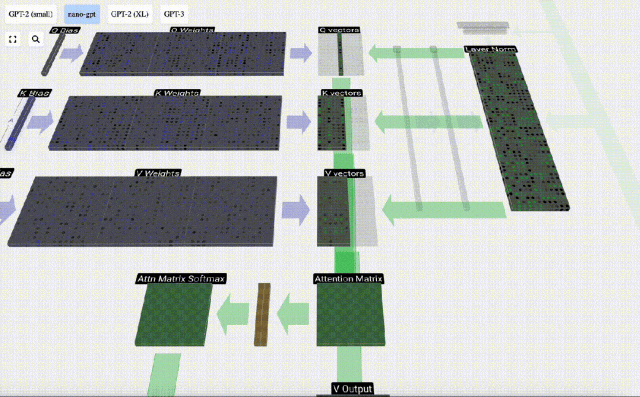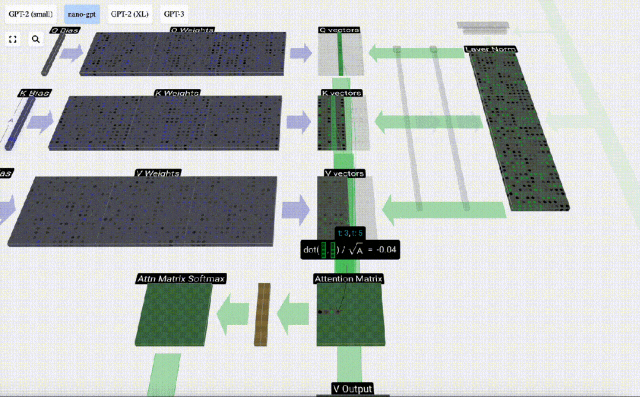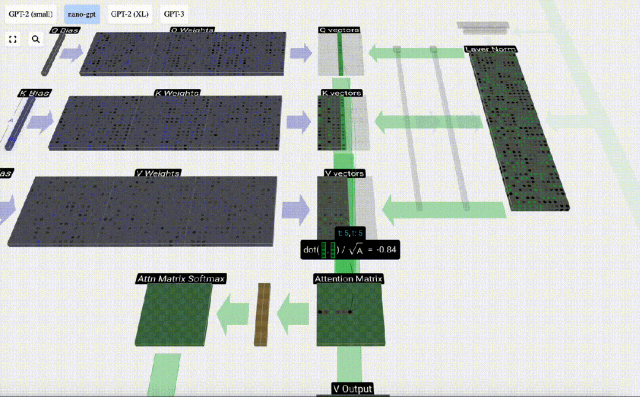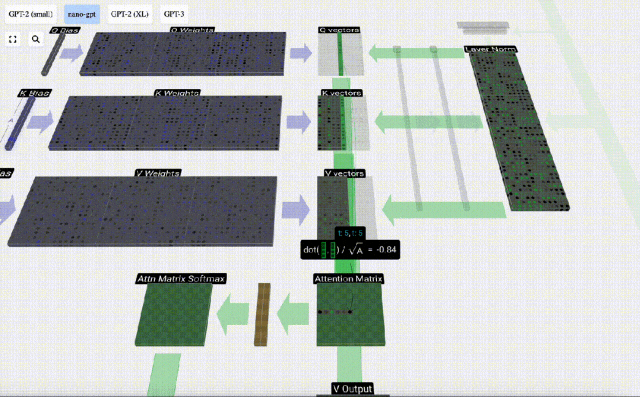
Kita kemudian boleh menambah vektor ini bersama-sama untuk mendapatkan vektor output. Oleh itu, vektor keluaran akan dikuasai oleh vektor V dengan resolusi tinggi.
Kini kami menerapkannya pada semua lajur.
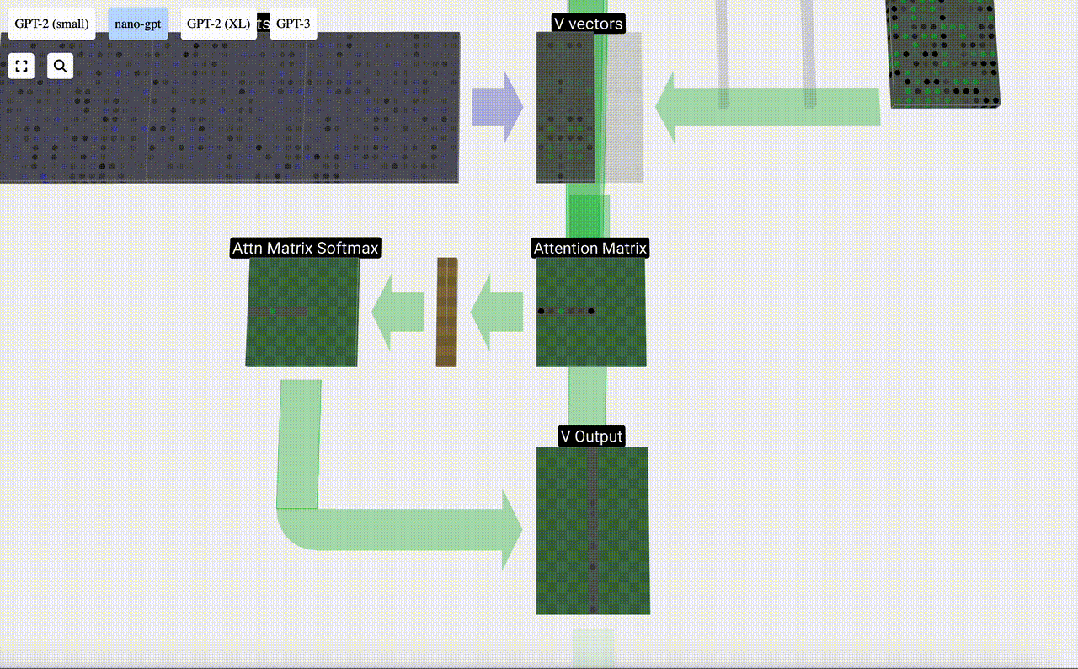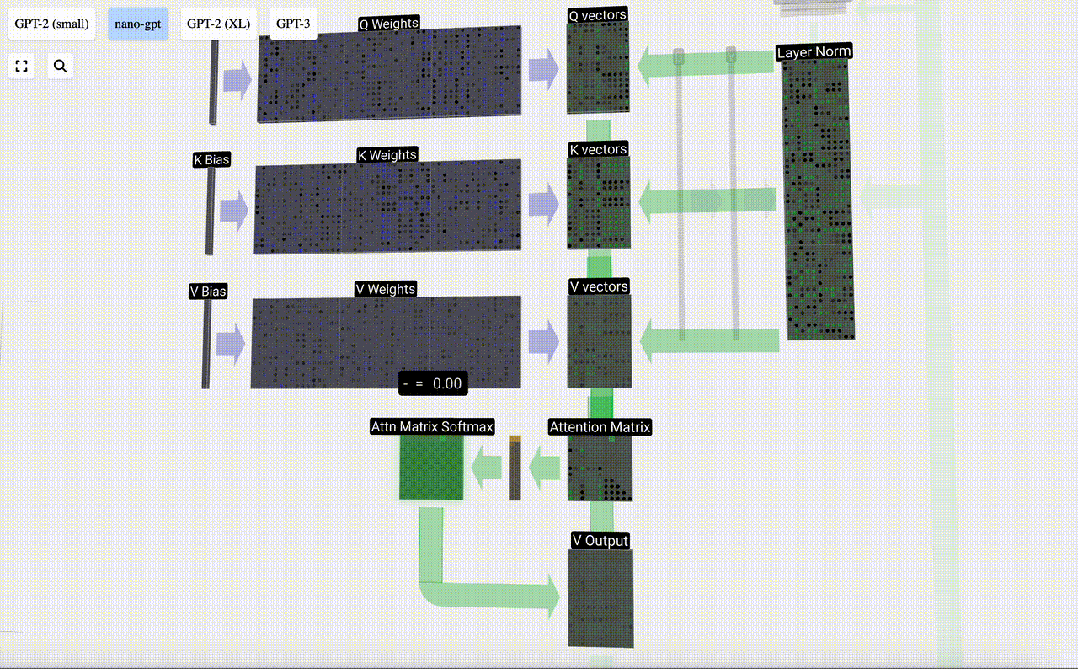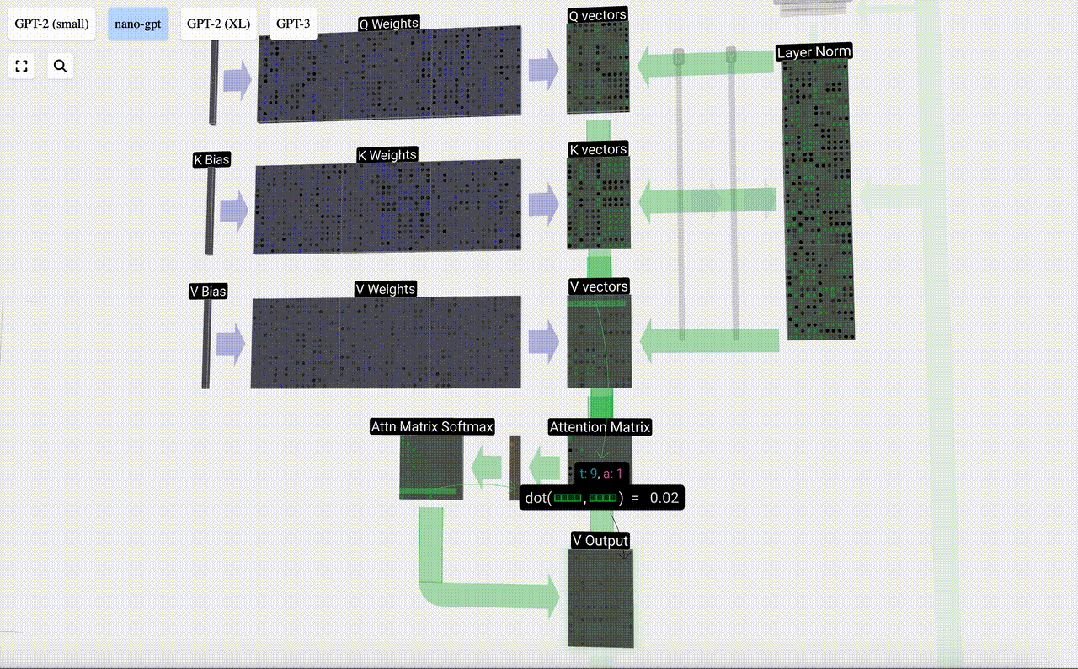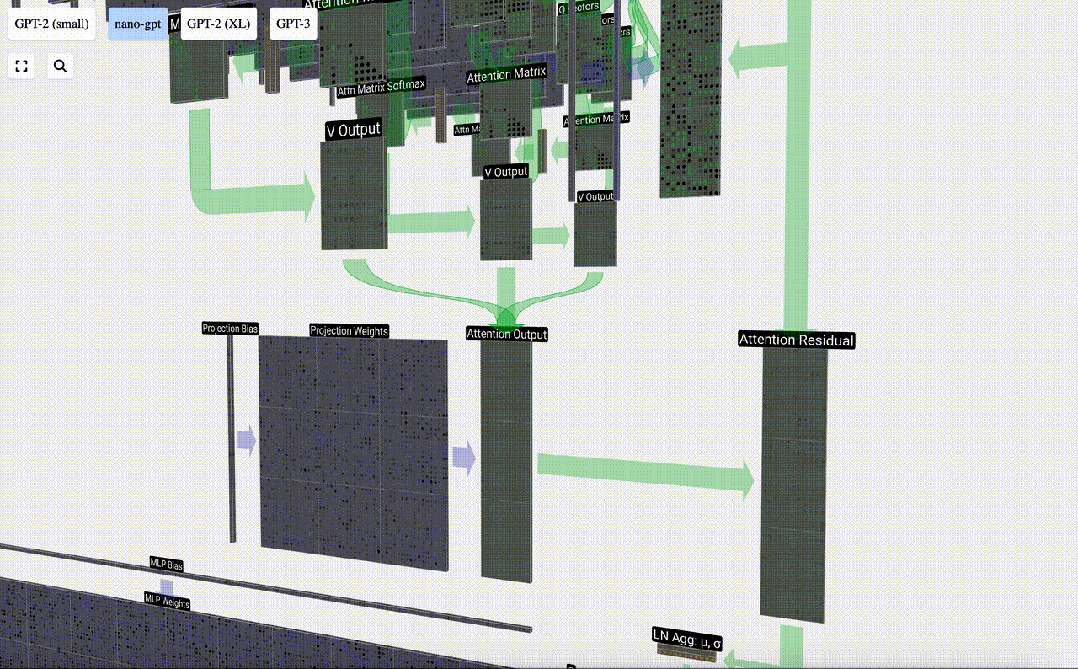
Ini adalah proses pemprosesan header dalam lapisan Self Attention. "Jadi matlamat utama Perhatian Sendiri ialah setiap lajur ingin mencari maklumat yang berkaitan daripada lajur lain dan mengekstrak nilainya, dan ia melakukan ini dengan membandingkan vektor Pertanyaannya dengan Kunci lajur lain tersebut. Had tambahan ialah ia hanya Boleh lihat ke arah masa lalu. Output ini adalah vektor V yang diadun dengan sewajarnya, dipengaruhi oleh vektor Q dan K. Untuk menggabungkan vektor output setiap kepala, kami hanya menyusunnya bersama-sama. Oleh itu, pada t=4, kita akan menokokkan 3 vektor dengan panjang A=16 untuk membentuk 1 vektor dengan panjang C=48.
Perlu diperhatikan bahawa dalam GPT, panjang vektor dalam kepala (A=16) adalah sama dengan C/num_heads. Ini memastikan bahawa apabila kita menyusunnya semula, kita mendapat panjang asal C.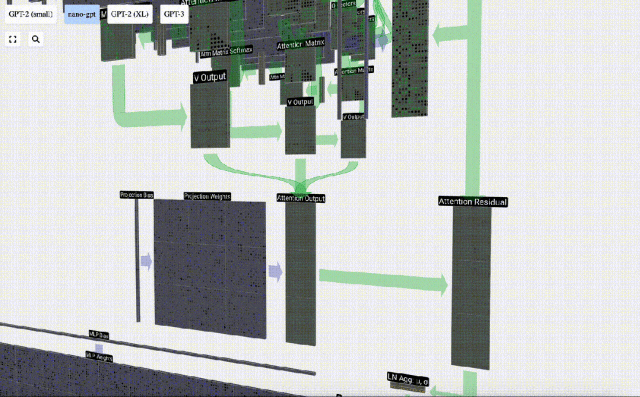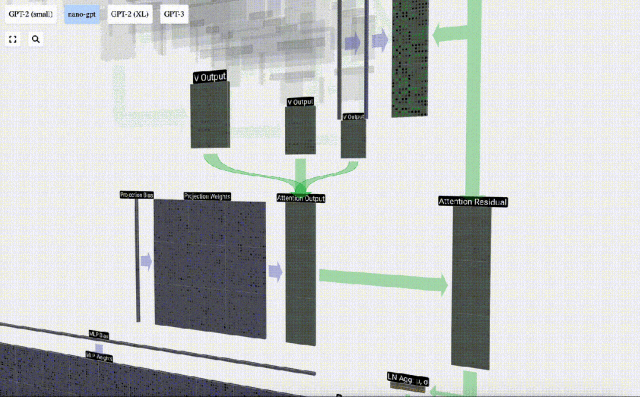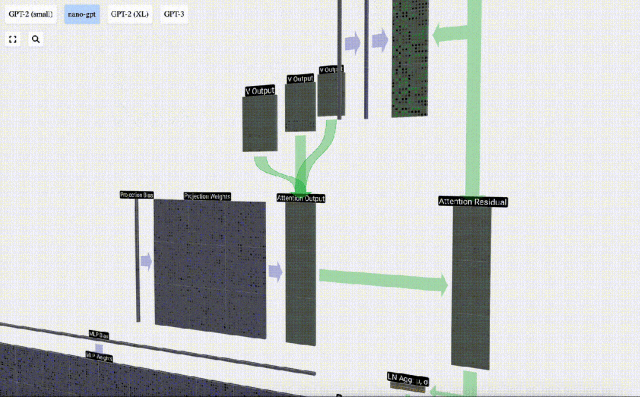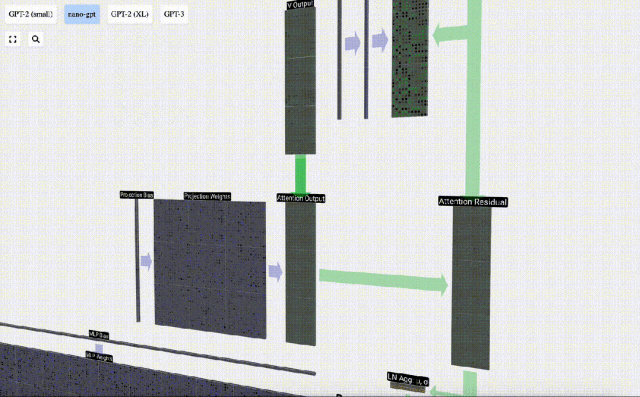 Berdasarkan ini, kami melakukan unjuran untuk mendapatkan output lapisan ini. Ini ialah pendaraban matriks-vektor mudah, setiap lajur, ditambah bias.
Berdasarkan ini, kami melakukan unjuran untuk mendapatkan output lapisan ini. Ini ialah pendaraban matriks-vektor mudah, setiap lajur, ditambah bias.
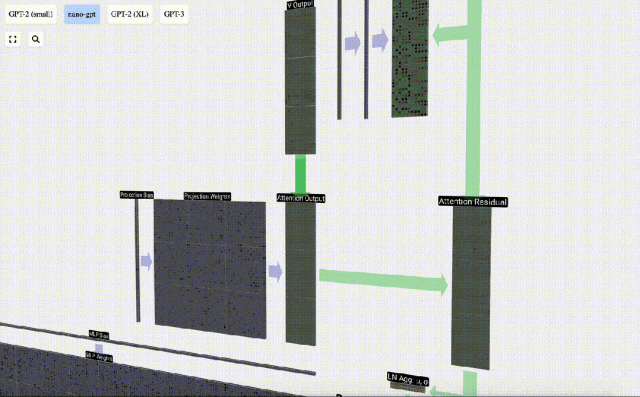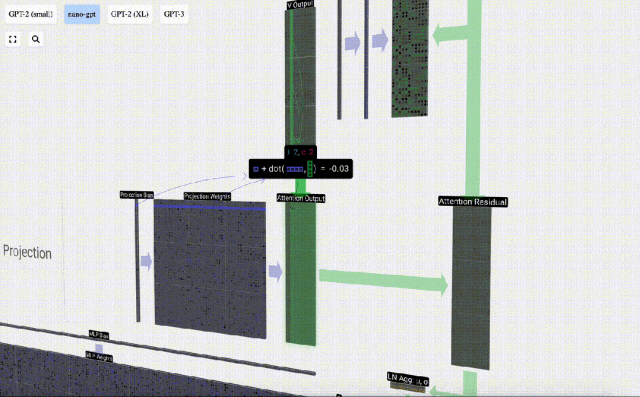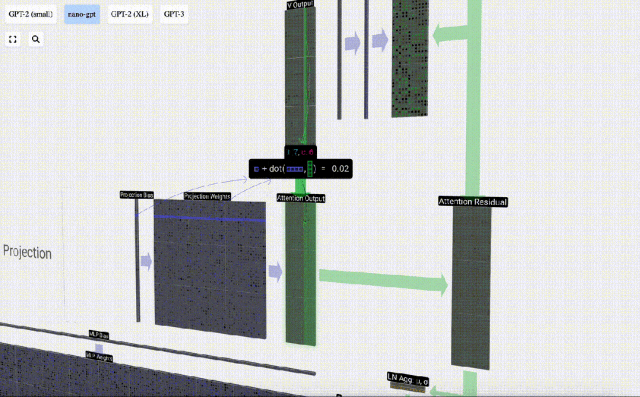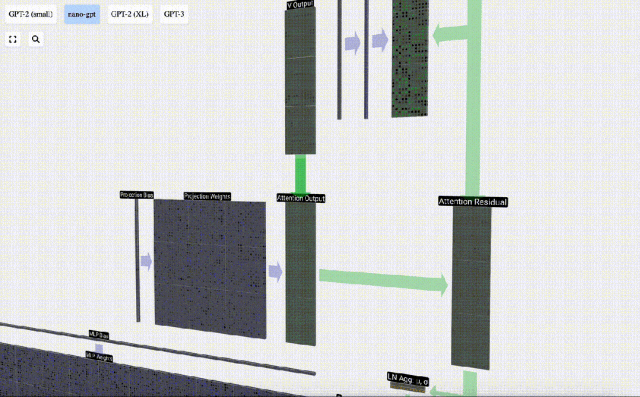 Daripada menghantar output ini terus ke peringkat seterusnya, kami menambahkannya sebagai elemen kepada pembenaman input. Proses ini, yang diwakili oleh anak panah menegak hijau, dipanggil sambungan baki atau laluan baki.
Daripada menghantar output ini terus ke peringkat seterusnya, kami menambahkannya sebagai elemen kepada pembenaman input. Proses ini, yang diwakili oleh anak panah menegak hijau, dipanggil sambungan baki atau laluan baki.
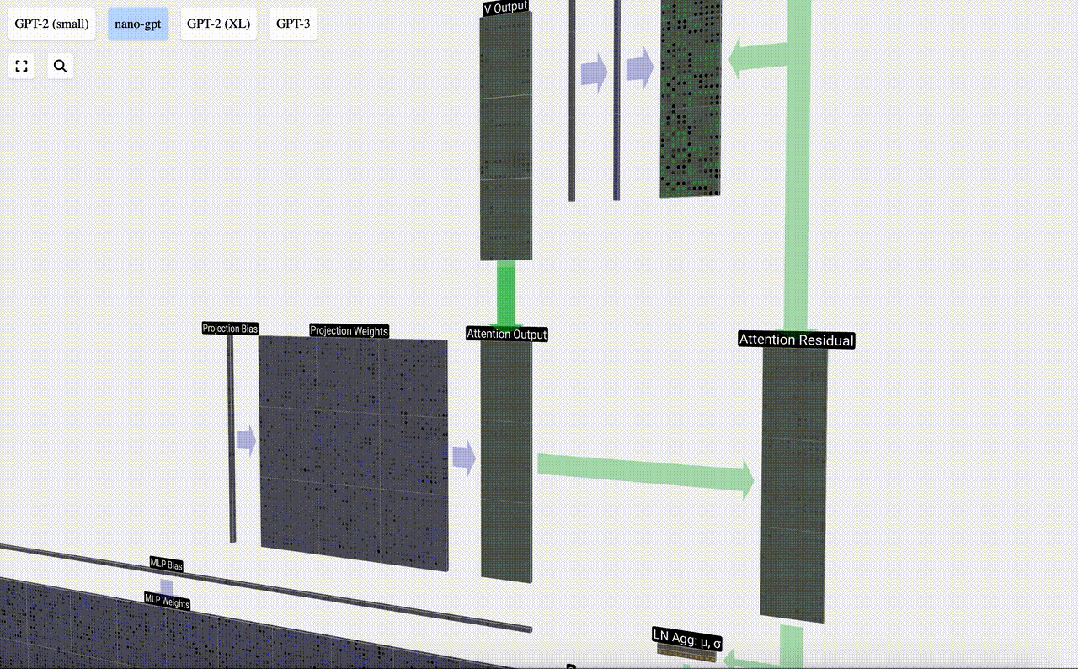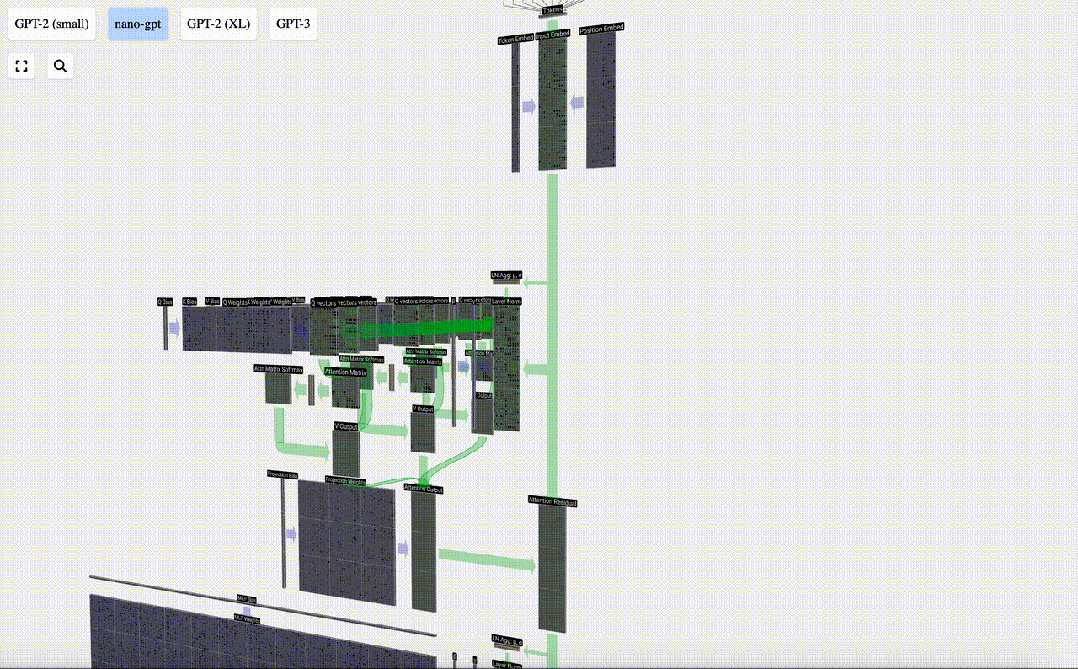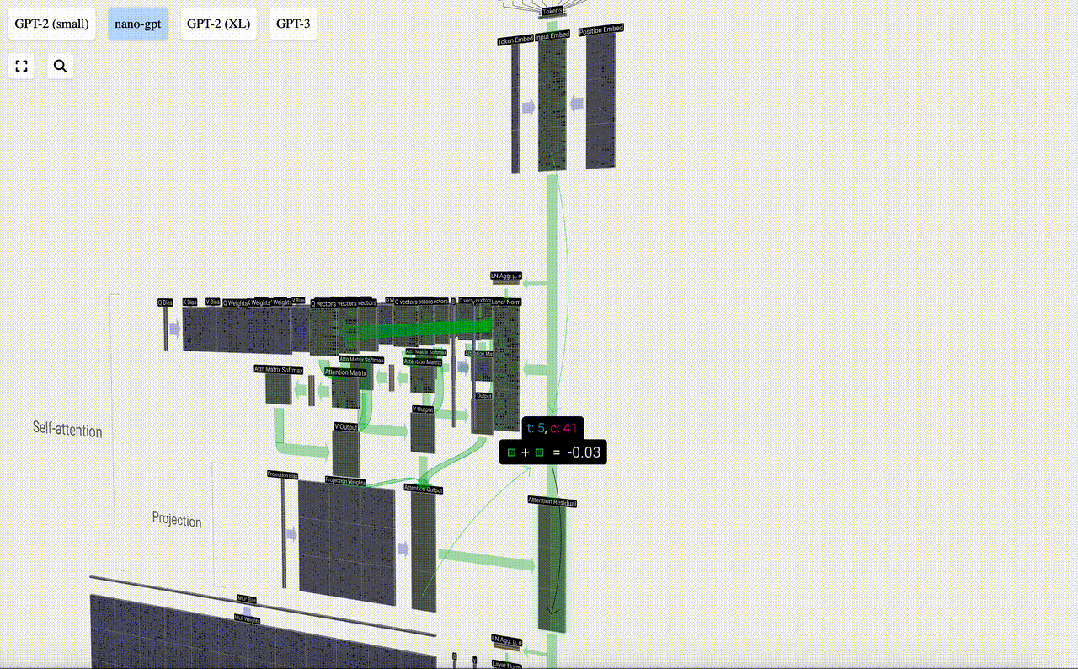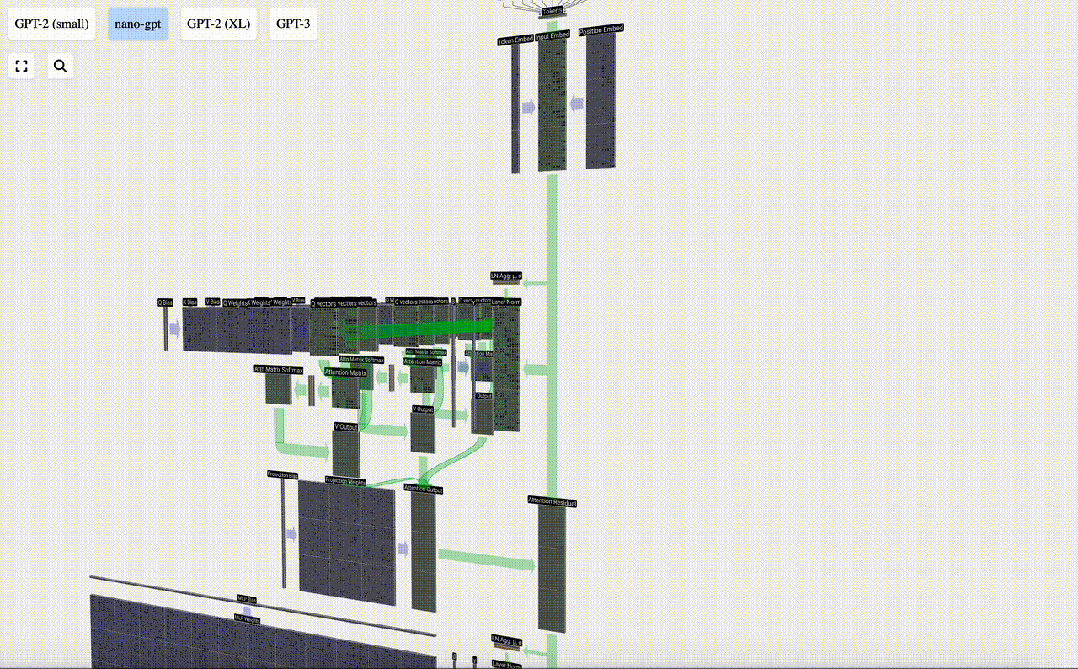 Sekarang kita mempunyai hasil daripada perhatian diri, kita boleh meneruskannya ke lapisan Transformer seterusnya: rangkaian suapan hadapan.
Sekarang kita mempunyai hasil daripada perhatian diri, kita boleh meneruskannya ke lapisan Transformer seterusnya: rangkaian suapan hadapan.
Multilayer Perceptron MLP
Selepas Perhatian Sendiri, bahagian seterusnya modul Transformer ialah MLP (Multilayer Perceptron), di sini ia adalah rangkaian neural ringkas dengan dua lapisan.
Sama seperti Perhatian Sendiri, sebelum vektor memasuki MLP, kita perlu melakukan normalisasi lapisan.
Pada masa yang sama, dalam MLP, pemprosesan berikut perlu dilakukan (secara bebas) untuk setiap vektor lajur panjang C=48:
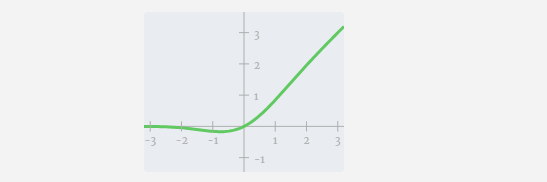
Tambahkan penjelmaan linear dengan pincang (iaitu, pendaraban matriks-vektor ditambah operasi pincang) , ditukar kepada vektor panjang 4 * C. Fungsi pengaktifan GELU (elemen yang diaplikasikan).- Lakukan penjelmaan linear dengan pincang, dan kemudian tukarkannya semula menjadi vektor panjang C.
- Mari kita kesan salah satu vektor:
 Mula-mula lakukan pendaraban matriks-vektor dan tambah offset untuk mengembangkan vektor menjadi matriks panjang 4*C. (Perhatikan bahawa matriks output di sini ditranspose untuk visualisasi)
Mula-mula lakukan pendaraban matriks-vektor dan tambah offset untuk mengembangkan vektor menjadi matriks panjang 4*C. (Perhatikan bahawa matriks output di sini ditranspose untuk visualisasi)
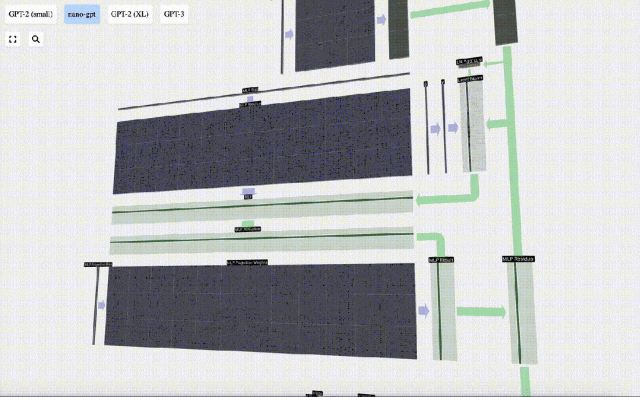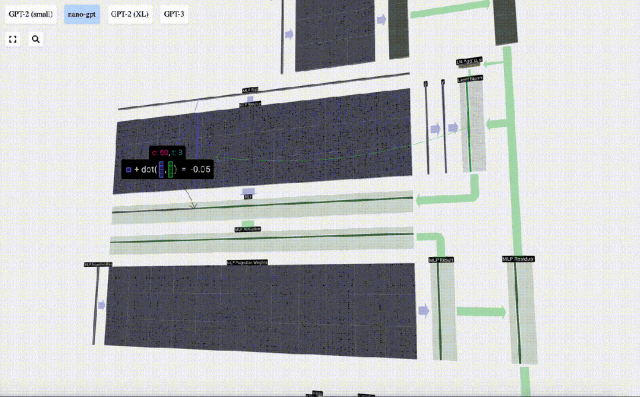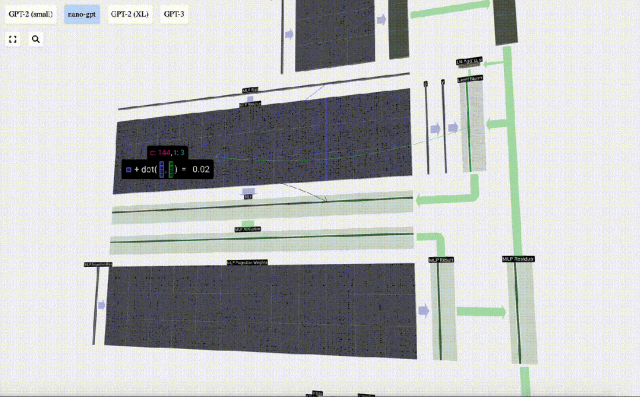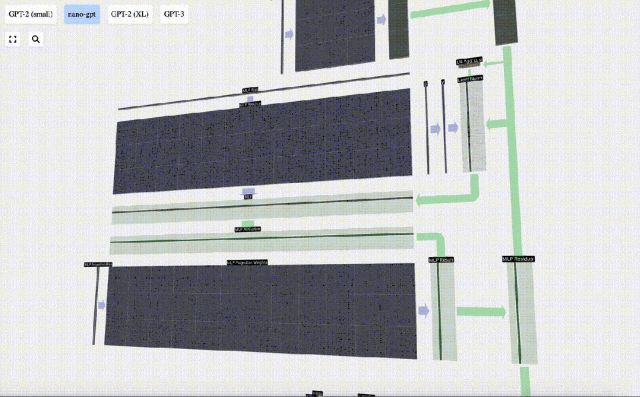
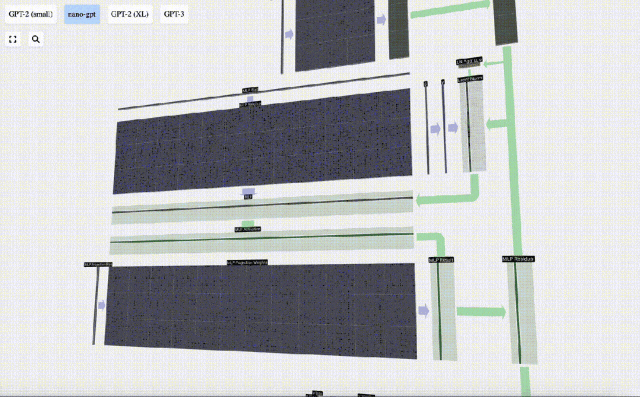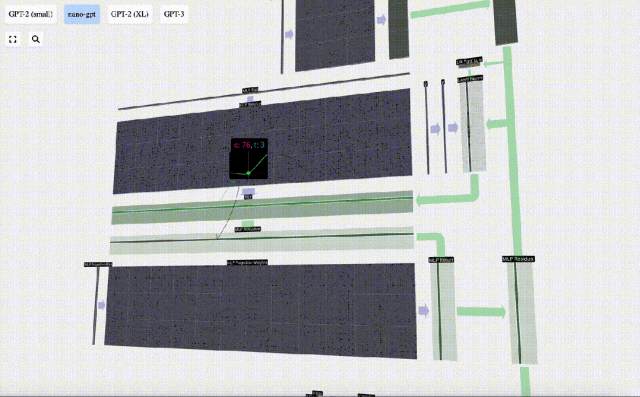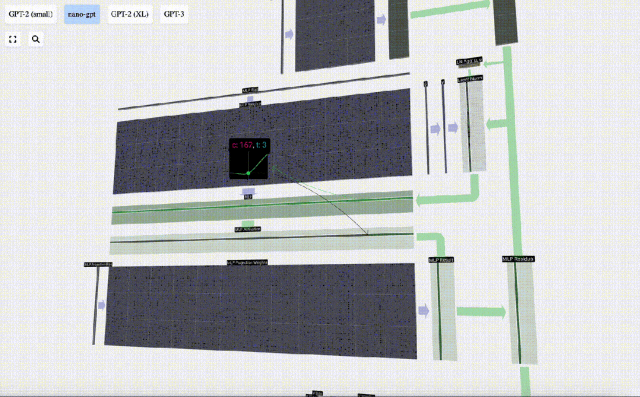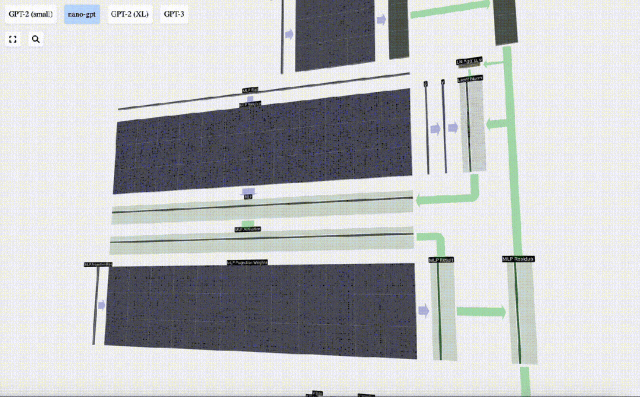
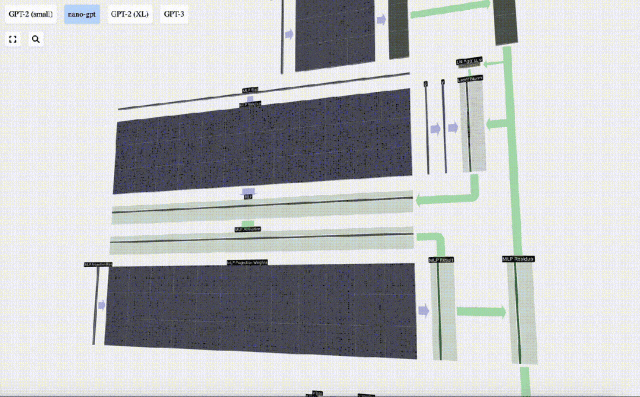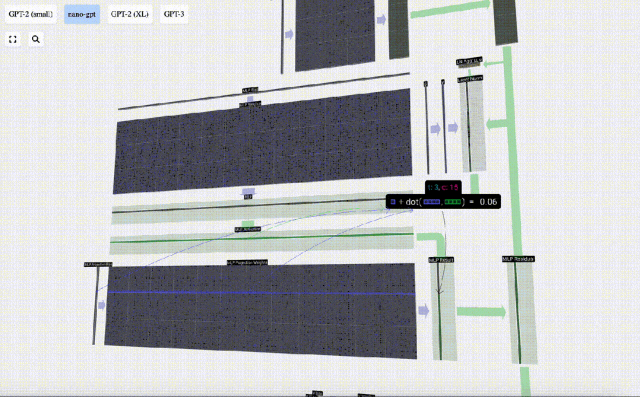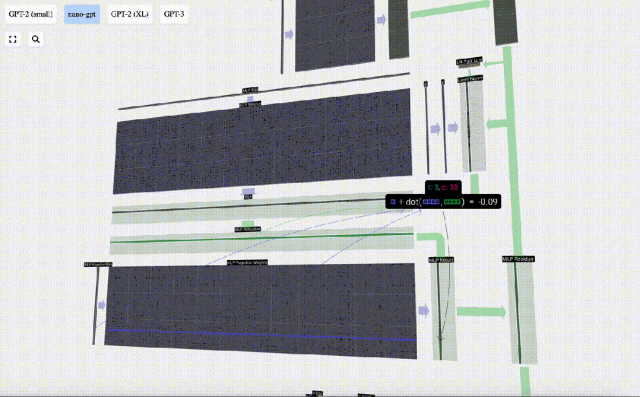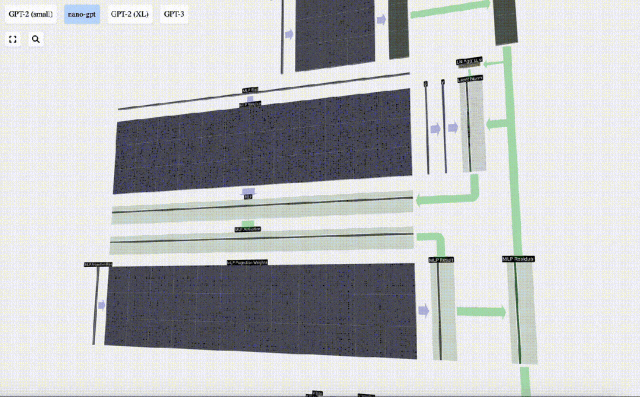
Ulang operasi ini.
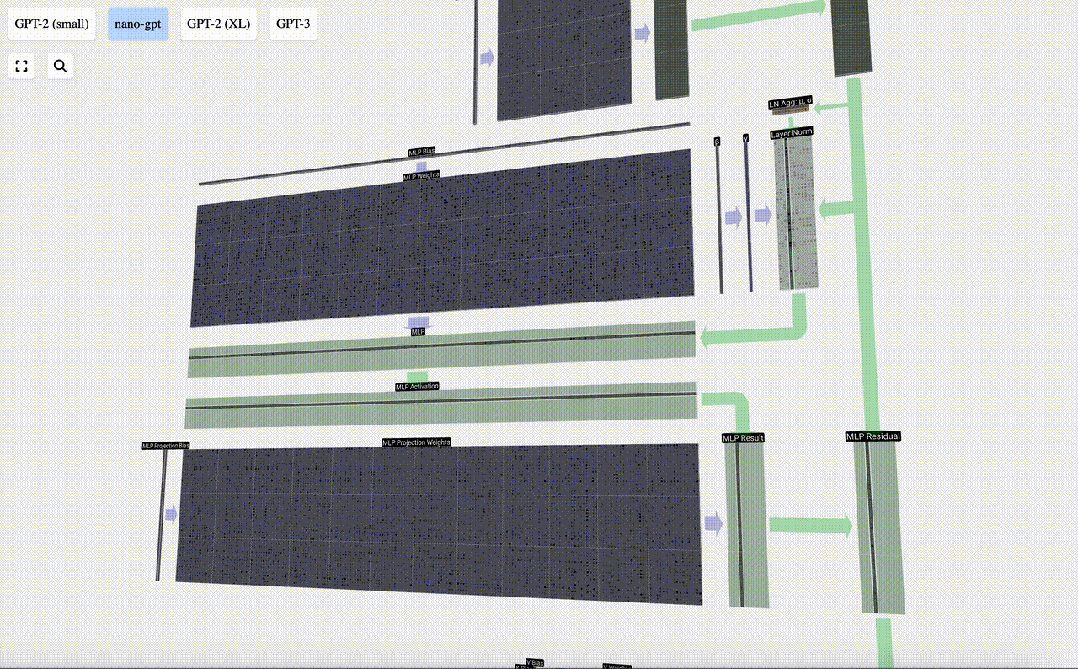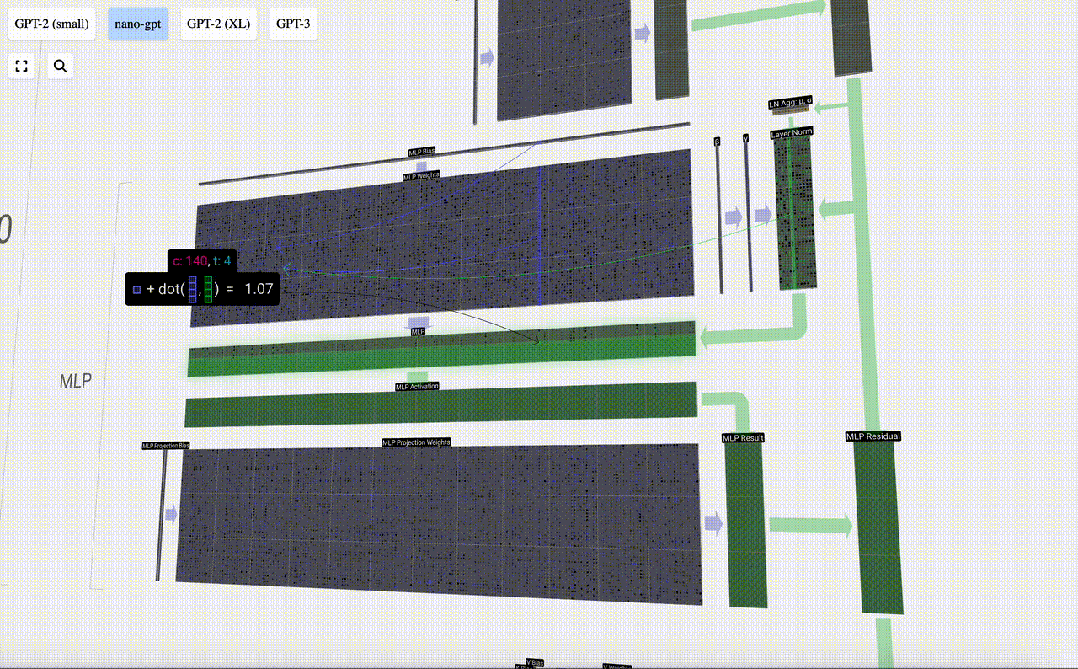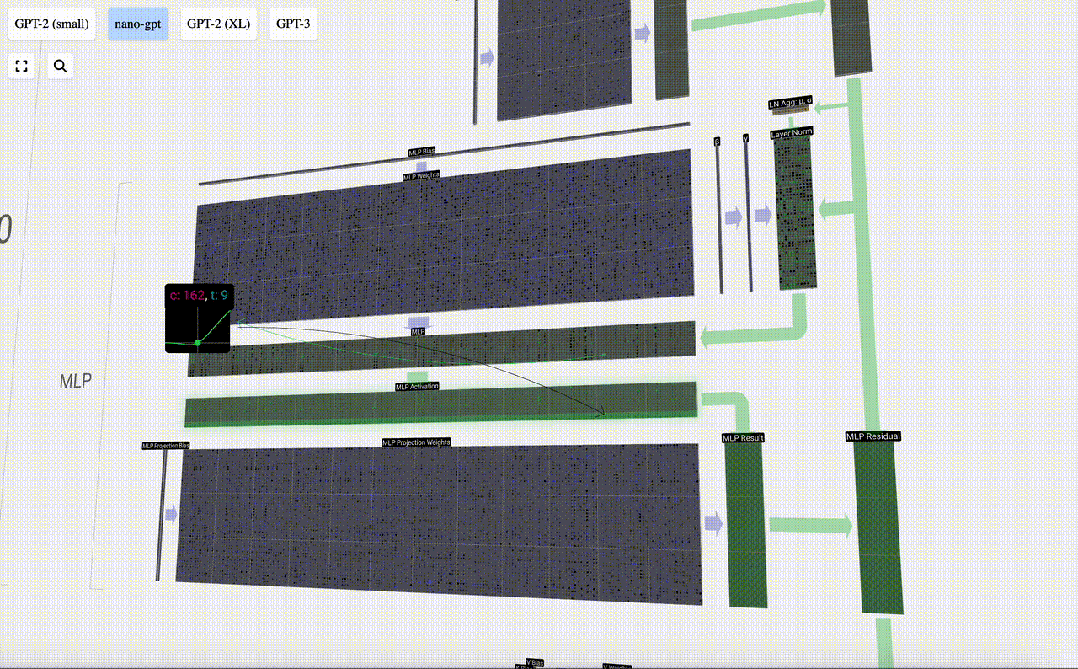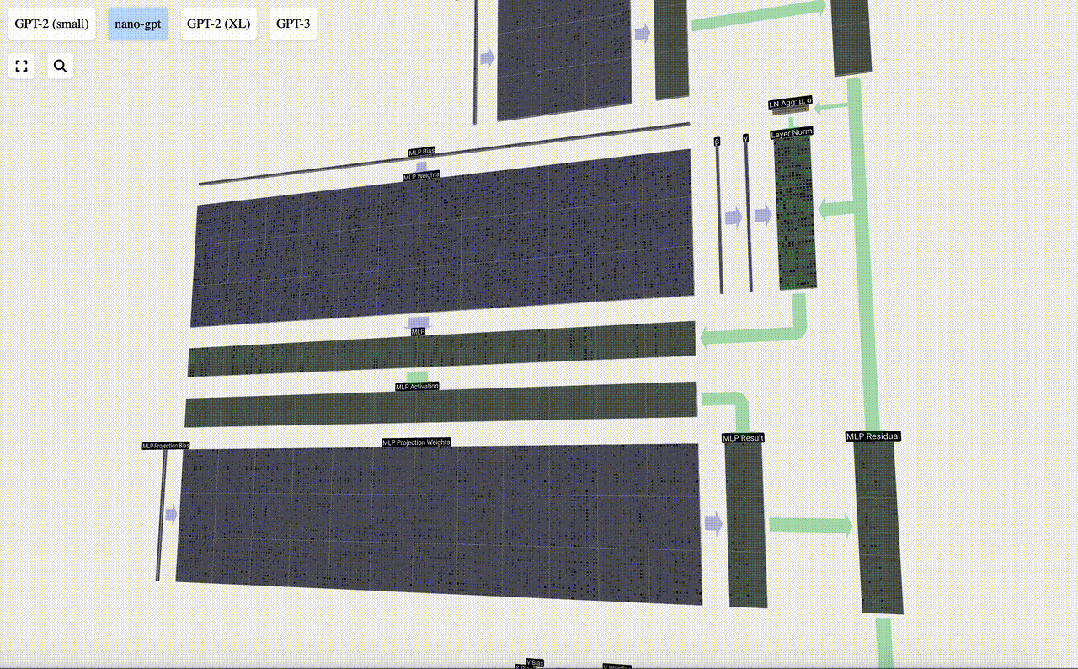
Ini adalah penghujung lapisan MLP, dan akhirnya kami mendapat output pengubah.
Transformer
Ini adalah modul Transformer yang lengkap!
Beberapa modul ini membentuk badan utama mana-mana model GPT, dan output setiap modul adalah input modul seterusnya.
Seperti biasa dalam pembelajaran mendalam, sukar untuk mengetahui dengan tepat apa yang dilakukan oleh setiap lapisan ini, tetapi kami mempunyai beberapa idea umum: lapisan awal cenderung untuk memfokuskan pada mempelajari ciri dan corak peringkat rendah, manakala lapisan kemudian Mengenali dan memahami lebih tinggi -abstraksi peringkat dan hubungan. Dalam konteks pemprosesan bahasa semula jadi, lapisan bawah mungkin mempelajari tatabahasa, sintaksis dan perkaitan leksikal yang mudah, manakala lapisan yang lebih tinggi mungkin menangkap hubungan semantik yang lebih kompleks, struktur wacana dan makna yang bergantung kepada konteks.
Softmax
Langkah terakhir ialah operasi softmax, yang mengeluarkan kebarangkalian ramalan bagi setiap token.
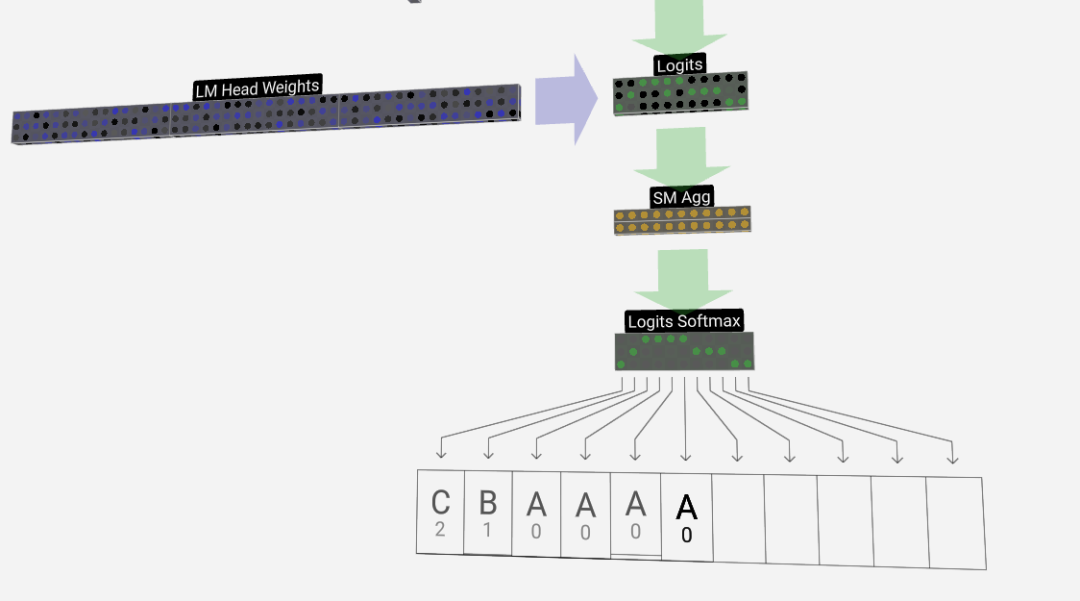
Output
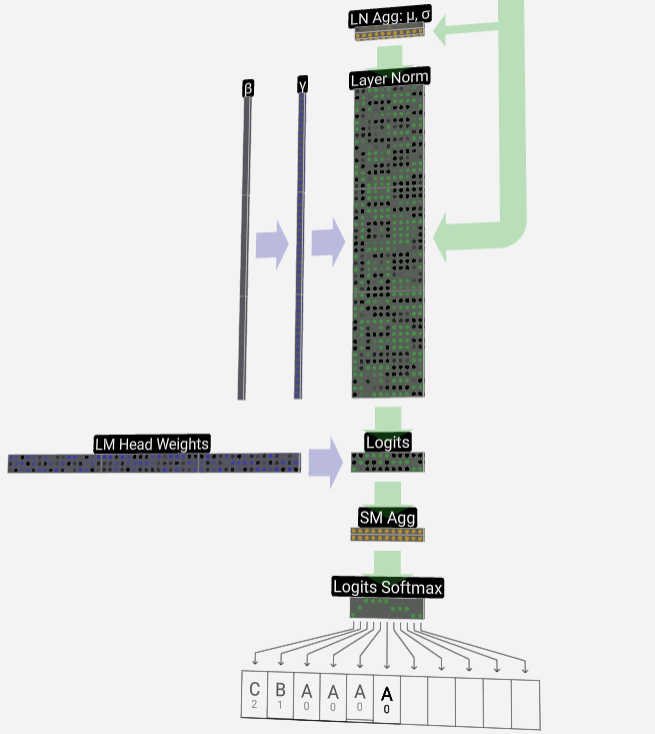
Akhirnya, kami sampai ke penghujung model. Keluaran Transformer terakhir mengalami lapisan regularisasi, diikuti dengan transformasi linear tidak berat sebelah.
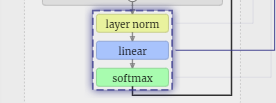
Transformasi terakhir ini menukarkan setiap vektor lajur kami daripada panjang C kepada nvocab panjang bersaiz perbendaharaan kata. Jadi ia sebenarnya menjana logit skor untuk setiap perkataan dalam perbendaharaan kata.
Untuk menukar skor ini kepada nilai kebarangkalian yang lebih intuitif, mereka perlu diproses melalui softmax terlebih dahulu. Jadi, untuk setiap lajur, kita mendapat kebarangkalian bahawa model diberikan kepada setiap perkataan dalam perbendaharaan kata.
Dalam model khusus ini, ia sebenarnya telah mempelajari semua jawapan tentang cara memesan tiga huruf, jadi kebarangkalian sangat condong ke arah jawapan yang betul.
Apabila kita membiarkan model maju dari semasa ke semasa, kita perlu menggunakan kebarangkalian lajur terakhir untuk memutuskan token tambahan seterusnya dalam jujukan. Sebagai contoh, jika kita memasukkan enam token ke dalam model, kita akan menggunakan kebarangkalian output dalam lajur enam.
Keluaran lajur ini ialah satu siri nilai kebarangkalian, dan kita sebenarnya perlu memilih salah satu daripadanya sebagai token seterusnya dalam jujukan. Kami mencapai ini dengan "pensampelan daripada pengedaran", iaitu, memilih token secara rawak berdasarkan kebarangkaliannya. Sebagai contoh, token dengan kebarangkalian 0.9 mempunyai kebarangkalian 90% untuk dipilih. Walau bagaimanapun, kami juga mempunyai pilihan lain, seperti sentiasa memilih token dengan kebarangkalian tertinggi.
Kita juga boleh mengawal "kelancaran" pengedaran dengan menggunakan parameter suhu. Suhu yang lebih tinggi akan menjadikan pengedaran lebih sekata, manakala suhu yang lebih rendah akan menjadikannya lebih tertumpu pada token dengan kebarangkalian tertinggi.
Kami melaraskan logit (output transformasi linear) dengan menggunakan parameter suhu sebelum menggunakan softmax, kerana eksponen dalam softmax mempunyai kesan penguatan yang ketara pada nilai yang lebih besar, dan menjadikan semua nilai lebih dekat akan mengurangkan kesan ini.
 Gambar
Gambar
Atas ialah kandungan terperinci Tembusi halangan maklumat! Alat visualisasi 3D berskala besar yang mengejutkan dikeluarkan!. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

