Rumah >Peranti teknologi >AI >Melaksanakan Model Pakar Campuran (MoE) menggunakan PyTorch
Melaksanakan Model Pakar Campuran (MoE) menggunakan PyTorch
- 王林ke hadapan
- 2024-01-16 08:42:16640semak imbas
Pelancaran Mixtral 8x7B telah menarik perhatian meluas dalam bidang AI terbuka, terutamanya konsep Mixture-of-Experts (KPM), yang terkenal kepada semua orang. Konsep Kepakaran Hibrid (KPM) melambangkan kecerdasan kolaboratif dan merangkumi idea bahawa keseluruhannya lebih besar daripada jumlah bahagiannya. Model MoE menyepadukan kelebihan pelbagai model pakar untuk memberikan ramalan yang lebih tepat. Ia terdiri daripada rangkaian berpagar dan satu set rangkaian pakar, setiap rangkaian pakar pandai mengendalikan aspek yang berbeza bagi tugas tertentu. Dengan memperuntukkan tugas dan pemberat dengan betul, model KPM boleh memanfaatkan kepakaran pakar, dengan itu meningkatkan prestasi ramalan keseluruhan. Model pintar kolaboratif ini telah membawa penemuan baharu kepada pembangunan bidang AI dan akan memainkan peranan penting dalam aplikasi masa hadapan.
Artikel ini akan menggunakan PyTorch untuk melaksanakan model MoE. Sebelum memperkenalkan kod khusus, mari kita perkenalkan secara ringkas seni bina pakar hibrid.
Seni Bina KPM
KPM terdiri daripada dua jenis rangkaian: (1) rangkaian pakar dan (2) rangkaian berpagar.
Rangkaian Pakar ialah kaedah yang menggunakan model proprietari yang berprestasi baik pada subset data. Konsep terasnya adalah untuk menampung ruang masalah melalui pelbagai pakar dengan kekuatan yang saling melengkapi untuk memastikan penyelesaian yang komprehensif kepada masalah tersebut. Setiap model pakar dilatih dengan keupayaan dan pengalaman unik, dengan itu meningkatkan prestasi dan keberkesanan sistem keseluruhan. Melalui penggunaan rangkaian pakar, tugas dan keperluan yang kompleks dapat ditangani dengan berkesan dan penyelesaian yang lebih baik disediakan.
Rangkaian berpagar ialah rangkaian yang digunakan untuk mengarah, menyelaras atau mengurus sumbangan pakar. Ia menentukan rangkaian mana yang terbaik untuk memproses input tertentu dengan mempelajari dan menimbang keupayaan rangkaian yang berbeza untuk jenis input yang berbeza. Rangkaian gating yang terlatih boleh menilai vektor input baharu dan menetapkan tugas pemprosesan kepada pakar atau gabungan pakar yang paling sesuai berdasarkan kecekapan mereka. Rangkaian gating melaraskan pemberat secara dinamik berdasarkan perkaitan output pakar dengan input semasa untuk memastikan respons yang diperibadikan. Mekanisme pelarasan berat secara dinamik ini membolehkan rangkaian gating menyesuaikan diri secara fleksibel kepada situasi dan keperluan yang berbeza.
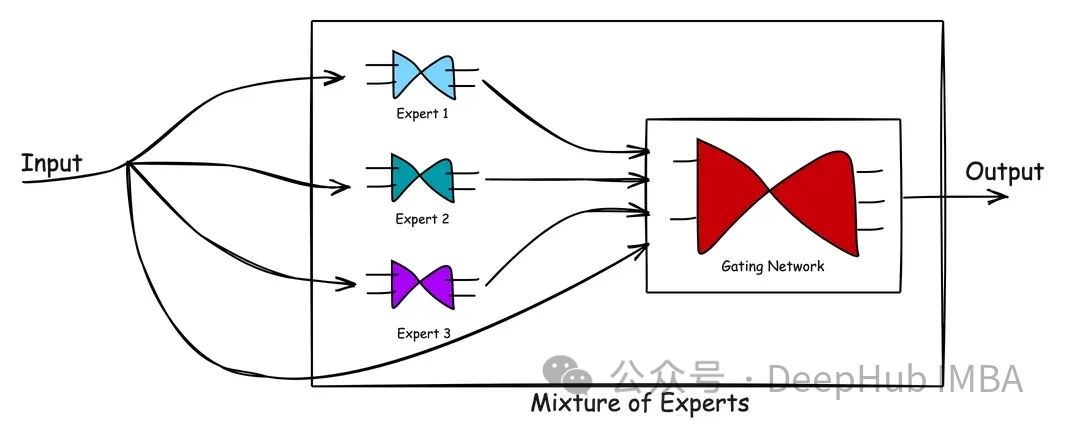
Gambar di atas menunjukkan aliran pemprosesan di KPM. Kelebihan model pakar campuran adalah kesederhanaannya. Dengan mempelajari ruang masalah yang kompleks dan reaksi pakar semasa menyelesaikan masalah, model KPM membantu menghasilkan penyelesaian yang lebih baik daripada seorang pakar. Rangkaian Gating bertindak sebagai pengurus yang berkesan, menilai senario dan menyerahkan tugas kepada pakar terbaik. Apabila data baharu dimasukkan, model boleh menyesuaikan diri dengan menilai semula kekuatan pakar terhadap input baharu, menghasilkan pendekatan pembelajaran yang fleksibel. Ringkasnya, model KPM memanfaatkan pengetahuan dan pengalaman pelbagai pakar untuk menyelesaikan masalah yang kompleks. Melalui pengurusan rangkaian berpagar, model boleh memilih pakar yang paling sesuai untuk mengendalikan tugas mengikut senario yang berbeza. Kelebihan pendekatan ini adalah keupayaannya untuk menghasilkan penyelesaian yang lebih baik daripada pakar tunggal dan fleksibilitinya untuk menyesuaikan diri dengan data input baharu. Secara keseluruhannya, model KPM merupakan kaedah yang berkesan dan mudah yang boleh digunakan untuk menyelesaikan pelbagai masalah yang kompleks.
MoE memberikan manfaat yang besar untuk menggunakan model pembelajaran mesin. Berikut adalah dua faedah yang ketara.
Kekuatan teras KPM terletak pada rangkaian pakarnya yang pelbagai dan profesional. Penetapan KPM boleh menangani masalah dalam pelbagai bidang dengan ketepatan yang tinggi, yang sukar dicapai dengan satu model.
MoE sememangnya boleh berskala. Apabila kerumitan tugas meningkat, lebih ramai pakar boleh disepadukan dengan lancar ke dalam sistem, mengembangkan skop kepakaran tanpa perlu menukar model pakar lain. Dalam erti kata lain, MoE boleh membungkus pakar yang telah terlatih ke dalam sistem pembelajaran mesin untuk membantu sistem menghadapi keperluan tugas yang semakin meningkat.
Model pakar campuran mempunyai aplikasi dalam banyak bidang, termasuk sistem pengesyoran, pemodelan bahasa dan pelbagai tugas ramalan yang kompleks. Terdapat khabar angin bahawa GPT-4 terdiri daripada berbilang pakar. Walaupun kami tidak dapat mengesahkan, model seperti gpt-4 akan memberikan hasil terbaik dengan memanfaatkan kuasa berbilang model melalui pendekatan KPM.
Kod Pytorch
Kami tidak akan membincangkan teknologi MOE yang digunakan dalam model besar seperti Mixtral 8x7B di sini, sebaliknya, kami menulis MOE tersuai yang boleh digunakan untuk sebarang tugasan kod Prinsip kerja KPM sangat membantu untuk memahami cara KPM berfungsi dalam model besar.
Di bawah ini kami akan memperkenalkan pelaksanaan kod PyTorch sekeping demi sekeping.
Import perpustakaan:
import torch import torch.nn as nn import torch.optim as optim
Tentukan model pakar:
class Expert(nn.Module): def __init__(self, input_dim, hidden_dim, output_dim): super(Expert, self).__init__() self.layer1 = nn.Linear(input_dim, hidden_dim) self.layer2 = nn.Linear(hidden_dim, output_dim) def forward(self, x): x = torch.relu(self.layer1(x)) return torch.softmax(self.layer2(x), dim=1)
Di sini kami mentakrifkan model pakar yang mudah, anda dapat melihat bahawa ia adalah mlp 2 lapisan, dan akhirnya menggunakan pengaktifan relu, dan akhirnya kebarangkalian pengelasan.
Tentukan model gating:
# Define the gating model class Gating(nn.Module): def __init__(self, input_dim,num_experts, dropout_rate=0.1): super(Gating, self).__init__() # Layers self.layer1 = nn.Linear(input_dim, 128) self.dropout1 = nn.Dropout(dropout_rate) self.layer2 = nn.Linear(128, 256) self.leaky_relu1 = nn.LeakyReLU() self.dropout2 = nn.Dropout(dropout_rate) self.layer3 = nn.Linear(256, 128) self.leaky_relu2 = nn.LeakyReLU() self.dropout3 = nn.Dropout(dropout_rate) self.layer4 = nn.Linear(128, num_experts) def forward(self, x): x = torch.relu(self.layer1(x)) x = self.dropout1(x) x = self.layer2(x) x = self.leaky_relu1(x) x = self.dropout2(x) x = self.layer3(x) x = self.leaky_relu2(x) x = self.dropout3(x) return torch.softmax(self.layer4(x), dim=1)
门控模型更复杂,有三个线性层和dropout层用于正则化以防止过拟合。它使用ReLU和LeakyReLU激活函数引入非线性。最后一层的输出大小等于专家的数量,并对这些输出应用softmax函数。输出权重,这样可以将专家的输出与之结合。
说明:其实门控网络,或者叫路由网络是MOE中最复杂的部分,因为它涉及到控制输入到那个专家模型,所以门控网络也有很多个设计方案,例如(如果我没记错的话)Mixtral 8x7B 只是取了8个专家中的top2。所以我们这里不详细讨论各种方案,只是介绍其基本原理和代码实现。
完整的MOE模型:
class MoE(nn.Module): def __init__(self, trained_experts): super(MoE, self).__init__() self.experts = nn.ModuleList(trained_experts) num_experts = len(trained_experts) # Assuming all experts have the same input dimension input_dim = trained_experts[0].layer1.in_features self.gating = Gating(input_dim, num_experts) def forward(self, x): # Get the weights from the gating network weights = self.gating(x) # Calculate the expert outputs outputs = torch.stack([expert(x) for expert in self.experts], dim=2) # Adjust the weights tensor shape to match the expert outputs weights = weights.unsqueeze(1).expand_as(outputs) # Multiply the expert outputs with the weights and # sum along the third dimension return torch.sum(outputs * weights, dim=2)
这里主要看前向传播的代码,通过输入计算出权重和每个专家给出输出的预测,最后使用权重将所有专家的结果求和最终得到模型的输出。
这个是不是有点像“集成学习”。
测试
下面我们来对我们的实现做个简单的测试,首先生成一个简单的数据集:
# Generate the dataset num_samples = 5000 input_dim = 4 hidden_dim = 32 # Generate equal numbers of labels 0, 1, and 2 y_data = torch.cat([ torch.zeros(num_samples // 3), torch.ones(num_samples // 3), torch.full((num_samples - 2 * (num_samples // 3),), 2)# Filling the remaining to ensure exact num_samples ]).long() # Biasing the data based on the labels x_data = torch.randn(num_samples, input_dim) for i in range(num_samples): if y_data[i] == 0: x_data[i, 0] += 1# Making x[0] more positive elif y_data[i] == 1: x_data[i, 1] -= 1# Making x[1] more negative elif y_data[i] == 2: x_data[i, 0] -= 1# Making x[0] more negative # Shuffle the data to randomize the order indices = torch.randperm(num_samples) x_data = x_data[indices] y_data = y_data[indices] # Verify the label distribution y_data.bincount() # Shuffle the data to ensure x_data and y_data remain aligned shuffled_indices = torch.randperm(num_samples) x_data = x_data[shuffled_indices] y_data = y_data[shuffled_indices] # Splitting data for training individual experts # Use the first half samples for training individual experts x_train_experts = x_data[:int(num_samples/2)] y_train_experts = y_data[:int(num_samples/2)] mask_expert1 = (y_train_experts == 0) | (y_train_experts == 1) mask_expert2 = (y_train_experts == 1) | (y_train_experts == 2) mask_expert3 = (y_train_experts == 0) | (y_train_experts == 2) # Select an almost equal number of samples for each expert num_samples_per_expert = \ min(mask_expert1.sum(), mask_expert2.sum(), mask_expert3.sum()) x_expert1 = x_train_experts[mask_expert1][:num_samples_per_expert] y_expert1 = y_train_experts[mask_expert1][:num_samples_per_expert] x_expert2 = x_train_experts[mask_expert2][:num_samples_per_expert] y_expert2 = y_train_experts[mask_expert2][:num_samples_per_expert] x_expert3 = x_train_experts[mask_expert3][:num_samples_per_expert] y_expert3 = y_train_experts[mask_expert3][:num_samples_per_expert] # Splitting the next half samples for training MoE model and for testing x_remaining = x_data[int(num_samples/2)+1:] y_remaining = y_data[int(num_samples/2)+1:] split = int(0.8 * len(x_remaining)) x_train_moe = x_remaining[:split] y_train_moe = y_remaining[:split] x_test = x_remaining[split:] y_test = y_remaining[split:] print(x_train_moe.shape,"\n", x_test.shape,"\n", x_expert1.shape,"\n", x_expert2.shape,"\n", x_expert3.shape)
这段代码创建了一个合成数据集,其中包含三个类标签——0、1和2。基于类标签对特征进行操作,从而在数据中引入一些模型可以学习的结构。
数据被分成针对个别专家的训练集、MoE模型和测试集。我们确保专家模型是在一个子集上训练的,这样第一个专家在标签0和1上得到很好的训练,第二个专家在标签1和2上得到更好的训练,第三个专家看到更多的标签2和0。
我们期望的结果是:虽然每个专家对标签0、1和2的分类准确率都不令人满意,但通过结合三位专家的决策,MoE将表现出色。
模型初始化和训练设置:
# Define hidden dimension output_dim = 3 hidden_dim = 32 epochs = 500 learning_rate = 0.001 # Instantiate the experts expert1 = Expert(input_dim, hidden_dim, output_dim) expert2 = Expert(input_dim, hidden_dim, output_dim) expert3 = Expert(input_dim, hidden_dim, output_dim) # Set up loss criterion = nn.CrossEntropyLoss() # Optimizers for experts optimizer_expert1 = optim.Adam(expert1.parameters(), lr=learning_rate) optimizer_expert2 = optim.Adam(expert2.parameters(), lr=learning_rate) optimizer_expert3 = optim.Adam(expert3.parameters(), lr=learning_rate)
实例化了专家模型和MoE模型。定义损失函数来计算训练损失,并为每个模型设置优化器,在训练过程中执行权重更新。
训练的步骤也非常简单
# Training loop for expert 1 for epoch in range(epochs):optimizer_expert1.zero_grad()outputs_expert1 = expert1(x_expert1)loss_expert1 = criterion(outputs_expert1, y_expert1)loss_expert1.backward()optimizer_expert1.step() # Training loop for expert 2 for epoch in range(epochs):optimizer_expert2.zero_grad()outputs_expert2 = expert2(x_expert2)loss_expert2 = criterion(outputs_expert2, y_expert2)loss_expert2.backward()optimizer_expert2.step() # Training loop for expert 3 for epoch in range(epochs):optimizer_expert3.zero_grad()outputs_expert3 = expert3(x_expert3)loss_expert3 = criterion(outputs_expert3, y_expert3)loss_expert3.backward()
每个专家使用基本的训练循环在不同的数据子集上进行单独的训练。循环迭代指定数量的epoch。
下面是我们MOE的训练
# Create the MoE model with the trained experts moe_model = MoE([expert1, expert2, expert3]) # Train the MoE model optimizer_moe = optim.Adam(moe_model.parameters(), lr=learning_rate) for epoch in range(epochs):optimizer_moe.zero_grad()outputs_moe = moe_model(x_train_moe)loss_moe = criterion(outputs_moe, y_train_moe)loss_moe.backward()optimizer_moe.step()
MoE模型是由先前训练过的专家创建的,然后在单独的数据集上进行训练。训练过程类似于单个专家的训练,但现在门控网络的权值在训练过程中更新。
最后我们的评估函数:
# Evaluate all models def evaluate(model, x, y):with torch.no_grad():outputs = model(x)_, predicted = torch.max(outputs, 1)correct = (predicted == y).sum().item()accuracy = correct / len(y)return accuracy
evaluate函数计算模型在给定数据上的精度(x代表样本,y代表预期标签)。准确度计算为正确预测数与预测总数之比。
结果如下:
accuracy_expert1 = evaluate(expert1, x_test, y_test) accuracy_expert2 = evaluate(expert2, x_test, y_test) accuracy_expert3 = evaluate(expert3, x_test, y_test) accuracy_moe = evaluate(moe_model, x_test, y_test) print("Expert 1 Accuracy:", accuracy_expert1) print("Expert 2 Accuracy:", accuracy_expert2) print("Expert 3 Accuracy:", accuracy_expert3) print("Mixture of Experts Accuracy:", accuracy_moe) #Expert 1 Accuracy: 0.466 #Expert 2 Accuracy: 0.496 #Expert 3 Accuracy: 0.378 #Mixture of Experts Accuracy: 0.614
可以看到
专家1正确预测了测试数据集中大约46.6%的样本的类标签。
专家2表现稍好,正确预测率约为49.6%。
专家3在三位专家中准确率最低,正确预测的样本约为37.8%。
而MoE模型显著优于每个专家,总体准确率约为61.4%。
总结
我们测试的输出结果显示了混合专家模型的强大功能。该模型通过门控网络将各个专家模型的优势结合起来,取得了比单个专家模型更高的精度。门控网络有效地学习了如何根据输入数据权衡每个专家的贡献,以产生更准确的预测。混合专家利用了各个模型的不同专业知识,在测试数据集上提供了更好的性能。
同时也说明我们可以在现有的任务上尝试使用MOE来进行测试,也可以得到更好的结果。
Atas ialah kandungan terperinci Melaksanakan Model Pakar Campuran (MoE) menggunakan PyTorch. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

