Baru-baru ini, sebuah kertas kerja telah dikeluarkan mengenai arxiv, yang memberikan tafsiran baru tentang prinsip matematik Transformer Kandungannya sangat panjang dan terdapat banyak pengetahuan Ia sangat disyorkan untuk membaca artikel asal.
Pada tahun 2017, "Perhatian adalah semua yang anda perlukan" yang diterbitkan oleh Vaswani et al menjadi peristiwa penting dalam pembangunan seni bina rangkaian saraf. Sumbangan teras kertas ini ialah mekanisme perhatian kendiri, iaitu inovasi yang membezakan Transformers daripada seni bina tradisional dan memainkan peranan penting dalam prestasi praktikalnya yang cemerlang. Malah, inovasi ini telah menjadi pemangkin utama untuk kemajuan kecerdasan buatan dalam bidang seperti penglihatan komputer dan pemprosesan bahasa semula jadi, di samping memainkan peranan penting dalam kemunculan model bahasa yang besar. Oleh itu, memahami Transformers, dan khususnya mekanisme yang memproses data perhatian kendiri, adalah bidang yang penting tetapi sebahagian besarnya kurang dipelajari. 
Alamat kertas: https://arxiv.org/pdf/2312.10794.pdfRangkaian saraf dalam (DNN) mempunyai ciri yang sama: data input diproses lapisan demi lapisan mengikut tertib, membentuk masa Sistem dinamik diskret (untuk kandungan tertentu, sila rujuk "Pembelajaran Mendalam" yang diterbitkan oleh MIT, juga dikenali sebagai "Buku Bunga" di China). Perspektif ini telah berjaya digunakan untuk memodelkan rangkaian sisa ke sistem dinamik berterusan masa, yang dipanggil persamaan pembezaan biasa saraf (ODE saraf). Dalam persamaan pembezaan pemalar ilahi, imej input 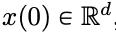 akan berkembang mengikut medan halaju yang berubah-ubah masa
akan berkembang mengikut medan halaju yang berubah-ubah masa 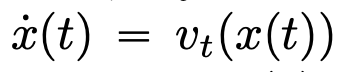 sepanjang selang masa (0, T). Oleh itu, DNN boleh dilihat sebagai Peta Alir
sepanjang selang masa (0, T). Oleh itu, DNN boleh dilihat sebagai Peta Alir 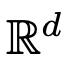 dari satu
dari satu  ke satu
ke satu 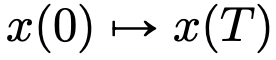 yang lain. Terdapat persamaan yang kukuh antara peta aliran walaupun dalam medan halaju
yang lain. Terdapat persamaan yang kukuh antara peta aliran walaupun dalam medan halaju 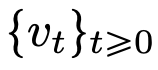 di bawah kekangan seni bina DNN klasik. Penyelidik mendapati Transformer sebenarnya adalah pemetaan aliran pada
di bawah kekangan seni bina DNN klasik. Penyelidik mendapati Transformer sebenarnya adalah pemetaan aliran pada 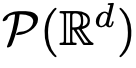 , iaitu pemetaan antara ruang ukuran kebarangkalian dimensi d (ruang ukuran kebarangkalian). Untuk melaksanakan pemetaan aliran ini yang menukar antara ruang metrik, Transformers perlu mewujudkan sistem zarah berinteraksi medan min. Secara khusus, setiap zarah (yang boleh difahami sebagai token dalam konteks pembelajaran mendalam) mengikuti aliran medan vektor, dan aliran bergantung pada ukuran empirikal semua zarah. Sebaliknya, persamaan menentukan evolusi ukuran empirikal zarah, proses yang boleh bertahan lama dan memerlukan perhatian yang berterusan. Pemerhatian utama penyelidik ialah zarah cenderung akhirnya bergumpal bersama. Fenomena ini amat ketara dalam tugasan pembelajaran seperti terbitan sehala (iaitu, meramal perkataan seterusnya dalam urutan). Metrik output mengekodkan taburan kebarangkalian token seterusnya dan sebilangan kecil hasil yang mungkin boleh ditapis berdasarkan hasil pengelompokan. Hasil penyelidikan artikel ini menunjukkan bahawa taburan had sebenarnya adalah jisim titik dan tidak ada kepelbagaian atau rawak, tetapi ini tidak konsisten dengan hasil pemerhatian sebenar. Paradoks yang jelas ini diselesaikan oleh fakta bahawa zarah wujud dalam keadaan berubah-ubah untuk jangka masa yang panjang. Seperti yang dapat dilihat daripada Rajah 2 dan 4, Transformer mempunyai dua skala masa yang berbeza: pada peringkat pertama, semua token dengan cepat membentuk beberapa kelompok, manakala pada peringkat kedua (jauh lebih perlahan daripada peringkat pertama), melalui Semasa proses penggabungan berpasangan kelompok, semua token akhirnya runtuh menjadi satu titik.
, iaitu pemetaan antara ruang ukuran kebarangkalian dimensi d (ruang ukuran kebarangkalian). Untuk melaksanakan pemetaan aliran ini yang menukar antara ruang metrik, Transformers perlu mewujudkan sistem zarah berinteraksi medan min. Secara khusus, setiap zarah (yang boleh difahami sebagai token dalam konteks pembelajaran mendalam) mengikuti aliran medan vektor, dan aliran bergantung pada ukuran empirikal semua zarah. Sebaliknya, persamaan menentukan evolusi ukuran empirikal zarah, proses yang boleh bertahan lama dan memerlukan perhatian yang berterusan. Pemerhatian utama penyelidik ialah zarah cenderung akhirnya bergumpal bersama. Fenomena ini amat ketara dalam tugasan pembelajaran seperti terbitan sehala (iaitu, meramal perkataan seterusnya dalam urutan). Metrik output mengekodkan taburan kebarangkalian token seterusnya dan sebilangan kecil hasil yang mungkin boleh ditapis berdasarkan hasil pengelompokan. Hasil penyelidikan artikel ini menunjukkan bahawa taburan had sebenarnya adalah jisim titik dan tidak ada kepelbagaian atau rawak, tetapi ini tidak konsisten dengan hasil pemerhatian sebenar. Paradoks yang jelas ini diselesaikan oleh fakta bahawa zarah wujud dalam keadaan berubah-ubah untuk jangka masa yang panjang. Seperti yang dapat dilihat daripada Rajah 2 dan 4, Transformer mempunyai dua skala masa yang berbeza: pada peringkat pertama, semua token dengan cepat membentuk beberapa kelompok, manakala pada peringkat kedua (jauh lebih perlahan daripada peringkat pertama), melalui Semasa proses penggabungan berpasangan kelompok, semua token akhirnya runtuh menjadi satu titik. 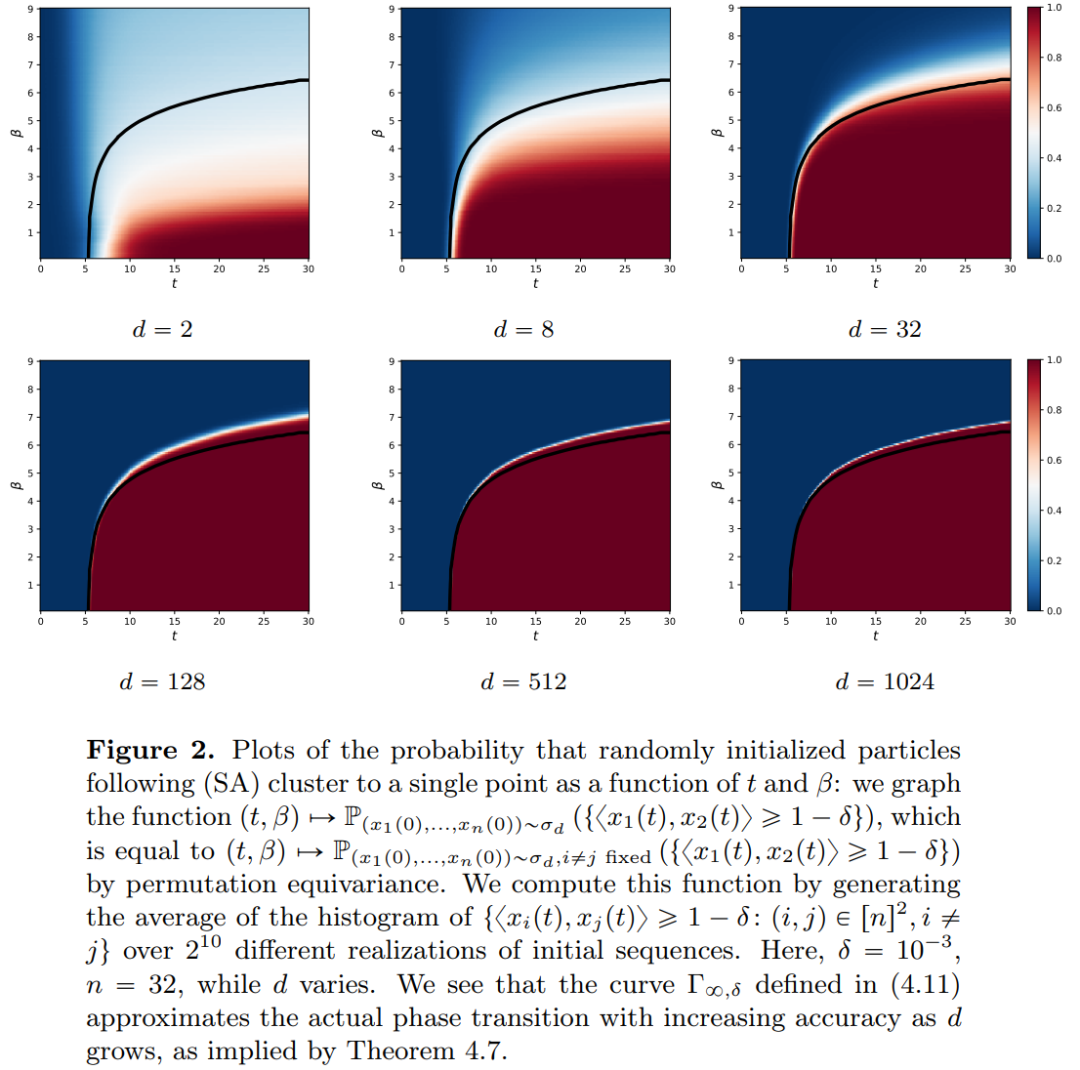
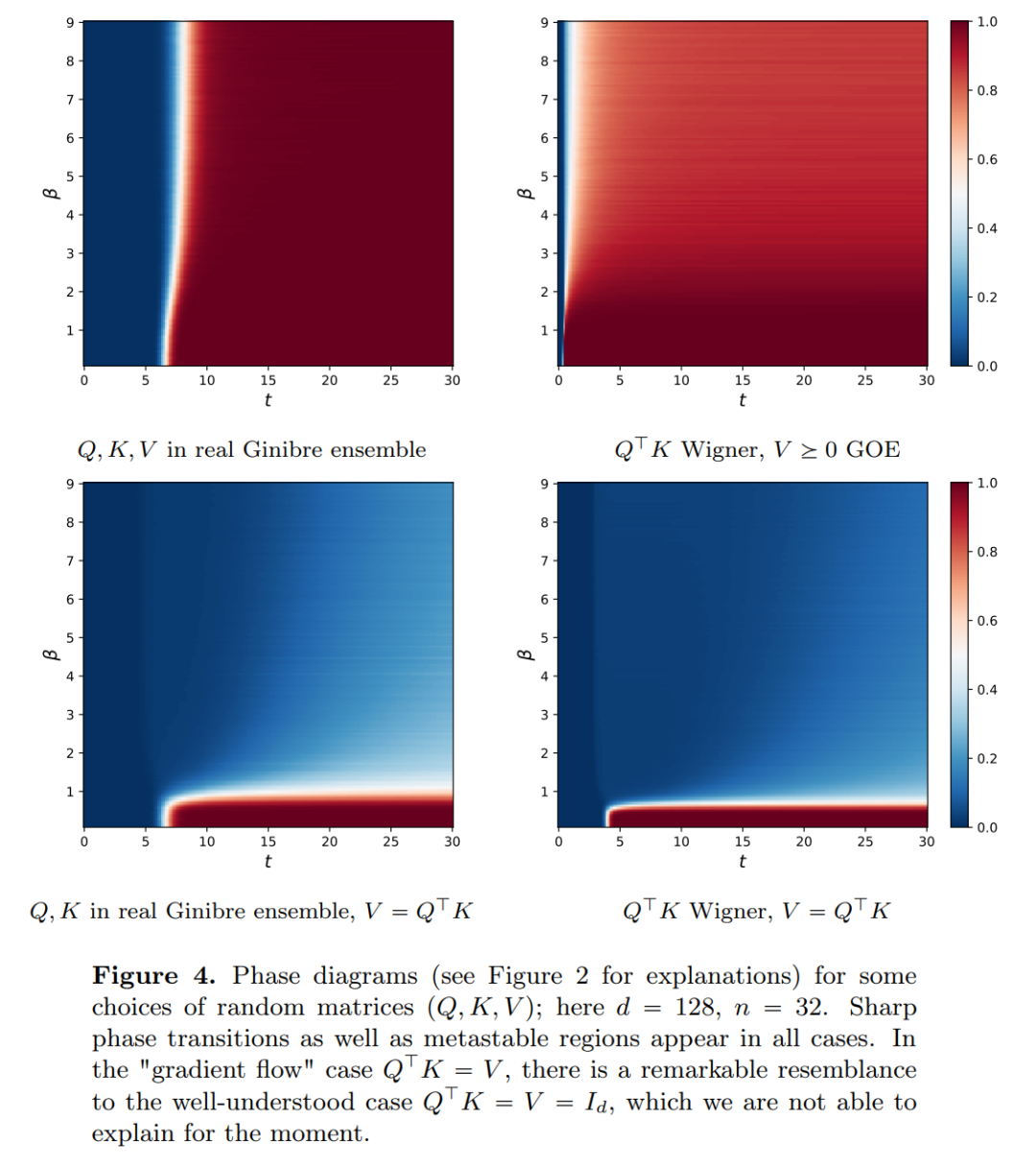
Matlamat artikel ini adalah dua kali ganda. Di satu pihak, Artikel ini bertujuan untuk menyediakan rangka kerja umum dan mudah difahami untuk mengkaji Transformers dari perspektif matematik. Khususnya, struktur sistem zarah berinteraksi ini membolehkan penyelidik membuat sambungan konkrit kepada topik yang telah ditetapkan dalam matematik, termasuk persamaan pengangkutan tak linear, aliran kecerunan Wasserstein, model tingkah laku kolektif, dan konfigurasi titik optimum pada sfera. Sebaliknya, kertas kerja ini menerangkan beberapa hala tuju penyelidikan yang menjanjikan, dengan tumpuan khusus pada fenomena pengelompokan dalam jangka masa yang panjang. Langkah-langkah hasil utama yang dicadangkan oleh penyelidik adalah baru, dan mereka juga menimbulkan soalan terbuka sepanjang kertas yang mereka anggap menarik. Sumbangan utama artikel ini dibahagikan kepada tiga bahagian. 
Bahagian 1: Permodelan. Artikel ini mentakrifkan model ideal seni bina Transformer yang menganggap bilangan lapisan sebagai pembolehubah masa berterusan. Pendekatan kepada abstraksi ini bukanlah baru dan serupa dengan pendekatan yang diambil oleh seni bina klasik seperti ResNets. Model artikel ini hanya memfokuskan pada dua komponen utama seni bina Transformer: mekanisme perhatian kendiri dan normalisasi lapisan. Normalisasi lapisan berkesan mengehadkan zarah pada ruang sfera unit 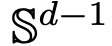 , manakala mekanisme perhatian kendiri mencapai gandingan tak linear antara zarah melalui pengukuran empirikal. Sebaliknya, ukuran empirikal berkembang mengikut persamaan pembezaan separa kesinambungan. Artikel ini juga memperkenalkan model alternatif yang lebih ringkas dan mudah digunakan untuk perhatian diri, aliran kecerunan Wasserstein bagi fungsi tenaga, dan sudah ada kaedah penyelidikan yang matang untuk konfigurasi titik optimum pada sfera fungsi tenaga. Bahagian 2: Pengelompokan. Dalam bahagian ini, penyelidik mencadangkan keputusan matematik baharu pada pengelompokan token dalam jangka masa yang lebih lama. Seperti yang ditunjukkan Teorem 4.1, dalam ruang dimensi tinggi, sekumpulan n zarah yang dimulakan secara rawak pada bola unit akan berkumpul menjadi satu titik pada
, manakala mekanisme perhatian kendiri mencapai gandingan tak linear antara zarah melalui pengukuran empirikal. Sebaliknya, ukuran empirikal berkembang mengikut persamaan pembezaan separa kesinambungan. Artikel ini juga memperkenalkan model alternatif yang lebih ringkas dan mudah digunakan untuk perhatian diri, aliran kecerunan Wasserstein bagi fungsi tenaga, dan sudah ada kaedah penyelidikan yang matang untuk konfigurasi titik optimum pada sfera fungsi tenaga. Bahagian 2: Pengelompokan. Dalam bahagian ini, penyelidik mencadangkan keputusan matematik baharu pada pengelompokan token dalam jangka masa yang lebih lama. Seperti yang ditunjukkan Teorem 4.1, dalam ruang dimensi tinggi, sekumpulan n zarah yang dimulakan secara rawak pada bola unit akan berkumpul menjadi satu titik pada 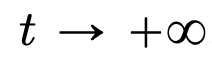 . Penerangan tepat penyelidik tentang kadar pengecutan gugusan zarah melengkapkan keputusan ini. Secara khusus, para penyelidik memplot histogram jarak antara semua zarah, serta titik masa apabila semua zarah hampir menyelesaikan pengelompokan (lihat Bahagian 4 artikel asal). Para penyelidik juga memperoleh hasil pengelompokan tanpa menganggap dimensi besar d (lihat Bahagian 5 artikel asal). Bahagian 3: Memandang ke hadapan. Kertas kerja ini mencadangkan barisan penyelidikan masa depan yang berpotensi dengan mengemukakan terutamanya soalan dalam bentuk soalan terbuka dan membuktikannya melalui pemerhatian berangka. Para penyelidik mula-mula memfokuskan pada kes dimensi d = 2 (lihat Bahagian 6 artikel asal) dan mengeluarkan sambungan dengan pengayun Kuramoto. Ia kemudian ditunjukkan secara ringkas bagaimana masalah sukar yang berkaitan dengan pengoptimuman sfera boleh diselesaikan dengan membuat pengubahsuaian yang mudah dan semula jadi pada model (lihat Bahagian 7 artikel asal). Bab berikut meneroka sistem zarah berinteraksi yang memungkinkan untuk melaraskan parameter dalam seni bina Transformer, yang mungkin membawa kepada aplikasi praktikal selanjutnya pada masa hadapan.
. Penerangan tepat penyelidik tentang kadar pengecutan gugusan zarah melengkapkan keputusan ini. Secara khusus, para penyelidik memplot histogram jarak antara semua zarah, serta titik masa apabila semua zarah hampir menyelesaikan pengelompokan (lihat Bahagian 4 artikel asal). Para penyelidik juga memperoleh hasil pengelompokan tanpa menganggap dimensi besar d (lihat Bahagian 5 artikel asal). Bahagian 3: Memandang ke hadapan. Kertas kerja ini mencadangkan barisan penyelidikan masa depan yang berpotensi dengan mengemukakan terutamanya soalan dalam bentuk soalan terbuka dan membuktikannya melalui pemerhatian berangka. Para penyelidik mula-mula memfokuskan pada kes dimensi d = 2 (lihat Bahagian 6 artikel asal) dan mengeluarkan sambungan dengan pengayun Kuramoto. Ia kemudian ditunjukkan secara ringkas bagaimana masalah sukar yang berkaitan dengan pengoptimuman sfera boleh diselesaikan dengan membuat pengubahsuaian yang mudah dan semula jadi pada model (lihat Bahagian 7 artikel asal). Bab berikut meneroka sistem zarah berinteraksi yang memungkinkan untuk melaraskan parameter dalam seni bina Transformer, yang mungkin membawa kepada aplikasi praktikal selanjutnya pada masa hadapan. Atas ialah kandungan terperinci Versi baharu yang didedahkan: Prinsip Matematik Transformer yang anda tidak pernah lihat sebelum ini. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

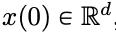 akan berkembang mengikut medan halaju yang berubah-ubah masa
akan berkembang mengikut medan halaju yang berubah-ubah masa 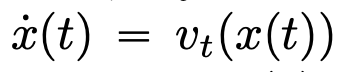 sepanjang selang masa (0, T). Oleh itu, DNN boleh dilihat sebagai Peta Alir
sepanjang selang masa (0, T). Oleh itu, DNN boleh dilihat sebagai Peta Alir 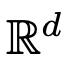 dari satu
dari satu  ke satu
ke satu  yang lain. Terdapat persamaan yang kukuh antara peta aliran walaupun dalam medan halaju
yang lain. Terdapat persamaan yang kukuh antara peta aliran walaupun dalam medan halaju 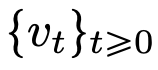 di bawah kekangan seni bina DNN klasik.
di bawah kekangan seni bina DNN klasik. 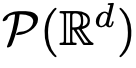 , iaitu pemetaan antara ruang ukuran kebarangkalian dimensi d (ruang ukuran kebarangkalian). Untuk melaksanakan pemetaan aliran ini yang menukar antara ruang metrik, Transformers perlu mewujudkan sistem zarah berinteraksi medan min.
, iaitu pemetaan antara ruang ukuran kebarangkalian dimensi d (ruang ukuran kebarangkalian). Untuk melaksanakan pemetaan aliran ini yang menukar antara ruang metrik, Transformers perlu mewujudkan sistem zarah berinteraksi medan min. 


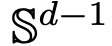 , manakala mekanisme perhatian kendiri mencapai gandingan tak linear antara zarah melalui pengukuran empirikal. Sebaliknya, ukuran empirikal berkembang mengikut persamaan pembezaan separa kesinambungan. Artikel ini juga memperkenalkan model alternatif yang lebih ringkas dan mudah digunakan untuk perhatian diri, aliran kecerunan Wasserstein bagi fungsi tenaga, dan sudah ada kaedah penyelidikan yang matang untuk konfigurasi titik optimum pada sfera fungsi tenaga.
, manakala mekanisme perhatian kendiri mencapai gandingan tak linear antara zarah melalui pengukuran empirikal. Sebaliknya, ukuran empirikal berkembang mengikut persamaan pembezaan separa kesinambungan. Artikel ini juga memperkenalkan model alternatif yang lebih ringkas dan mudah digunakan untuk perhatian diri, aliran kecerunan Wasserstein bagi fungsi tenaga, dan sudah ada kaedah penyelidikan yang matang untuk konfigurasi titik optimum pada sfera fungsi tenaga. 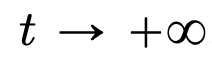 . Penerangan tepat penyelidik tentang kadar pengecutan gugusan zarah melengkapkan keputusan ini. Secara khusus, para penyelidik memplot histogram jarak antara semua zarah, serta titik masa apabila semua zarah hampir menyelesaikan pengelompokan (lihat Bahagian 4 artikel asal). Para penyelidik juga memperoleh hasil pengelompokan tanpa menganggap dimensi besar d (lihat Bahagian 5 artikel asal).
. Penerangan tepat penyelidik tentang kadar pengecutan gugusan zarah melengkapkan keputusan ini. Secara khusus, para penyelidik memplot histogram jarak antara semua zarah, serta titik masa apabila semua zarah hampir menyelesaikan pengelompokan (lihat Bahagian 4 artikel asal). Para penyelidik juga memperoleh hasil pengelompokan tanpa menganggap dimensi besar d (lihat Bahagian 5 artikel asal). 
