Ringkasan kerjasama antara Universiti Sains dan Teknologi China dan Universiti Normal Pertama: Mendedahkan bagaimana rangkaian tensor "kotak putih" boleh meningkatkan kebolehtafsiran dan kecekapan pembelajaran mesin kuantum

. berasal dari mekanik kuantum, adalah alat matematik yang matang. Ia telah menunjukkan kelebihan unik dalam membangunkan penyelesaian pembelajaran mesin "kotak putih" yang cekap

Baru-baru ini, Ran Shiju dari Capital Normal University dan Su Gang dari University of Chinese Academy of Sciences mendapat inspirasi daripada mekanik kuantum dan menyemak kaedah inovasi berasaskan TN, menyediakan penyelesaian yang menjanjikan kepada cabaran lama untuk menyelaraskan kebolehtafsiran dan kecekapan dalam pembelajaran mesin yang mendalam.

Di satu pihak, kebolehtafsiran TN ML boleh dicapai melalui asas teori yang kukuh berdasarkan maklumat kuantum dan fizik banyak badan. Sebaliknya, ekspresi TN yang berkuasa dan teknik pengkomputeran lanjutan yang dibangunkan dalam fizik kuantum banyak badan boleh mencapai kecekapan tinggi. Dengan perkembangan pesat komputer kuantum, TN dijangka menghasilkan penyelesaian baru yang boleh dijalankan pada perkakasan kuantum ke arah "AI kuantum" dalam masa terdekat

Semakan ini berdasarkan "

Rangkaian Tensor untuk Kuantum Boleh Ditafsir dan Cekap- Inspired Machine Learning

" bertajuk "

Intelligent Computing

" dan diterbitkan pada 17 November 2023.

Pautan kertas: https://spj.science.org/doi/10.34133/icomputing.0061

Model pembelajaran mendalam, terutamanya model rangkaian saraf, sering dipanggil "kotak keputusan" kerana mereka -proses membuat adalah kompleks dan sukar untuk dijelaskan. Rangkaian saraf kini merupakan model pembelajaran mendalam yang paling berkuasa. Contoh utama kuasanya ialah GPT. Walau bagaimanapun, disebabkan kekurangan kebolehjelasan, malah GPT menghadapi isu serius seperti keteguhan dan perlindungan privasi

Kekurangan kebolehjelasan model ini boleh menyebabkan kekurangan kepercayaan terhadap ramalan dan keputusan mereka, sekali gus mengehadkan penggunaannya dalam bidang penting Praktikal Aplikasi

Rangkaian tensor berdasarkan maklumat kuantum dan fizik berbilang badan menyediakan pendekatan "kotak putih" kepada ML. Para penyelidik berkata: "Rangkaian tensor memainkan peranan penting dalam menghubungkan konsep, teori dan kaedah kuantum dengan ML dan dengan berkesan melaksanakan ML berasaskan rangkaian tensor

Berkuasa "dari fizik kuantum" Alat matematik kotak putih." Fizik kuantum telah menghasilkan alat matematik "kotak putih" yang berkuasa.

Dengan perkembangan pesat pengkomputeran klasik dan kuantum, TN menyediakan idea baharu untuk mengatasi dilema antara kebolehtafsiran dan kecekapan. TN ditakrifkan sebagai penguncupan pelbagai tensor. Struktur rangkaiannya menentukan bagaimana tensor mengecut.

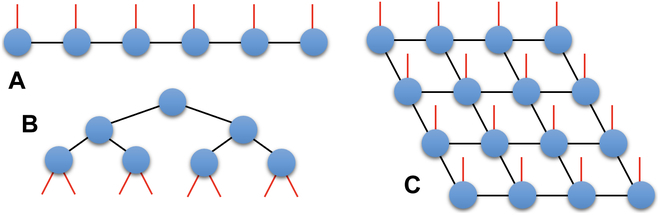
Dalam Rajah 1, perwakilan rajah bagi tiga jenis TN ditunjukkan. Tiga jenis ini ialah perwakilan keadaan produk matriks (MPS), TN pokok dan perwakilan keadaan pasangan terjerat unjuran (PEPS)

Rajah 1: Perwakilan grafik 3 jenis TN: (A) MPS, (B) )Tree TN dan (C)PEPS. (Sumber: kertas)

TN telah mencapai kejayaan yang luar biasa dalam bidang mekanik kuantum sebagai perwakilan yang cekap bagi keadaan sistem kuantum berskala besar. Dalam teori TN, keadaan yang memenuhi undang-undang kawasan entropi belitan boleh dianggarkan dengan cekap oleh perwakilan TN dengan dimensi ikatan terhingga.

Algoritma berasaskan MPS, termasuk kumpulan penormalan semula matriks ketumpatan dan pengekstrakan blok yang berubah-ubah masa, menunjukkan kecekapan yang ketara dalam mensimulasikan entropi belitan. Selain itu, MPS juga boleh mewakili banyak keadaan yang dibina secara buatan yang digunakan secara meluas dalam pemprosesan dan pengiraan maklumat kuantum, seperti keadaan Greenberger–Horne–Zeilinger dan keadaan W.

PEPS bermaksud undang-undang kawasan dalam dua dimensi dan lebih tinggi dan telah mencapai kejayaan besar dalam kajian sistem kuantum dimensi tinggi. Secara ringkasnya, undang-undang kawasan entropi belitan memberikan penjelasan intrinsik untuk perwakilan atau kuasa pengiraan TN dalam mensimulasikan sistem kuantum. Penjelasan ini juga terpakai kepada TN ML. Tambahan pula, TN sebagai alat berangka "kotak putih" (Mesin lahir), serupa dengan model kebarangkalian ML (klasik), boleh dijelaskan oleh tafsiran kebarangkalian kuantum Born (juga dikenali sebagai peraturan Born)

Gambar 2: MPS ( Borang Tensor Train) boleh digunakan untuk mewakili atau merumuskan sebilangan besar objek matematik dengan berkesan. (Dipetik daripada: kertas)

Kemajuan teknologi dalam pembelajaran mesin yang diilhamkan oleh kuantum (Kemajuan teknologi dalam pembelajaran mesin yang diilhamkan oleh kuantum)

TN menyediakan cara baharu untuk menyelesaikan dilema antara kebolehtafsiran dan kecekapan dalam pembelajaran mesin, berkat teori kukuh dan kaedah yang berkesan. Pada masa ini, terdapat dua baris penyelidikan yang sedang dibahaskan:

1. Bagaimana teori kuantum boleh berfungsi sebagai asas matematik untuk kebolehtafsiran TN ML?
2. Bagaimana kaedah TN mekanik kuantum dan teknologi pengkomputeran kuantum menghasilkan penyelesaian T N ML yang cekap?

Dalam kandungan ini, penyelidik memperkenalkan kemajuan menggalakkan baru-baru ini dalam ML berinspirasikan kuantum daripada perspektif pemetaan ciri, pemodelan dan ML berasaskan pengkomputeran kuantum, membuka perbincangan mengenai kedua-dua isu ini. Kemajuan ini berkait rapat dengan kelebihan menggunakan TN dalam meningkatkan kecekapan dan kebolehtafsiran. Pendekatan ML ini sering dipanggil "diilhamkan kuantum" kerana teori, model dan kaedahnya berasal daripada atau diilhamkan oleh fizik kuantum. Walau bagaimanapun, kami memerlukan lebih banyak usaha untuk membangunkan rangka kerja sistem untuk kebolehtafsiran berdasarkan fizik kuantum

Dalam jadual di bawah, kaedah utama pada TN ML dan hubungannya dengan kecekapan dan kebolehtafsiran diringkaskan

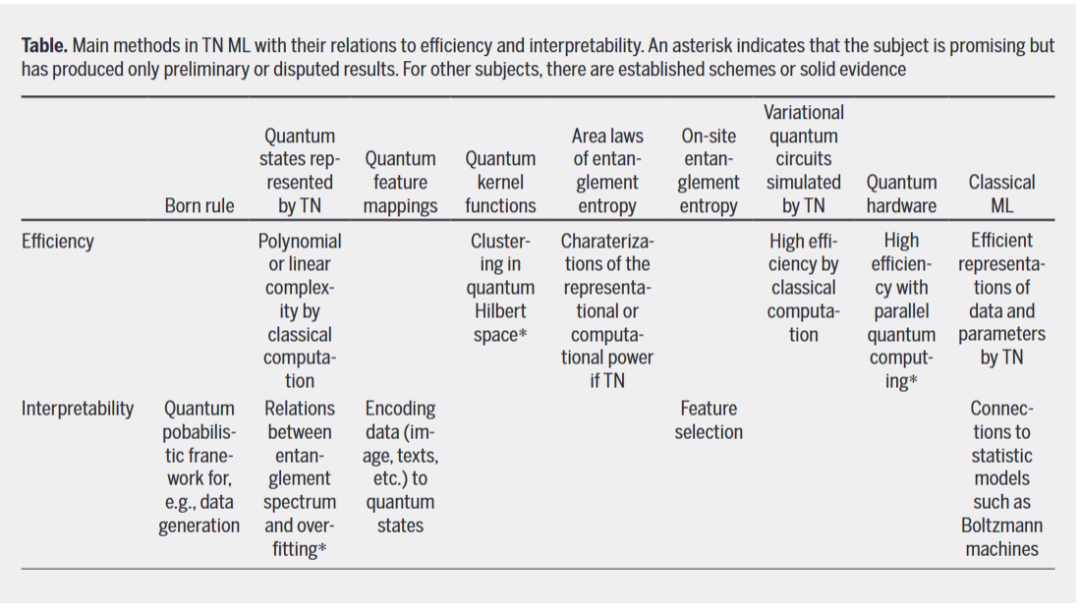
Rangkaian Teknikal yang Mempertingkatkan Klasik. Pembelajaran Mesin

Sebagai alat matematik asas, aplikasi rangkaian saraf dalam ML tidak terhad kepada yang mengikuti tafsiran probabilistik kuantum. Memandangkan TN boleh digunakan untuk mewakili dan mensimulasikan fungsi partition sistem stokastik klasik dengan berkesan, seperti model Ising dan Potts, hubungan antara mesin TN dan Boltzmann telah dikaji secara meluas.

TN juga digunakan untuk meningkatkan NN dan membangunkan model ML novel, mengabaikan sebarang tafsiran kebarangkalian. Ditulis semula ke dalam bahasa Cina: TN juga digunakan untuk meningkatkan NN dan membangunkan model ML baru, tanpa mengira sebarang tafsiran kebarangkalian

Berdasarkan asas yang sama, kaedah pemampatan model dicadangkan untuk menguraikan parameter variasi NN kepada TN atau secara langsung mewakili parameter variasi sebagai TN. Yang terakhir mungkin tidak memerlukan proses penguraian yang jelas, di mana parameter rangkaian saraf tidak dipulihkan kepada tensor tetapi terus kepada bentuk TT, pengendali produk matriks, atau TN dalam. Fungsi pengaktifan bukan linear telah ditambahkan pada TN untuk meningkatkan prestasi MLnya, menyamaratakan TN daripada model berbilang linear kepada model bukan linear.

Apa yang perlu ditulis semula ialah: Kesimpulan

Orang ramai telah lama berminat untuk menyelesaikan dilema antara kecekapan dan kebolehjelasan dalam kecerdasan buatan (terutamanya pembelajaran mesin yang mendalam). Dalam hal ini, kami menyemak kemajuan menggalakkan yang dibuat oleh TN, kaedah pembelajaran mesin berinspirasikan kuantum yang boleh ditafsir dan cekap

"Rama-rama N ML" dalam Rajah 3 menyenaraikan pencapaian TN dalam Kelebihan ML. Untuk ML yang diilhamkan kuantum, kelebihan TN boleh diringkaskan dalam dua aspek utama: teori kuantum untuk kebolehtafsiran dan kaedah kuantum untuk kecekapan yang lebih baik. Di satu pihak, TN membolehkan kami menggunakan statistik dan teori kuantum (cth., teori keterjeratan) untuk membina rangka kerja kebarangkalian untuk kebolehtafsiran yang mungkin melampaui apa yang boleh diterangkan oleh maklumat klasik atau teori statistik. Sebaliknya, algoritma TN mekanikal kuantum yang berkuasa dan teknologi pengkomputeran kuantum yang sangat dipertingkatkan akan membolehkan kaedah TN ML yang diilhamkan kuantum menjadi sangat cekap pada kedua-dua platform pengkomputeran klasik dan kuantum.

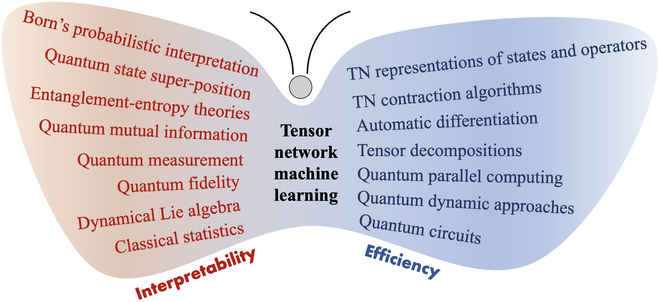
Rajah 3: "TN ML butterfly" meringkaskan 2 kelebihan unik: kebolehtafsiran berdasarkan teori kuantum (sayap kiri) dan kecekapan berdasarkan kaedah kuantum (sayap kanan). (Sumber: kertas)

Khususnya, dengan kemajuan ketara baru-baru ini dalam bidang GPT, terdapat lonjakan yang tidak pernah berlaku sebelum ini dalam kerumitan model dan kuasa pengkomputeran, yang telah membawa peluang dan cabaran baharu kepada TN ML. Dalam menghadapi GPT AI yang baru muncul, kebolehjelasan menjadi semakin berharga, bukan sahaja untuk meningkatkan kecekapan penyelidikan, tetapi juga untuk membolehkan aplikasi yang lebih baik dan kawalan yang lebih selamat

Dalam era NISQ semasa dan sebenar yang akan datang Dalam era pengkomputeran kuantum, TN dengan pantas berkembang menjadi alat matematik yang penting untuk meneroka kecerdasan buatan kuantum, dari pelbagai perspektif seperti teori, model, algoritma, perisian, perkakasan dan aplikasi

Kandungan rujukan: https://techxplore.com/news/2023 -11-tensor. -networks-efficiency-quantum-inspired-machine.html

Atas ialah kandungan terperinci Ringkasan kerjasama antara Universiti Sains dan Teknologi China dan Universiti Normal Pertama: Mendedahkan bagaimana rangkaian tensor "kotak putih" boleh meningkatkan kebolehtafsiran dan kecekapan pembelajaran mesin kuantum. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!