 Peranti teknologi
Peranti teknologi AI
AI Sembilan algoritma pengelompokan untuk meneroka pembelajaran mesin tanpa pengawasan
Sembilan algoritma pengelompokan untuk meneroka pembelajaran mesin tanpa pengawasanSembilan algoritma pengelompokan untuk meneroka pembelajaran mesin tanpa pengawasan
Hari ini, saya ingin berkongsi dengan anda kaedah pengelompokan pembelajaran tanpa pengawasan yang biasa dalam pembelajaran mesin
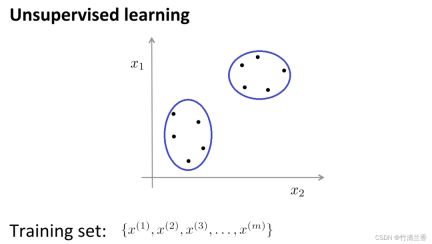
Dalam pembelajaran tanpa pengawasan, data kami tidak membawa sebarang label, jadi apa yang perlu kami lakukan dalam pembelajaran tanpa pengawasan adalah untuk Siri data tidak berlabel ini ialah input ke dalam algoritma, dan kemudian algoritma dibenarkan untuk mencari beberapa struktur yang tersirat dalam data Melalui data dalam rajah di bawah, satu struktur yang boleh didapati ialah titik dalam set data boleh dibahagikan kepada dua set titik berasingan. . (kluster), algoritma yang boleh mengelilingi kluster ini (cluster) dipanggil algoritma pengelompokan.
Aplikasi algoritma pengelompokan
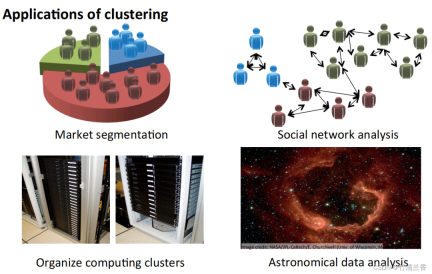
- Segmentasi pasaran: Kumpulan maklumat pelanggan dalam pangkalan data mengikut pasaran, untuk mencapai jualan atau peningkatan perkhidmatan yang berasingan mengikut pasaran yang berbeza.
- Analisis rangkaian sosial: Cari kumpulan rapat dengan menghantar e-mel kepada orang yang paling kerap dihubungi dan kenalan mereka yang paling kerap.
- Atur gugusan komputer: Dalam pusat data, gugusan komputer sering berfungsi bersama dan boleh digunakan untuk menyusun semula sumber, menyusun semula rangkaian, mengoptimumkan pusat data dan menyampaikan data.
- Fahami komposisi Bima Sakti: Gunakan maklumat ini untuk mempelajari sesuatu tentang astronomi.
Matlamat analisis kelompok adalah untuk membahagikan pemerhatian kepada kumpulan ("cluster") supaya perbezaan berpasangan antara pemerhatian yang diberikan kepada kelompok yang sama cenderung lebih kecil daripada perbezaan antara pemerhatian dalam kelompok yang berbeza. Algoritma pengelompokan dibahagikan kepada tiga jenis berbeza: algoritma gabungan, pemodelan hibrid dan carian corak. . Bisecting K- Means
DBSCANOPTIK
BIRCH- K-means
- Algoritma K-means ialah salah satu kaedah pengelompokan yang paling popular pada masa ini.
- K-means telah dicadangkan oleh Stuart Lloyd dari Bell Labs pada tahun 1957. Ia pada asalnya digunakan untuk modulasi kod nadi Tidak sampai tahun 1982 algoritma itu diumumkan kepada orang ramai. Pada tahun 1965, Edward W. Forgy menerbitkan algoritma yang sama, jadi K-Means kadangkala dipanggil Lloyd-Forgy.
- Masalah pengelompokan biasanya memerlukan pemprosesan set set data tidak berlabel dan memerlukan algoritma untuk membahagikan data ini secara automatik kepada subset atau kelompok yang berkait rapat. Pada masa ini, algoritma pengelompokan yang paling popular dan digunakan secara meluas ialah algoritma K-means
- Pemahaman intuitif algoritma K-means:
Katakan terdapat set data tidak berlabel di atas), dan kami Jika anda ingin membahagikannya kepada dua kluster, kini laksanakan algoritma K-means Operasi khusus adalah seperti berikut:
Langkah pertama ialah menjana dua mata secara rawak (kerana anda ingin berkelompok. data kepada dua kategori) (kanan gambar di atas), kedua-dua titik ini dipanggil cluster centroids.
Langkah kedua ialah melakukan gelung dalaman bagi algoritma K-means. Algoritma K-means ialah algoritma lelaran yang melakukan dua perkara Yang pertama ialah penugasan kelompok dan yang kedua ialah gerakkan centroid. Langkah pertama dalam gelung dalaman adalah untuk melakukan tugasan kluster, iaitu, melintasi setiap sampel, dan kemudian menetapkan setiap titik ke pusat kluster yang berbeza berdasarkan jarak dari setiap titik ke pusat kluster. kes ini adalah untuk mengulangi set data dan mewarna setiap titik merah atau biru. . penetapan kluster dibuat berdasarkan jarak, dan proses ini digelung secara berterusan sehingga kedudukan pusat kluster tidak lagi berubah dengan lelaran, dan warna titik tidak lagi berubah. Pada masa ini boleh dikatakan bahawa K-means telah menyelesaikan agregasi. Algoritma ini melakukan kerja yang cukup baik untuk mencari dua kelompok dalam data
Kelebihan algoritma K-Means:
Mudah dan mudah difahami, kelajuan pengiraan pantas, dan sesuai untuk set data berskala besar.
Kelemahan:
- Sebagai contoh, keupayaan pemprosesan untuk kluster bukan sfera adalah lemah, ia mudah dipengaruhi oleh pemilihan pusat kluster awal, dan bilangan kluster K perlu dinyatakan terlebih dahulu.
- Selain itu, apabila terdapat bunyi bising atau outlier antara titik data, algoritma K-Means mungkin menetapkannya kepada kelompok yang salah.
Hierarki Pengelompokan
Hierarki Pengelompokan ialah operasi pengelompokan set sampel mengikut tahap tertentu. Tahap di sini sebenarnya merujuk kepada takrifan jarak tertentu
Tujuan utama pengelompokan adalah untuk mengurangkan bilangan pengelasan, jadi ia adalah serupa dalam tingkah laku proses dendrogram yang secara beransur-ansur menghampiri dari nod daun ke nod akar. . Jenis ini Tingkah laku juga dipanggil "bottom-up"
Lebih popular, pengelompokan hierarki menganggap gugusan yang dimulakan sebagai nod pepohon Pada setiap langkah lelaran, dua gugusan yang serupa digabungkan menjadi gugusan besar baharu dicipta dan proses ini diulang sehingga akhirnya hanya tinggal satu kelompok (nod akar).
Strategi pengelompokan hierarki terbahagi kepada dua paradigma asas: agregasi (bawah ke atas) dan pembahagian (atas ke bawah).
Kebalikan daripada pengelompokan hierarki ialah pengelompokan divisive, juga dikenali sebagai DIANA (Analisis Pembahagian), yang proses kelakuannya adalah "atas-bawah"
Hasil algoritma K-means bergantung pada kelompok yang dipilih untuk mencari . Peruntukan bilangan kelas dan konfigurasi permulaan. Sebaliknya, kaedah pengelompokan hierarki tidak memerlukan spesifikasi sedemikian. Sebaliknya, mereka memerlukan pengguna untuk menentukan ukuran ketidaksamaan antara kumpulan pemerhatian (berpisah) berdasarkan ketidaksamaan berpasangan antara dua set pemerhatian. Seperti namanya, kaedah pengelompokan hierarki menghasilkan perwakilan hierarki di mana kelompok di setiap peringkat dicipta dengan menggabungkan kelompok di peringkat bawah seterusnya. Pada peringkat terendah, setiap kelompok mengandungi satu pemerhatian. Pada tahap tertinggi, hanya satu gugusan mengandungi semua data
Kelebihan:
- Persamaan jarak dan peraturan mudah ditakrifkan dan mempunyai sedikit sekatan
- tidak perlu menentukan bilangan; ;
- boleh menemui hubungan hierarki kelas
- boleh dikelompokkan ke dalam bentuk lain.
Kelemahan:
- Kerumitan pengiraan terlalu tinggi;
- Nilai tunggal ke dalam 🜎 kemungkinan besar juga boleh memberi impak kepada; .
- Agglomerative Clustering
Kandungan yang ditulis semula ialah: Agglomerative Clustering ialah algoritma pengelompokan bawah ke atas yang menganggap setiap titik data sebagai gugusan awal dan secara beransur-ansur menggabungkannya Mereka membentuk gugusan yang lebih besar sehingga keadaan berhenti dipenuhi. Dalam algoritma ini, setiap titik data pada mulanya dianggap sebagai gugusan yang berasingan, dan kemudian gugusan digabungkan secara beransur-ansur sehingga semua titik data digabungkan menjadi satu gugusan besar
Kelebihan:
Sesuai untuk bentuk dan saiz yang berbeza kluster, dan tidak perlu menyatakan bilangan kluster terlebih dahulu.
- Algoritma juga boleh mengeluarkan hierarki pengelompokan untuk analisis dan visualisasi yang mudah.
- Kelemahan:
Kerumitan pengiraan adalah tinggi, terutamanya apabila memproses set data berskala besar, ia memerlukan sejumlah besar sumber pengkomputeran dan ruang storan.
- Algoritma ini juga sensitif terhadap pemilihan kluster awal, yang mungkin membawa kepada hasil kluster yang berbeza.
- Perambatan Perkaitan
Kandungan yang diubah suai: Algoritma Perambatan Perkaitan (AP) biasanya diterjemahkan sebagai Algoritma Perambatan Perkaitan atau Algoritma Perambatan Kehampiran
penggabungan algoritma berdasarkan "eksekusi" s " (titik perwakilan) dan "kelompok" (kelompok) dalam data. Tidak seperti algoritma pengelompokan tradisional seperti K-Means, Perambatan Perkaitan tidak perlu menentukan bilangan kelompok terlebih dahulu, dan ia juga tidak perlu memulakan pusat kelompok secara rawak Sebaliknya, ia memperoleh hasil pengelompokan akhir dengan mengira persamaan antara titik data.
Kelebihan:
- Tidak perlu menyatakan bilangan keluarga kluster akhir
- Titik data sedia ada digunakan sebagai pusat kluster terakhir dan bukannya menjana pusat kluster baharu.
- Model tidak sensitif kepada nilai awal data.
- Tiada keperluan untuk simetri data matriks persamaan awal.
- Berbanding dengan kaedah pengelompokan k-centers, ralat ralat kuasa dua hasil adalah lebih kecil.
Kelemahan:
- Algoritma ini mempunyai kerumitan pengiraan yang tinggi dan memerlukan banyak ruang storan dan sumber pengkomputeran
- kebolehan pemprosesan dan pengeluaran yang lemah;
Shifting clustering ialah algoritma pengelompokan bukan parametrik berasaskan ketumpatan ialah mencari lokasi dengan ketumpatan tertinggi titik data (dipanggil "maksimum tempatan" atau "puncak"). , untuk mengenal pasti kelompok dalam data. Teras algoritma ini adalah untuk menganggarkan ketumpatan setempat bagi setiap titik data, dan menggunakan keputusan anggaran ketumpatan untuk mengira arah dan jarak pergerakan titik data
Kelebihan:
- Tidak perlu untuk menentukan bilangan kelompok, Dan ia juga mempunyai hasil yang baik untuk kelompok dengan bentuk yang kompleks.
- Algoritma ini juga mampu mengendalikan data bising dengan berkesan.
Kelemahan:
- Kerumitan pengiraan adalah tinggi, terutamanya apabila memproses set data berskala besar, yang memerlukan sejumlah besar sumber pengkomputeran dan ruang storan ini; parameter Pemilihan adalah agak sensitif dan memerlukan pelarasan dan pengoptimuman parameter.
- Bisecting K-Means
Bisecting K-Means ialah algoritma pengelompokan hierarki berdasarkan algoritma K-Means . , gunakan algoritma K-Means pada setiap subkluster secara berasingan, dan ulangi proses ini sehingga bilangan kluster yang telah ditetapkan dicapai.
Algoritma mula-mula merawat semua titik data sebagai gugusan awal, kemudian menggunakan algoritma K-Means pada gugusan, membahagikan gugusan itu kepada dua subkluster dan mengira jumlah ralat kuasa dua (SSE) untuk setiap sub- kelompok. Kemudian, subkluster dengan jumlah ralat kuasa dua terbesar dipilih dan dibahagikan kepada dua subkluster sekali lagi, dan proses ini diulang sehingga bilangan kluster yang telah ditetapkan dicapai.
Kelebihan:
mempunyai ketepatan dan kestabilan yang tinggi, boleh mengendalikan set data berskala besar dengan berkesan, dan tidak perlu menyatakan bilangan awal kelompok.
- Algoritma ini juga mampu mengeluarkan hierarki pengelompokan untuk analisis dan visualisasi yang mudah.
- Kelemahan:
Kerumitan pengiraan adalah tinggi, terutamanya apabila memproses set data berskala besar, ia memerlukan banyak sumber pengkomputeran dan ruang storan.
- Selain itu, algoritma ini juga sensitif terhadap pemilihan kelompok awal, yang mungkin membawa kepada hasil pengelompokan yang berbeza.
- DBSCAN
Algoritma pengelompokan spatial berasaskan ketumpatan DBSCAN (Pengkelompokan Spatial Berasaskan Ketumpatan Aplikasi dengan Bunyi) ialah kaedah pengelompokan biasa dengan bunyi
tetapi tiada pergantungan pada kaedah ketumpatan pada ketumpatan. Oleh itu, ia boleh mengatasi kelemahan bahawa algoritma berasaskan jarak hanya boleh mencari kelompok "sfera" Idea teras algoritma DBSCAN ialah: untuk titik data tertentu, jika ketumpatannya mencapai ambang tertentu, ia tergolong dalam kelompok. ; jika tidak, ia dianggap sebagai titik bunyi.
Kelebihan:
- Algoritma jenis ini boleh mengatasi kelemahan algoritma berasaskan jarak yang hanya boleh mencari gugusan "bulatan" (cembung)
- tidak sensitif kepada sebarang bentuk, dan gugusan; data bising;
- Tidak perlu menyatakan bilangan gugusan kelas
- Hanya terdapat dua parameter dalam algoritma, jejari imbasan (eps) dan bilangan minimum mata yang disertakan (min_samples).
Kelemahan:
- Kerumitan pengiraan, tanpa sebarang pengoptimuman, kerumitan masa algoritma ialah O(N^{2}), biasanya pokok R, pokok k-d;, bola boleh digunakan
- indeks pokok untuk mempercepatkan pengiraan dan mengurangkan kerumitan masa algoritma kepada O(Nlog(N));
- sangat dipengaruhi oleh EPS. Apabila ketumpatan pengedaran data dalam kelas tidak sekata, apabila eps kecil, gugusan dengan ketumpatan kecil akan dibahagikan kepada berbilang gugusan dengan sifat yang serupa apabila eps besar, gugusan yang lebih rapat dan padat akan digabungkan menjadi satu gugusan. Dalam kes data dimensi tinggi, pemilihan eps adalah lebih sukar kerana kutukan dimensi;
- tidak sesuai untuk perbezaan kepekatan set data Sangat besar, kerana sukar untuk memilih eps dan metrik.
- OPTIK
Idea teras algoritma OPTIK adalah untuk mengira jarak antara titik data tertentu dan titik lain untuk menentukan kebolehcapaiannya pada ketumpatan dan membina peta jarak berasaskan kepadatan. Kemudian, dengan mengimbas peta jarak ini, bilangan gugusan ditentukan secara automatik dan setiap gugusan dibahagikan
Kelebihan:
Dapat menentukan bilangan gugusan dan mengendalikan gugusan dalam sebarang bentuk secara automatik, dan Able untuk mengendalikan data bising dengan berkesan.
- Algoritma ini juga mampu mengeluarkan hierarki pengelompokan untuk analisis dan visualisasi yang mudah.
- Kelemahan:
Kerumitan pengiraan adalah tinggi, terutamanya apabila memproses set data berskala besar, ia memerlukan sejumlah besar sumber pengkomputeran dan ruang storan.
- Algoritma ini mungkin menghasilkan keputusan pengelompokan yang lemah untuk set data dengan perbezaan ketumpatan yang besar. . Algoritma BIRCH adalah untuk mengurangkan saiz data secara beransur-ansur melalui pengelompokan hierarki set data, dan akhirnya mendapatkan struktur kelompok. Algoritma BIRCH menggunakan struktur yang serupa dengan pokok B, dipanggil pokok CF, yang boleh memasukkan dan memadam subkluster dengan cepat dan boleh diseimbangkan secara automatik untuk memastikan kualiti dan kecekapan kluster
- Kelebihan:
Boleh memproses set data berskala besar dengan cepat, dan mempunyai hasil yang baik untuk kelompok bentuk arbitrari.
Algoritma ini juga mempunyai toleransi kesalahan yang baik untuk data bising dan outlier.
Kelemahan:
- Untuk set data dengan perbezaan ketumpatan yang besar, ia mungkin membawa kepada hasil pengelompokan yang buruk
- kesannya juga bukan pada set data berdimensi tinggi yang lain; .
Atas ialah kandungan terperinci Sembilan algoritma pengelompokan untuk meneroka pembelajaran mesin tanpa pengawasan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Pembangunan permainan AI memasuki era agentiknya dengan portal pemimpi UphealMay 02, 2025 am 11:17 AM
Pembangunan permainan AI memasuki era agentiknya dengan portal pemimpi UphealMay 02, 2025 am 11:17 AMPermainan Upheaval: Merevolusi Pembangunan Permainan Dengan Ejen AI Upheaval, sebuah studio pembangunan permainan yang terdiri daripada veteran dari gergasi industri seperti Blizzard dan Obsidian, bersedia untuk merevolusikan penciptaan permainan dengan platfor AI yang inovatif
 Uber mahu menjadi kedai Robotaxi anda, adakah pembekal membiarkan mereka?May 02, 2025 am 11:16 AM
Uber mahu menjadi kedai Robotaxi anda, adakah pembekal membiarkan mereka?May 02, 2025 am 11:16 AMStrategi Robotaxi Uber: ekosistem perjalanan untuk kenderaan autonomi Pada persidangan Curbivore baru-baru ini, Uber's Richard Willder melancarkan strategi mereka untuk menjadi platform perjalanan untuk penyedia Robotaxi. Memanfaatkan kedudukan dominan mereka di
 Ejen AI bermain permainan video akan mengubah robot masa depanMay 02, 2025 am 11:15 AM
Ejen AI bermain permainan video akan mengubah robot masa depanMay 02, 2025 am 11:15 AMPermainan video terbukti menjadi alasan ujian yang tidak ternilai untuk penyelidikan AI canggih, terutamanya dalam pembangunan agen autonomi dan robot dunia nyata, malah berpotensi menyumbang kepada pencarian kecerdasan umum buatan (AGI). A
 Kompleks Perindustrian Permulaan, VC 3.0, dan Manifesto James CurrierMay 02, 2025 am 11:14 AM
Kompleks Perindustrian Permulaan, VC 3.0, dan Manifesto James CurrierMay 02, 2025 am 11:14 AMKesan landskap modal teroka yang berkembang jelas dalam media, laporan kewangan, dan perbualan setiap hari. Walau bagaimanapun, akibat khusus untuk pelabur, permulaan, dan dana sering diabaikan. Venture Capital 3.0: Paradigma
 Adobe mengemas kini Cloud Creative dan Firefly di Adobe Max London 2025May 02, 2025 am 11:13 AM
Adobe mengemas kini Cloud Creative dan Firefly di Adobe Max London 2025May 02, 2025 am 11:13 AMAdobe Max London 2025 menyampaikan kemas kini penting kepada Awan Kreatif dan Firefly, mencerminkan peralihan strategik ke arah aksesibiliti dan AI generatif. Analisis ini menggabungkan pandangan dari taklimat pra-peristiwa dengan kepimpinan Adobe. (Nota: Adob
 Segala -galanya Meta diumumkan di LlamaconMay 02, 2025 am 11:12 AM
Segala -galanya Meta diumumkan di LlamaconMay 02, 2025 am 11:12 AMPengumuman Llamacon Meta mempamerkan strategi AI yang komprehensif yang direka untuk bersaing secara langsung dengan sistem AI yang tertutup seperti OpenAI, sementara pada masa yang sama mencipta aliran pendapatan baru untuk model sumber terbuka. Pendekatan beragam ini mensasarkan bo
 Kontroversi pembuatan bir atas cadangan bahawa AI tidak lebih dari sekadar teknologi biasaMay 02, 2025 am 11:10 AM
Kontroversi pembuatan bir atas cadangan bahawa AI tidak lebih dari sekadar teknologi biasaMay 02, 2025 am 11:10 AMTerdapat perbezaan yang serius dalam bidang kecerdasan buatan pada kesimpulan ini. Ada yang menegaskan bahawa sudah tiba masanya untuk mendedahkan "pakaian baru Maharaja", sementara yang lain menentang idea bahawa kecerdasan buatan hanyalah teknologi biasa. Mari kita bincangkannya. Analisis terobosan AI yang inovatif ini adalah sebahagian daripada lajur Forbes yang berterusan yang meliputi kemajuan terkini dalam bidang AI, termasuk mengenal pasti dan menjelaskan pelbagai kerumitan AI yang berpengaruh (klik di sini untuk melihat pautan). Kecerdasan Buatan sebagai Teknologi Biasa Pertama, beberapa pengetahuan asas diperlukan untuk meletakkan asas untuk perbincangan penting ini. Pada masa ini terdapat banyak penyelidikan yang didedikasikan untuk terus membangunkan kecerdasan buatan. Matlamat keseluruhan adalah untuk mencapai kecerdasan umum buatan (AGI) dan juga kecerdasan super buatan (AS)
 Model warga, mengapa nilai AI adalah ukuran perniagaan seterusnyaMay 02, 2025 am 11:09 AM
Model warga, mengapa nilai AI adalah ukuran perniagaan seterusnyaMay 02, 2025 am 11:09 AMKeberkesanan model AI syarikat kini merupakan penunjuk prestasi utama. Sejak ledakan AI, AI generatif telah digunakan untuk segala -galanya daripada menyusun jemputan ulang tahun untuk menulis kod perisian. Ini telah membawa kepada percambahan mod bahasa


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Penyesuai Pelayan SAP NetWeaver untuk Eclipse
Integrasikan Eclipse dengan pelayan aplikasi SAP NetWeaver.

VSCode Windows 64-bit Muat Turun
Editor IDE percuma dan berkuasa yang dilancarkan oleh Microsoft

SublimeText3 Linux versi baharu
SublimeText3 Linux versi terkini

mPDF
mPDF ialah perpustakaan PHP yang boleh menjana fail PDF daripada HTML yang dikodkan UTF-8. Pengarang asal, Ian Back, menulis mPDF untuk mengeluarkan fail PDF "dengan cepat" dari tapak webnya dan mengendalikan bahasa yang berbeza. Ia lebih perlahan dan menghasilkan fail yang lebih besar apabila menggunakan fon Unicode daripada skrip asal seperti HTML2FPDF, tetapi menyokong gaya CSS dsb. dan mempunyai banyak peningkatan. Menyokong hampir semua bahasa, termasuk RTL (Arab dan Ibrani) dan CJK (Cina, Jepun dan Korea). Menyokong elemen peringkat blok bersarang (seperti P, DIV),

Dreamweaver CS6
Alat pembangunan web visual






