Cara melaksanakan pengecaman kedudukan radar FMCW secara elegan (IROS2023)

Hello semua, nama saya Yuan Jianhao, dan saya sangat gembira untuk datang ke platform Heart of Autonomous Driving untuk berkongsi kerja kami mengenai pengecaman kedudukan radar di IROS2023.

Penempatan menggunakan radar Frequency Modulated Continuous Wave (FMCW) semakin mendapat perhatian kerana rintangan yang wujud terhadap persekitaran yang mencabar. Walau bagaimanapun, artifak kompleks proses pengukuran radar memerlukan anggaran ketidakpastian yang sesuai - untuk memastikan penggunaan yang selamat dan boleh dipercayai bagi modaliti sensor yang menjanjikan ini. Dalam kerja ini, kami mencadangkan sistem pengurusan peta berbilang sesi yang membina peta "optimum" berdasarkan sifat varians yang dipelajari dalam ruang benam untuk penyetempatan selanjutnya. Menggunakan sifat varians yang sama, kami juga mencadangkan kaedah baharu untuk secara introspektif menolak pertanyaan penentududukan yang mungkin tidak betul. Untuk tujuan ini, kami menggunakan pembelajaran metrik sedar bunyi yang teguh yang kedua-duanya mengeksploitasi variasi skala masa pendek dalam data radar di sepanjang laluan pemanduan (untuk penambahan data) dan meramalkan ketidakpastian hiliran dalam pengecaman kedudukan berasaskan ruang metrik. Kami menunjukkan keberkesanan pendekatan kami melalui ujian pengesahan silang yang meluas pada dataset Oxford Radar RobotCar dan MulRan. Di sini, kami mengatasi pengecaman kedudukan radar terkini yang terkini dan kaedah kesedaran ketidakpastian lain menggunakan hanya satu pertanyaan jiran terdekat. Kami juga menunjukkan peningkatan dalam prestasi dalam persekitaran ujian yang sukar apabila menolak pertanyaan berdasarkan ketidakpastian, sesuatu yang tidak kami perhatikan dengan sistem pengecaman lokasi yang menyedari ketidakpastian bersaing.

Di luar titik permulaan Radar

Pengecaman lokasi dan penyetempatan adalah tugas penting dalam bidang robotik dan sistem autonomi, kerana ia membolehkan sistem memahami dan menavigasi persekitaran mereka. Kaedah pengecaman lokasi berasaskan penglihatan tradisional selalunya terdedah kepada perubahan dalam keadaan persekitaran, seperti pencahayaan, cuaca dan oklusi, mengakibatkan kemerosotan prestasi. Untuk menangani isu ini, terdapat peningkatan minat untuk menggunakan radar FMCW sebagai alternatif penderia yang teguh dalam persekitaran musuh ini.

Kerja sedia ada telah menunjukkan keberkesanan kaedah pengekstrakan ciri buatan tangan dan berasaskan pembelajaran untuk pengecaman kedudukan radar FMCW. Walaupun kejayaan kerja sedia ada, penggunaan kaedah ini dalam aplikasi kritikal keselamatan seperti pemanduan autonomi masih dihadkan oleh anggaran ketidakpastian penentukuran. Dalam bidang ini, perkara berikut perlu dipertimbangkan:

1. Keselamatan memerlukan anggaran ketidakpastian untuk ditentukur dengan baik dengan kadar positif palsu untuk membolehkan penolakan introspektif
2. Pengaturan secara langsung memerlukan Keupayaan inferens berasaskan ketidakpastian imbasan yang pantas
3. Laluan laluan berulang dalam autonomi jangka panjang memerlukan penyelenggaraan peta berterusan dalam talian.

Walaupun VAE lazimnya digunakan untuk tugasan generatif, ruang terpendam kebarangkaliannya boleh berfungsi sebagai perwakilan ruang metrik yang cekap untuk pengecaman lokasi dan membenarkan andaian priori tentang taburan hingar data, yang turut menyediakan anggaran ketidakpastian yang tidak menentu yang dinormalisasi. Oleh itu, dalam kertas kerja ini, untuk mencapai penggunaan radar FMCW yang boleh dipercayai dan selamat dalam pemanduan autonomi, kami menggunakan rangka kerja pembelajaran kontrastif variasi dan mencadangkan kaedah pengenalan kedudukan radar berasaskan ketidakpastian bersatu.

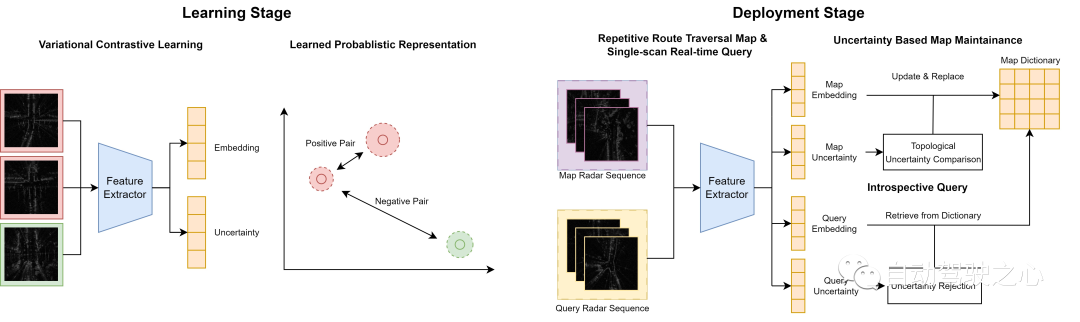
Ikhtisar aliran sistem

Dalam peringkat luar talian, kami menggunakan rangka kerja pembelajaran kontrastif variasi untuk mempelajari ruang benam tersembunyi dengan anggaran ketidakpastian supaya imbasan radar dari lokasi topologi yang serupa adalah berdekatan antara satu sama lain dan begitu juga sebaliknya. Dalam fasa dalam talian, kami membangunkan dua mekanisme berasaskan ketidakpastian untuk mengendalikan imbasan radar yang dikumpulkan secara berterusan untuk inferens dan pembinaan peta. Untuk laluan berulang pada laluan yang sama, kami secara aktif mengekalkan kamus peta bersepadu dengan menggantikan imbasan yang sangat tidak pasti dengan imbasan yang lebih tertentu. Untuk imbasan pertanyaan dengan ketidakpastian yang rendah, kami mendapatkan semula imbasan peta yang sepadan daripada kamus berdasarkan jarak ruang metrik. Sebaliknya, kami menolak ramalan untuk imbasan dengan ketidakpastian yang tinggi.

Pengenalan kepada kaedah Off the Radar

Artikel ini memperkenalkan rangka kerja pembelajaran kontrastif variasi untuk pengecaman kedudukan radar untuk menerangkan ketidakpastian dalam pengecaman kedudukan. Sumbangan utama termasuk:

1. Rangka kerja pembelajaran kontrastif yang menyedari ketidakpastian.
2. Mekanisme pertanyaan introspektif berdasarkan anggaran ketidakpastian penentukuran.
3. Penyelenggaraan peta rekursif dalam talian untuk perubahan persekitaran.

Pembelajaran kontrastif variasi

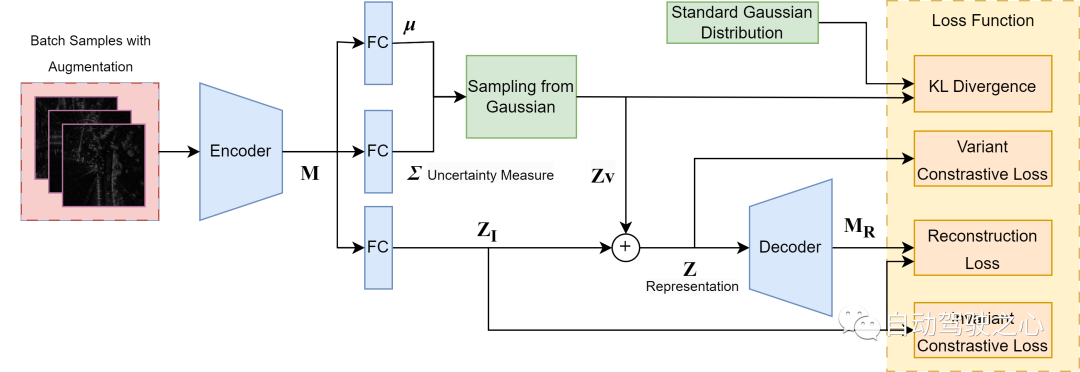
Gambaran keseluruhan rangka kerja pembelajaran kontrastif variasi, berdasarkan [^Lin2018dvml]. parameter untuk model pengenalpastian taburan Gaussian multivariate dengan variansnya sebagai ukuran ketidakpastian. Pembelajaran holistik didorong oleh kedua-dua pembinaan semula dan kerugian kontrastif untuk memastikan perwakilan tersembunyi yang bermaklumat dan diskriminatif bagi imbasan radar.

Kerja dalam bahagian ini merupakan pemboleh utama sumbangan teras kami dan penyepaduan baru pembelajaran metrik variasi mendalam dengan pengecaman kedudukan radar, serta cara baharu untuk mencirikan ketidakpastian dalam pengecaman kedudukan. Seperti yang ditunjukkan dalam rajah, kami mengguna pakai struktur untuk menguraikan pembenaman imbasan radar ke dalam bahagian pemboleh ubah yang disebabkan oleh hingar, yang menangkap varians sumber ketidakpastian yang tidak berkaitan dengan ramalan, dan bahagian invarian semantik untuk gambaran asas. Bahagian pembolehubah kemudiannya diambil sampel daripada taburan Gaussian segi empat sama multivariat terdahulu dan ditambah pada bahagian invarian untuk membentuk perwakilan keseluruhan. Keluaran berubah digunakan secara langsung sebagai ukuran ketidakpastian. Kami menganggap bahawa kami hanya menganggap ketidakpastian yang tidak menentu dalam ramalan model yang disebabkan oleh kekaburan dan rawak yang wujud dalam data sebagai sumber utama ketidakpastian. Terutama untuk imbasan radar, ini mungkin disebabkan oleh bunyi bintik, ketepuan dan oklusi sementara. Kaedah pembelajaran metrik standard, tanpa mengira fungsi kehilangan yang dipilih, cenderung memaksa pemasukan yang sama antara pasangan contoh positif sambil mengabaikan potensi varians antara mereka. Walau bagaimanapun, ini boleh menyebabkan model tidak sensitif terhadap ciri-ciri kecil dan mengatasi pengedaran latihan. Oleh itu, untuk memodelkan varians hingar, kami menggunakan keluaran varians kebarangkalian tambahan dalam struktur untuk menganggarkan ketidakpastian yang tidak menentu. Untuk membina perwakilan radar yang menyedari bunyi seperti itu, kami menggunakan empat fungsi kehilangan untuk membimbing latihan keseluruhan.

1) Kehilangan kontras invarian pada perwakilan deterministik (Z_I) untuk memisahkan hingar tugas-tidak berkaitan daripada semantik radar supaya pembenaman invarian mengandungi maklumat sebab yang mencukupi dan

2) Kehilangan kontras boleh ubah (Z pada keseluruhan kontras; ), wujudkan ruang metrik yang bermakna. Kedua-dua kerugian kontras mengambil bentuk berikut.

Salah satu kelompok terdiri daripada m sampel dan pembesaran bingkai yang dianggarkan secara sementara bagi putaran sintetik menggunakan strategi "putaran", iaitu hanya penambahan putaran, untuk invarian putaran. Matlamat kami adalah untuk memaksimumkan kebarangkalian bahawa sampel tambahan diiktiraf sebagai contoh asal, sambil meminimumkan kebarangkalian kes pembalikan.

di mana pembenaman ( Z ) ialah ( Z_I ) atau ( Z ) seperti yang diterangkan dalam persamaan 1) dan 2).

3) Perbezaan Kullback–Leibler (KL) Antara taburan Gaussian yang dipelajari dan taburan Gaussian multivariat isotropik standard, ini ialah andaian apriori kami tentang hingar data. Ini memastikan pengedaran hingar yang sama merentas semua sampel dan menyediakan rujukan statik untuk nilai mutlak keluaran pembolehubah.

4) Kehilangan pembinaan semula adalah antara peta ciri yang diekstrak (M) dan output penyahkod (M_R), yang memaksa perwakilan keseluruhan (Z) mengandungi maklumat yang mencukupi daripada imbasan radar asal untuk dibina semula. Walau bagaimanapun, kami hanya membina semula peta ciri berdimensi lebih rendah dan bukannya pembinaan semula imbasan radar peringkat piksel untuk mengurangkan kos pengiraan dalam proses penyahkodan.

Walaupun struktur VAE biasa yang hanya didorong oleh perbezaan KL dan kehilangan pembinaan semula juga memberikan varians terpendam, ia dianggap tidak boleh dipercayai untuk anggaran ketidakpastian disebabkan oleh keruntuhan posterior yang terkenal dan masalah varians yang hilang. Ketidakberkesanan ini disebabkan terutamanya oleh ketidakseimbangan kedua-dua kerugian semasa latihan: apabila perbezaan KL mendominasi, ruang terpendam posterior dipaksa untuk menyamai sebelumnya, manakala apabila kerugian pembinaan semula menguasai, varians terpendam ditolak kepada sifar. Walau bagaimanapun, dalam pendekatan kami, kami mencapai latihan yang lebih stabil dengan memperkenalkan kehilangan kontrastif berubah-ubah sebagai penyelaras tambahan, di mana varians didorong untuk mengekalkan sempadan yang teguh antara pusat kluster dalam ruang metrik. Hasilnya, kami memperoleh varians spatial asas yang lebih dipercayai yang mencerminkan ketidakpastian asas dalam persepsi radar. Kami memilih untuk menunjukkan faedah pendekatan khusus kami untuk mempelajari ketidakpastian dalam tetapan kehilangan ciri yang semakin meningkat. Dalam bidang ini, teknik terkini untuk pengecaman kedudukan radar sudah menggunakan kerugian dengan banyak (iaitu, lebih daripada 2) sampel negatif, jadi kami melanjutkan berdasarkan ini.

Penyelenggaraan peta berterusan

Penyelenggaraan peta berterusan ialah ciri penting sistem dalam talian, kerana kami berhasrat untuk menggunakan sepenuhnya data imbasan yang diperoleh semasa operasi kenderaan autonomi dan menambah baik peta secara rekursif. Proses penggabungan imbasan radar baharu ke dalam peta induk yang terdiri daripada imbasan yang dilalui sebelum ini adalah seperti berikut. Setiap imbasan radar diwakili oleh perwakilan tersembunyi dan metrik ketidakpastian. Semasa proses penggabungan, kami mencari sampel positif yang sepadan untuk setiap imbasan baharu dengan jarak topologi di bawah ambang. Jika imbasan baharu mempunyai ketidakpastian yang lebih rendah maka ia disepadukan ke dalam peta induk dan menggantikan imbasan padanan, jika tidak, ia akan dibuang.

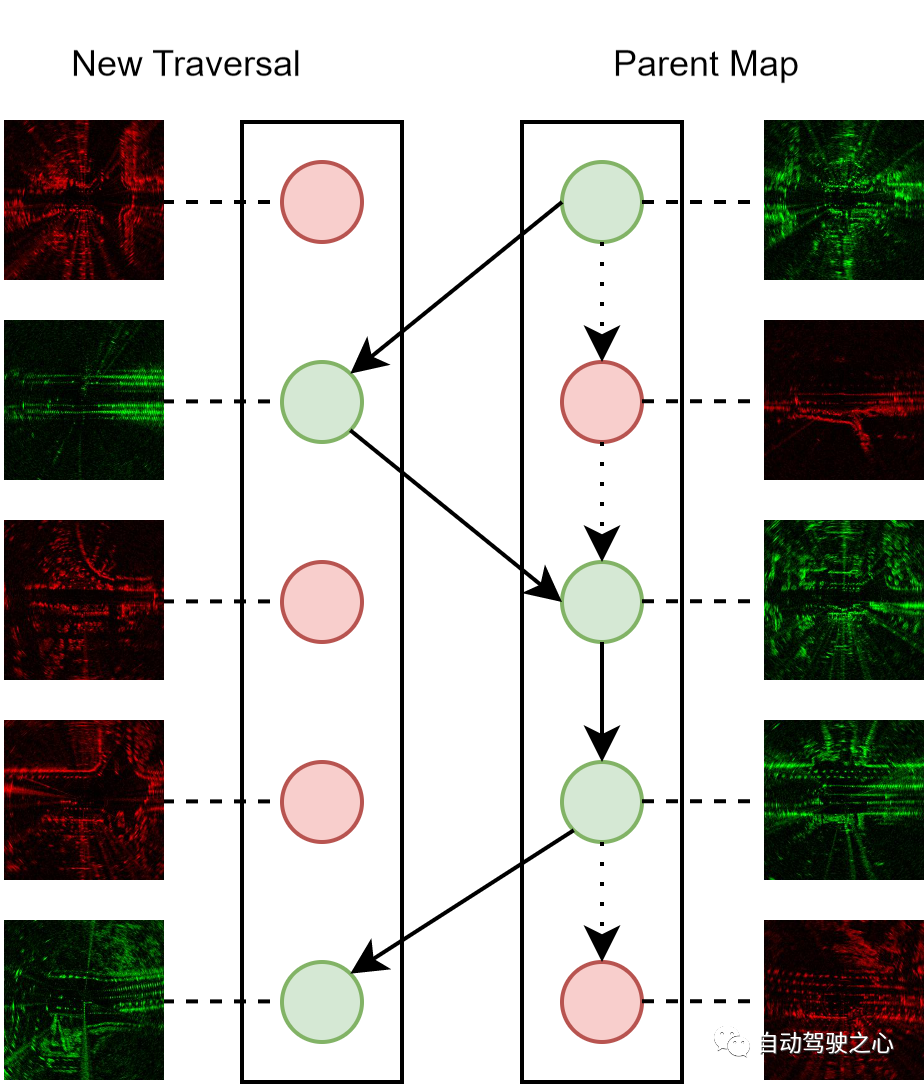
Gambarajah skematik penyelenggaraan peta: nod merah dan hijau mewakili imbasan radar dengan ketidakpastian yang lebih tinggi dan lebih rendah masing-masing. Kami sentiasa mengekalkan peta induk sebagai rujukan kedudukan untuk setiap lokasi, hanya terdiri daripada imbasan dengan ketidakpastian yang paling rendah. Ambil perhatian bahawa tepi putus-putus mewakili keadaan awal peta induk, dan tepi pepejal mewakili versi peta induk yang dikemas kini.

Dengan melakukan proses penyelenggaraan secara berulang, kami boleh meningkatkan kualiti peta induk bersepadu secara beransur-ansur. Oleh itu, algoritma penyelenggaraan boleh berfungsi sebagai strategi penggunaan dalam talian yang berkesan kerana ia secara berterusan mengeksploitasi pelbagai pengalaman melalui laluan yang sama untuk meningkatkan prestasi pengecaman sambil mengekalkan saiz peta induk yang tetap, menghasilkan kos pengiraan dan penyimpanan yang dianggarkan.

Pertanyaan Introspektif

Disebabkan ketidakpastian model dengan ukuran daripada taburan Gaussian standard, varians anggaran adalah hampir 1 untuk semua dimensi. Oleh itu, kita boleh menentukan sepenuhnya skala dan resolusi penolakan ketidakpastian menggunakan dua hiperparameter, Delta dan N. Ambang T yang terhasil ditakrifkan seperti berikut:

Memandangkan imbasan dengan varians pendam m-dimensi, kami purata ke atas semua dimensi, menghasilkan ukuran ketidakpastian skalar

Penolakan ramalan

Pada masa penolakan inferens, kami melakukan introspeksi inferens. , imbasan pertanyaan di mana varians melebihi ambang yang ditentukan akan ditolak untuk dikenal pasti. Kaedah sedia ada, seperti STUN dan MC Dropout, membahagikan julat ketidakpastian kumpulan sampel kepada tahap ambang secara dinamik. Walau bagaimanapun, ini memerlukan berbilang sampel semasa inferens dan boleh menyebabkan prestasi penolakan yang tidak stabil, terutamanya apabila terdapat hanya sebilangan kecil sampel. Sebaliknya, strategi ambang statik kami menyediakan tahap ambang bebas sampel dan menyediakan anggaran ketidakpastian imbasan tunggal yang konsisten dan penolakan. Ciri ini penting untuk penggunaan masa nyata sistem pengecaman lokasi, kerana imbasan radar diperoleh bingkai demi bingkai semasa memandu.

Butiran eksperimen

Artikel ini menggunakan dua set data: 1) Oxford Radar RobotCar dan 2) MulRan. Kedua-dua set data menggunakan radar pengimbasan CTS350-X Navtech FMCW. Sistem radar beroperasi dalam julat 76 GHz hingga 77 GHz dan boleh menjana sehingga 3768 bacaan julat dengan resolusi 4.38 cm. Prestasi pengiktirafan

penanda aras dilakukan dengan membandingkan dengan beberapa kaedah sedia ada, termasuk VAE asal, kaedah pengenalan tapak radar tercanggih yang dicadangkan oleh Gaddet al dipanggil BCRadar ) , dan kaedah berasaskan bukan pembelajaran RingKey (sebahagian daripada ScanContext, tanpa pemurnian putaran). Selain itu, prestasi dibandingkan dengan MC Dropout dan STUN, yang berfungsi sebagai garis dasar untuk pengecaman tempat yang tidak pasti.

Kajian AblasiUntuk menilai keberkesanan modul pertanyaan introspektif (Q) dan penyenggaraan peta (M) kami yang dicadangkan, kami melakukan kajian ablasi dengan membandingkan pelbagai varian kaedah kami, masing-masing dilambangkan sebagai OURS(O/M) /Q /QM), butirannya adalah seperti berikut:

1. O: Tiada penyelenggaraan peta, tiada pertanyaan introspeksi
2. M: Hanya penyelenggaraan peta
3. S: Hanya pertanyaan introspeksi
4. QM: Kedua-dua penyelenggaraan peta dan pertanyaan introspeksi adalah khusus Untuk , kami membandingkan prestasi pengenalpastian antara O dan M, dan prestasi anggaran ketidakpastian antara Q dan QM.

Tetapan BiasaUntuk memastikan perbandingan yang adil, kami mengguna pakai kerugian kontrastif kelompok biasa untuk semua kaedah berasaskan pembelajaran kontras, menghasilkan fungsi kerugian yang konsisten merentas penanda aras.

Butiran pelaksanaan

Persediaan imbasan
Untuk semua kaedah, kami menukar imbasan radar kutub dengan galas A = 400 dan B = 3768 grid ke dalam imbasan Cartesian, dengan setiap kotak bersaiz 4.38 cm, dengan W 25 = panjang sisi dan saiz kotak 0.5 m.

Melatih hiperparameter
Kami menggunakan VGG-19 [^simonyan2014sangat^] sebagai pengekstrak ciri latar belakang dan menggunakan lapisan linear untuk menayangkan ciri yang diekstrak ke dimensi benam yang lebih rendah d=128. Kami melatih semua garis dasar untuk 10 zaman dalam Oxford Radar RobotCar dan 15 lelaran dalam MulRan dengan kadar pembelajaran 1e{-5} dan saiz kelompok 8.

Metrik Penilaian

Untuk menilai prestasi pengecaman tempat, kami menggunakan Recall@N (R@N)Recall@N (R@N) 指标，这是通过确定在 N 个候选者中是否至少有一个候选者接近 GPS/INS 所指示的地面真实值来确定的本地化的准确性。这对于自动驾驶应用中的安全保证尤为重要，因为它反映了系统对假阴性率的校准。我们还使用 Average Precision (AP) 来测量所有召回级别的平均精度。最后，我们使用 F-scores 与 beta=2/1/0.5 来分配召回对精确度的重要性级别，作为评估整体识别性能的综合指标。

此外，为了评估不确定性估计性能。我们使用 Recall@RR，在这里我们执行内省查询拒绝，并在不同的不确定性阈值级别上评估 Recall@N=1 -- 拒绝所有查询的扫描的不确定性大于阈值的。我们因此拒绝了 0-100% 的查询。

结果总结

地点识别性能

如 Oxford Radar RobotCar实验中表格1所示，我们的方法仅使用度量学习模块，在所有指标上都取得了最高的性能。具体来说，在 Recall@1 方面，我们的方法 OURS(O) 展示了通过变分对比学习框架学习的方差解耦表示的有效性，实现了超过 90.46% 的识别性能。这进一步得到了 MulRan 实验结果的支持，如表2所示，我们的方法在 Recall@1、总体 F-scores 和 AP 上均优于其他所有方法。尽管在 MulRan 实验中，VAE 在 Recall@5/10 上优于我们的方法，但我们的方法在两种设置中的最佳 F-1/0.5/2 和 AP Penunjuk, iaitu dengan menentukan sama ada terdapat sekurang-kurangnya seorang calon di kalangan N calon Ketepatan penyetempatan ditentukan dengan mendekati kebenaran asas yang ditunjukkan oleh GPS/INS. Ini amat penting untuk jaminan keselamatan dalam aplikasi pemanduan autonomi, kerana ia mencerminkan penentukuran kadar negatif palsu sistem. Kami juga menggunakan

Ketepatan Purata (AP)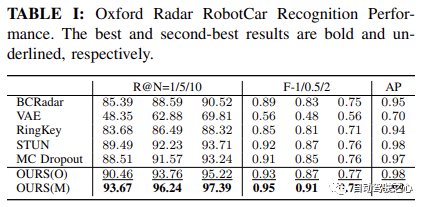

untuk mengukur ketepatan purata semua peringkat ingatan semula. Akhir sekali, kami menggunakan

F-skor dan

beta=2/1/0.5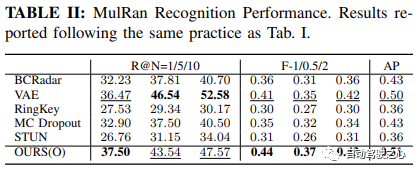

untuk menetapkan tahap kepentingan ingatan kepada ketepatan sebagai ukuran prestasi pengecaman keseluruhan penunjuk.

Selain itu, untuk menilai prestasi anggaran ketidakpastian. Kami menggunakan 🎜 🎜Recall@RR, di mana kami melakukan penolakan pertanyaan introspektif dan menilai pada tahap ambang ketidakpastian yang berbeza 🎜 🎜Recall@1, keseluruhan 🎜 🎜F-skor🎜 🎜 dan 🎜 🎜F- 1/0.5/2🎜 🎜 dan 🎜 🎜Recall@1 进一步提高到 93.67%，超过了当前最先进的方法 STUN，超出了 4.18%。这进一步证明了学习方差作为一个有效的不确定性度量，以及基于不确定性的地图集成策略在提高地点识别性能方面的有效性。

不确定性估计性能

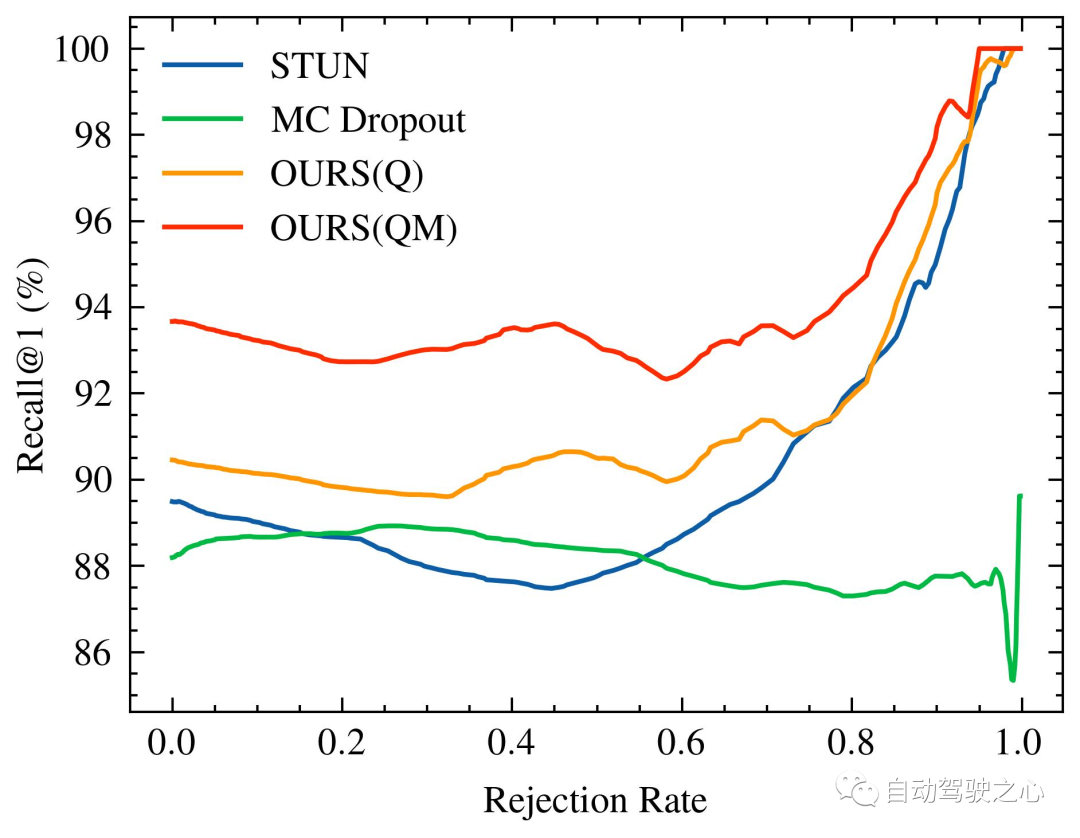
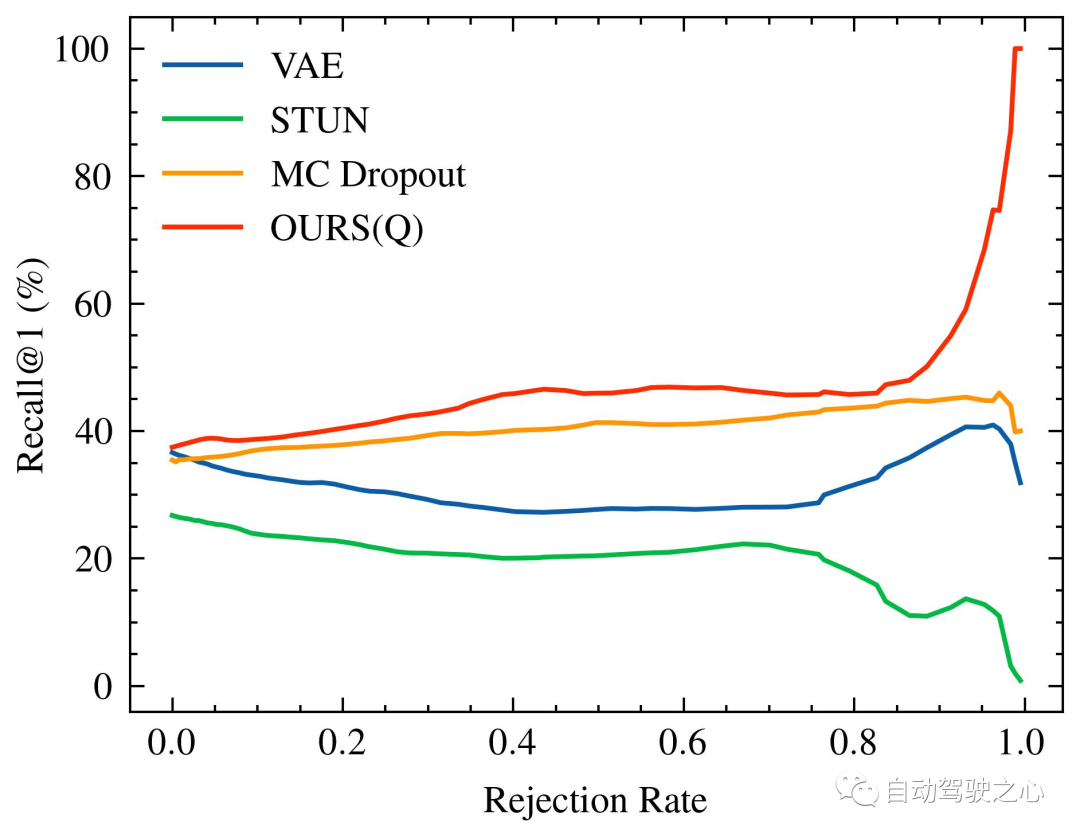
随着被拒绝的不确定查询的百分比增加，识别性能的变化，特别是 Recall@1，在 Oxford Radar RobotCar 实验中如图1所示，在 MulRan 实验中如图2所示。值得注意的是，我们的方法是唯一一个在两种实验设置中都展示出随着不确定查询拒绝率增加而持续改进的识别性能的方法。在MulRan实验中，OURS(Q) 是唯一一个随着拒绝率增加而持续平稳地提高 Recall@RR 指标的方法。与 VAE 和 STUN 相比，这两种方法也像我们的方法一样估计了模型的不确定性，OURS(Q) 在 Recall@RR=0.1/0.2/0.5 上实现了 +(1.32/3.02/8.46)% 的改进，而 VAE 和 STUN 分别下降了 -(3.79/5.24/8.80)% 和 -(2.97/4.16/6.30)%。

Oxford Radar RobotCar的内省查询拒绝性能。随着被拒绝的不确定查询的百分比增加，Recall@1增加/减少。由于 VAE 的性能与其他方法相比较低（具体为Recall@RR=0.1/0.2/0.5的 (48.42/48.08/18.48)%），因此没有进行可视化。

Mulran的内省查询拒绝性能。格式同上。

另一方面，与 MC Dropout 相比，后者估计了由于数据偏见和模型误差导致的认知不确定性，尽管它在Oxford Radar RobotCar实验的早期阶段有更高的 Recall@1 增加，但其性能总体上低于我们的，并且随着拒绝率进一步增加，未能实现更大的改进。最后，比较 OURS(Q) 和 OURS(QM) 在Oxford Radar RobotCar实验中，我们观察到 Recall@RR dipertingkatkan lagi kepada 93.67%, melebihi kaedah terkini STUN oleh 4.18%. Ini seterusnya menunjukkan keberkesanan varians yang dipelajari sebagai ukuran ketidakpastian yang berkesan dan strategi penyepaduan peta berasaskan ketidakpastian dalam meningkatkan prestasi pengecaman tempat.

Prestasi anggaran ketidakpastian

Perubahan dalam prestasi pengecaman apabila peratusan pertanyaan tidak pasti yang ditolak meningkat, terutamanya

🎜<code style=" background-color: rgb padding: border-radius: overflow-wrap: break-word text-indent: display: inline-block>Recall@RR=0.1/0.2/0.5🎜 🎜dilaksanakan pada Terdapat peningkatan sebanyak +(1.32/ 3.02/8.46)%, manakala VAE dan STUN menurun masing-masing sebanyak -(3.79/5.24/8.80)% dan -(2.97/4.16/6.30). 🎜🎜🎜 Prestasi penolakan pertanyaan introspeksi Oxford Radar RobotCar. Apabila peratusan pertanyaan tak tentu yang ditolak meningkat, Recall@1naik/turun. Disebabkan oleh prestasi VAE yang rendah berbanding dengan kaedah lain (khususnya Recall@RR=0.1/0.2/0.5's (48.42/48.08/18.48)%), jadi ia tidak digambarkan. 🎜🎜🎜 Prestasi penolakan pertanyaan introspektif Mulran. Formatnya sama seperti di atas. 🎜🎜Sebaliknya, berbanding MC Dropout, yang menganggarkan ketidakpastian epistemik akibat bias data dan ralat model, walaupun ia mempunyai 🎜 yang lebih tinggi pada peringkat awal eksperimen Oxford Radar RobotCar 🎜Visualisasi imbasan radar dengan tahap ketidakpastian yang berbeza. Empat contoh di sebelah kiri adalah daripada Oxford Radar RobotCar Dataset, manakala empat contoh di sebelah kanan adalah daripada MulRan. Kami menunjukkan 10 sampel teratas dengan ketidakpastian tertinggi (atas) / terendah (bawah). Imbasan radar dipaparkan dalam koordinat Cartesan untuk kontras yang dipertingkatkan. Histogram di bawah setiap imej menunjukkan ciri deskriptor RingKey bagi keamatan yang diekstrak daripada semua sudut azimut. <p>Ini seterusnya menyokong hipotesis kami tentang sumber ketidakpastian dalam persepsi radar dan berfungsi sebagai bukti kualitatif bahawa pengukuran ketidakpastian kami menangkap bunyi data ini. </p> <h4><span>Perbezaan Set Data</span></h4> <p>Dalam percubaan penanda aras kami, kami melihat perbezaan yang ketara dalam prestasi pengecaman antara kedua-dua set data. Kami fikir saiz data latihan yang tersedia mungkin merupakan sebab yang sah. Set latihan Oxford Radar RobotCar merangkumi lebih daripada 300Km pengalaman memandu, manakala set data MulRan hanya merangkumi kira-kira 120Km. Walau bagaimanapun, juga mengambil kira kemerosotan prestasi kaedah deskriptor RingKey. Ini menunjukkan bahawa mungkin terdapat ciri yang tidak dapat dibezakan dalam persepsi pemandangan radar. Sebagai contoh, kami mendapati bahawa persekitaran dengan kawasan terbuka yang jarang sering menghasilkan imbasan yang sama dan prestasi pengecaman suboptimum. Kami menunjukkan pada set data ini perkara yang berlaku kepada sistem kami dan pelbagai garis dasar di bawah situasi ketidakpastian tinggi ini. </p> <p style="text-align:center;"><img src="https://img.php.cn/upload/article/000/465/014/169828998861545.jpg" alt="Cara melaksanakan pengecaman kedudukan radar FMCW secara elegan (IROS2023)"></p> <p>Pautan asal: https://mp.weixin.qq.com/s/wu7whicFEAuo65kYp4quow</p>

Atas ialah kandungan terperinci Cara melaksanakan pengecaman kedudukan radar FMCW secara elegan (IROS2023). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!