Rumah >Peranti teknologi >AI >Cerapan tentang pendaraban matriks daripada perspektif 3D, beginilah rupa pemikiran AI
Cerapan tentang pendaraban matriks daripada perspektif 3D, beginilah rupa pemikiran AI
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-10-16 08:09:01991semak imbas
Jika proses pelaksanaan pendaraban matriks boleh dipaparkan dalam 3D, tidaklah begitu sukar untuk mempelajari pendaraban matriks ketika itu.
Kini, pendaraban matriks telah menjadi bahan binaan model pembelajaran mesin dan asas kepada pelbagai teknologi AI yang berkuasa Memahami kaedah pelaksanaannya pasti akan membantu kita memahami AI ini dan dunia yang semakin pintar ini dengan lebih mendalam.
Artikel dari blog PyTorch ini akan memperkenalkan mm, alat visualisasi untuk pendaraban matriks dan gabungan pendaraban matriks.
Oleh kerana mm menggunakan ketiga-tiga dimensi spatial, berbanding carta dua dimensi biasa, mm membantu untuk memaparkan dan merangsang idea secara intuitif, dan menggunakan kurang overhed kognitif, terutamanya (tetapi tidak terhad kepada) ) untuk orang yang mahir dalam visual dan spatial berfikir.
Dan dengan tiga dimensi untuk menggabungkan pendaraban matriks, ditambah dengan keupayaan untuk memuatkan pemberat terlatih, mm boleh memvisualisasikan ungkapan kompaun besar (seperti kepala perhatian) dan memerhati corak tingkah laku sebenar mereka.
mm adalah interaktif sepenuhnya, berjalan dalam iframe penyemak imbas atau buku nota, dan ia menyimpan keadaan penuh dalam URL, jadi pautan adalah sesi yang boleh dikongsi (tangkapan skrin dan video dalam artikel ini mempunyai pautan, tersedia di Buka visualisasi yang sepadan dalam alat ini, sila rujuk blog asal untuk butiran). Panduan rujukan ini menerangkan semua ciri yang tersedia.
Alamat alat: https://bhosmer.github.io/mm/ref.html
Teks blog asal: https://pytorch.org/blog/inside-the-matrix
Ini artikel adalah yang pertama saya akan memperkenalkan kaedah visualisasi, membina gerak hati dengan menggambarkan beberapa pendaraban dan ungkapan matriks mudah, dan kemudian menyelami beberapa contoh lanjutan:
Pengenalan: Mengapa visualisasi ini lebih baik? . Struktur NanoGPT, nilai dan gelagat pengiraan sepasang kepala perhatian untuk GPT-2
Perhatian Parallelizing: Visualisasikan penyejajaran kepala perhatian menggunakan contoh daripada kertas Blockwise Parallel Transformer baru-baru ini.
Saiz lapisan perhatian: Apabila kita memvisualisasikan keseluruhan lapisan perhatian sebagai satu struktur, apakah rupa separuh MHA dan separuh FFA lapisan perhatian bersama-sama? Bagaimanakah imej berubah semasa proses penyahkodan autoregresif?
LoRA: Penjelasan visual terperinci tentang seni bina kepala perhatian ini
- 1 Pengenalan Pendekatan visualisasi
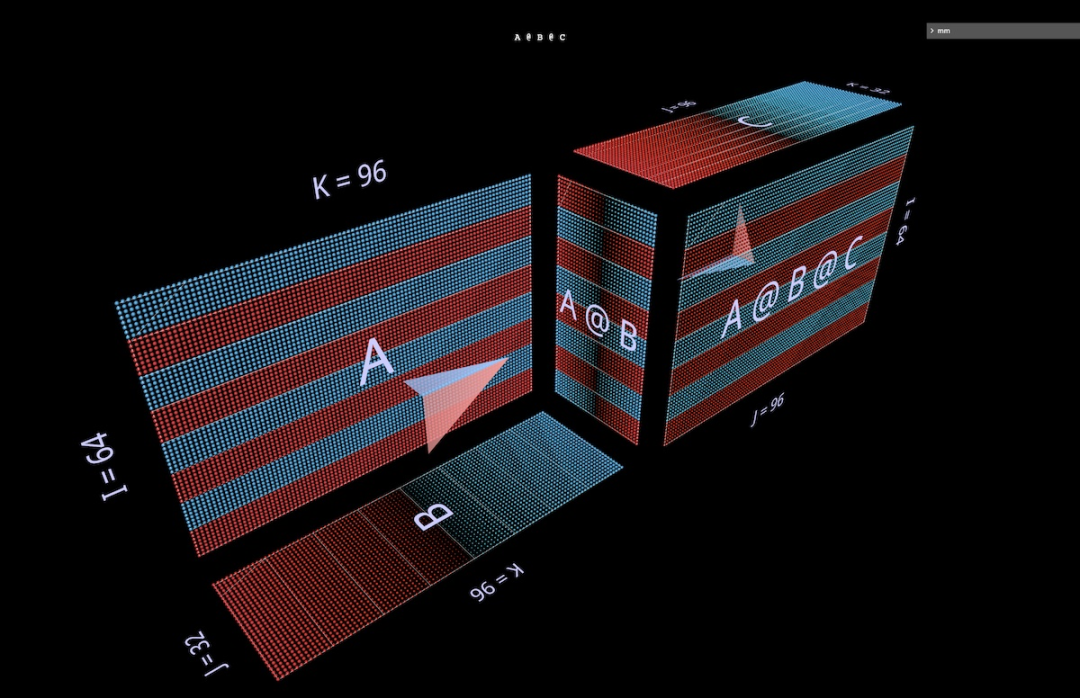
mm adalah berdasarkan premis bahawa pendaraban matriks pada asasnya adalah operasi tiga dimensi.
Dalam erti kata lain:
Apabila kita membalut pendaraban matriks dalam kubus dengan cara ini, antara bentuk parameter, bentuk hasil dan dimensi yang dikongsi Hubungan yang betul semua ada di tempatnya.
Kini pengiraan pendaraban matriks masuk akal geometri: setiap kedudukan i, j dalam matriks yang terhasil menambat vektor yang berjalan di sepanjang dimensi kedalaman k di dalam kubus, yang memanjang dari baris ke-i L Satah mendatar memotong menegak satah memanjang dari lajur ke-j R. Di sepanjang vektor ini, pasangan unsur (i, k) (k, j) daripada hujah kiri dan kanan bertemu dan didarab, dan hasil darab yang terhasil dijumlahkan bersama k dan diletakkan ke dalam i hasil, kedudukan j.
Ini ialah makna intuitif bagi pendaraban matriks: 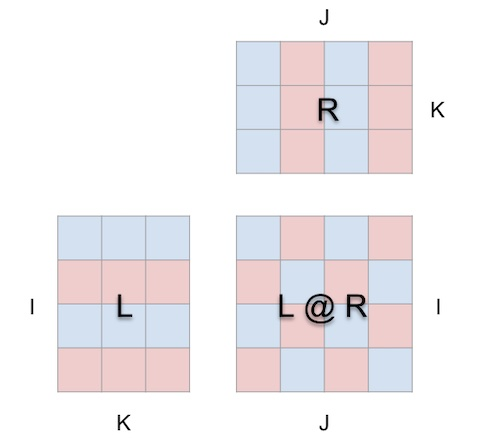
 Untuk arah, alat memaparkan anak panah di dalam kubus yang menunjuk kepada matriks hasil, dengan fletching biru dari parameter kiri dan fletching merah dari parameter kanan. Alat ini juga memaparkan garis penunjuk putih untuk menunjukkan paksi baris setiap matriks, walaupun garisan ini kabur dalam tangkapan skrin ini.
Untuk arah, alat memaparkan anak panah di dalam kubus yang menunjuk kepada matriks hasil, dengan fletching biru dari parameter kiri dan fletching merah dari parameter kanan. Alat ini juga memaparkan garis penunjuk putih untuk menunjukkan paksi baris setiap matriks, walaupun garisan ini kabur dalam tangkapan skrin ini.
Kekangan susun atur adalah mudah dan mudah:
Parameter dan hasil sebelah kiri mesti bersebelahan di sepanjang dimensi ketinggian (i) dikongsi
Parameter dan hasil sebelah kanan mesti bersebelahan dengan lebar yang dikongsi bersamanya (j) dimensi
Parameter kiri dan kanan mestilah bersebelahan di sepanjang dimensi kongsi (lebar kiri / ketinggian kanan), yang menjadi dimensi kedalaman (k) pendaraban matriks
- Perwakilan geometri ini boleh digunakan untuk memvisualisasikan semua pemfaktoran pendaraban matriks Standard menyediakan asas yang kukuh dan asas intuitif untuk meneroka gabungan bukan remeh pendaraban matriks kompleks, seperti yang akan kita lihat seterusnya.
- 2 Memanaskan Badan: Animasi
Sebelum menyelami contoh yang lebih kompleks, mari kita lihat rupa gaya visualisasi ini untuk membina pemahaman intuitif tentang alat tersebut.
- 2a dot produk
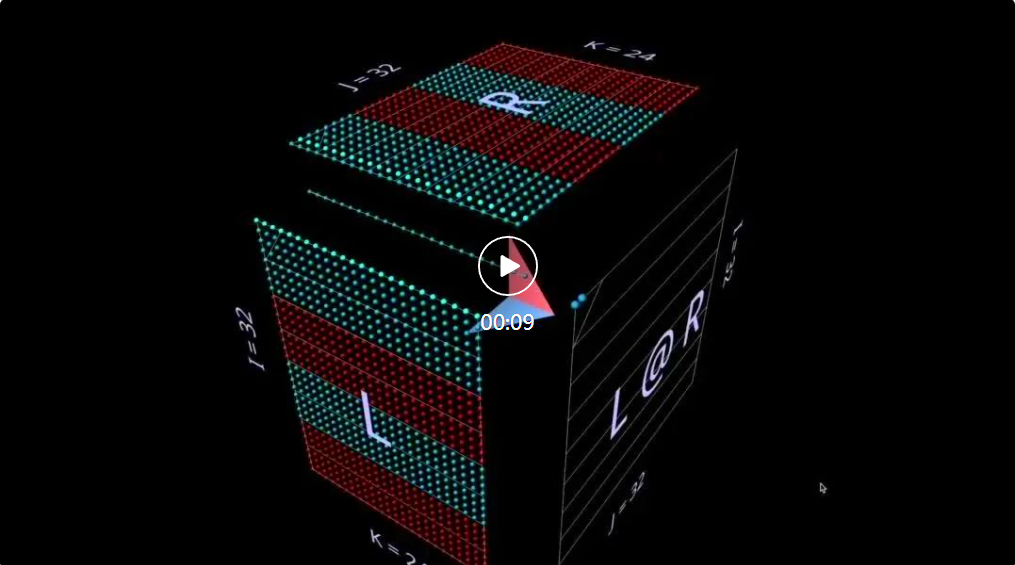
Mula-mula, mari lihat algoritma klasik - kira setiap elemen hasil dengan mengira hasil darab titik baris kiri dan lajur kanan yang sepadan. Seperti yang anda boleh lihat daripada animasi di sini, vektor nilai berganda menyapu ke bahagian dalam kubus, setiap kali menyampaikan hasil penjumlahan di lokasi yang sepadan.
Di sini, L mempunyai blok baris yang diisi dengan 1 (biru) atau -1 (merah); R mempunyai blok lajur yang diisi dengan sama. Di sini k ialah 24, jadi matriks yang terhasil (L @ R) mempunyai nilai biru 24 dan nilai merah -24.

2b Produk matriks-vektor
terurai menjadi hasil matriks-vektor Pendaraban matriks kelihatan seperti satah menegak (hasil darab setiap lajur parameter kiri dan parameter kanan) kerana ia mendatar merentasi bahagian dalam kubus , plot lajur pada hasil:

Adalah menarik untuk memerhatikan nilai perantaraan penguraian, walaupun contohnya mudah.
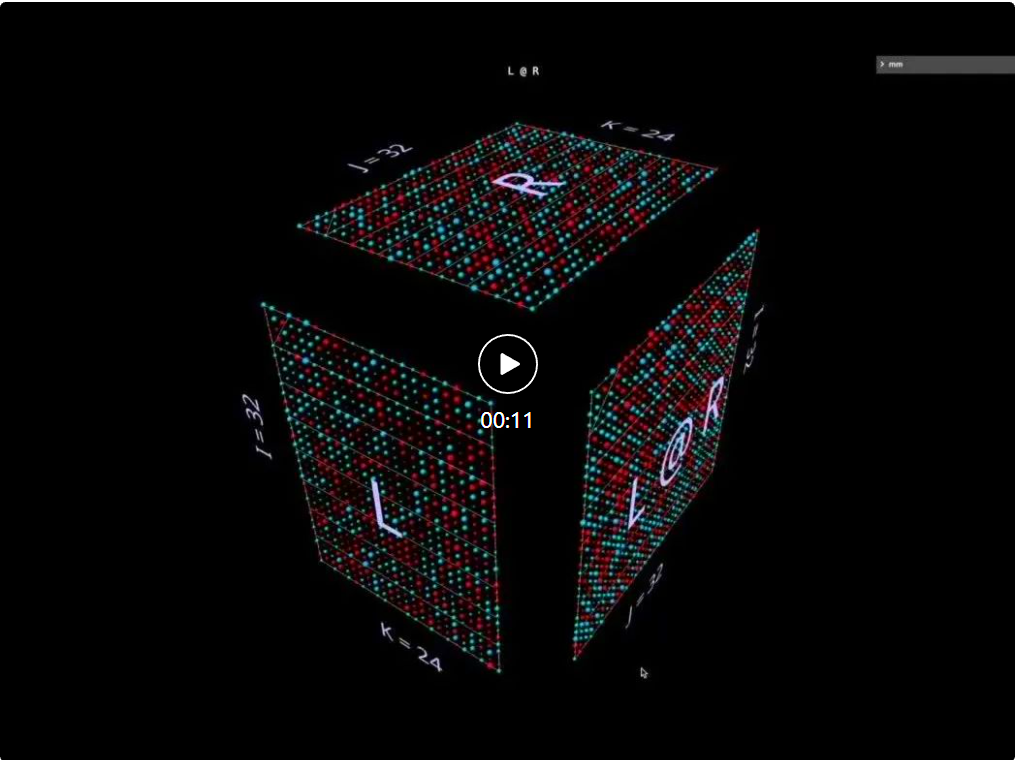
Sebagai contoh, perhatikan corak menegak yang menonjol produk vektor matriks di tengah apabila kita menggunakan parameter yang dimulakan secara rawak - ini mencerminkan fakta bahawa setiap nilai perantaraan ialah salinan berskala lajur bagi parameter sebelah kiri:

2c Vektor - Produk matriks
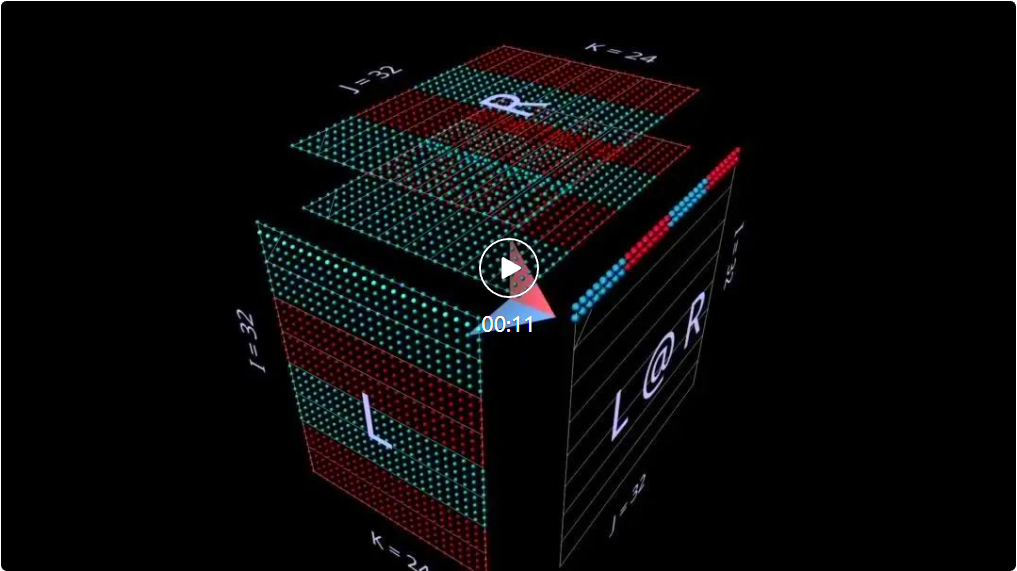
terurai menjadi vektor - Pendaraban matriks produk matriks kelihatan seperti satah mendatar yang menarik baris ke hasil apabila ia melepasi bahagian dalam kubus:
 witching
witchingkepada parameter yang dimulakan secara rawak, anda boleh melihat corak yang serupa dengan produk matriks-vektor - hanya kali ini dalam mod mendatar, sepadan dengan fakta bahawa setiap produk vektor-matriks perantaraan ialah salinan berskala baris bagi parameter sebelah kanan.
Apabila memikirkan tentang cara pendaraban matriks mewakili struktur jumlah pangkat parameternya, pendekatan yang berguna ialah membayangkan kedua-dua mod ini berlaku serentak dalam pengiraan:
 Ini satu lagi yang menggunakan produk vektor-matriks untuk membina intuisi Contoh, yang menunjukkan bahawa matriks identiti bertindak seperti cermin yang diletakkan pada sudut 45 darjah, mencerminkan parameter dan keputusan yang sepadan:
Ini satu lagi yang menggunakan produk vektor-matriks untuk membina intuisi Contoh, yang menunjukkan bahawa matriks identiti bertindak seperti cermin yang diletakkan pada sudut 45 darjah, mencerminkan parameter dan keputusan yang sepadan: 
2d Menjumlahkan produk luar
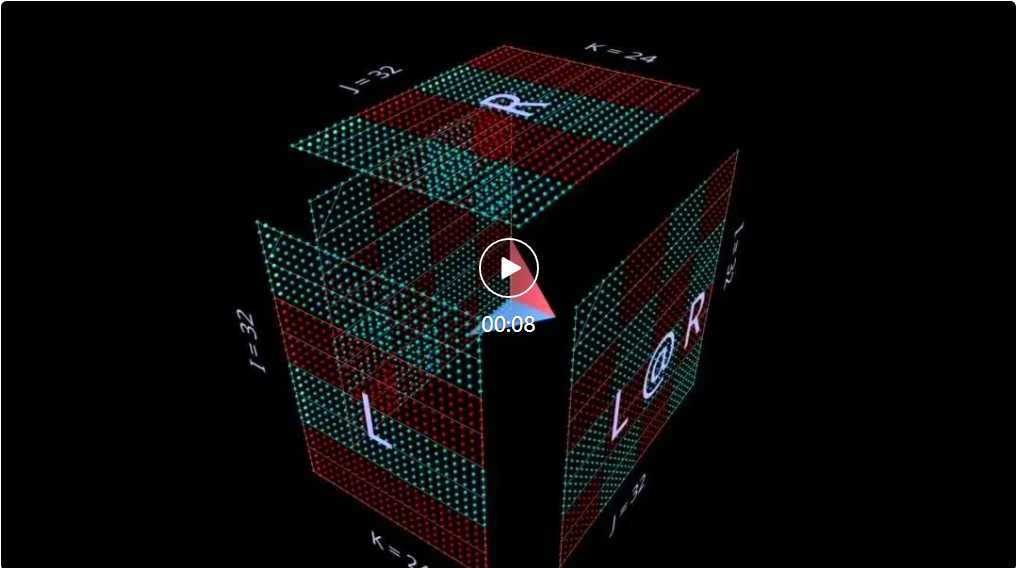
Penguraian satah ketiga ialah Sepanjang paksi-k, keputusan pendaraban matriks dikira dengan menjumlahkan hasil keluaran luar vektor. Di sini kita dapat melihat bahawa satah produk luar menyapu kiub "dari belakang ke hadapan", terkumpul ke dalam hasil:

Menggunakan matriks yang dimulakan secara rawak untuk penguraian ini, kita bukan sahaja dapat melihat nilai, tetapi juga hasilnya. Peringkat terkumpul apabila setiap hasil keluaran luar peringkat 1 ditambah kepadanya.
Ini juga menerangkan secara intuitif mengapa "pemfaktoran peringkat rendah" (iaitu, menganggarkan matriks dengan membina pendaraban matriks dengan parameter yang lebih kecil dalam dimensi kedalaman) berfungsi paling baik apabila matriks yang dianggarkan ialah matriks peringkat rendah. Inilah LoRA yang akan disebut kemudian:

3 Memanaskan Badan: Ungkapan
Bagaimanakah cara kita boleh melanjutkan kaedah visualisasi ini kepada penguraian pendaraban matriks? Contoh sebelumnya menggambarkan pendaraban matriks tunggal L @ R matriks L dan R, tetapi bagaimana jika L dan/atau R adalah pendaraban matriks sendiri?
Ternyata pendekatan ini berskala baik untuk ungkapan majmuk. Peraturan utama adalah mudah: pendaraban subungkapan (sub)matriks ialah satu lagi kubus tertakluk kepada kekangan susun atur yang sama seperti pendaraban matriks induk, muka hasil pendaraban submatriks juga merupakan muka parameter pendaraban matriks induk, sama seperti kovalen; Elektron yang dikongsi.
Dalam kekangan ini, kita boleh mengatur pelbagai aspek pendaraban submatriks mengikut keperluan kita sendiri. Skim lalai alat digunakan di sini, yang menghasilkan kiub cembung dan cekung berselang-seli - susun atur ini berfungsi dengan baik dalam amalan, memaksimumkan ruang sambil meminimumkan oklusi. (Tetapi reka letak boleh disesuaikan sepenuhnya, lihat halaman alat mm untuk mendapatkan butiran.)
Bahagian ini akan menggambarkan beberapa blok binaan utama model pembelajaran mesin supaya pembaca boleh membiasakan diri dengan perwakilan visual ini dan mendapat intuisi baharu daripadanya.
3a Ungkapan Bersekutu Kiri
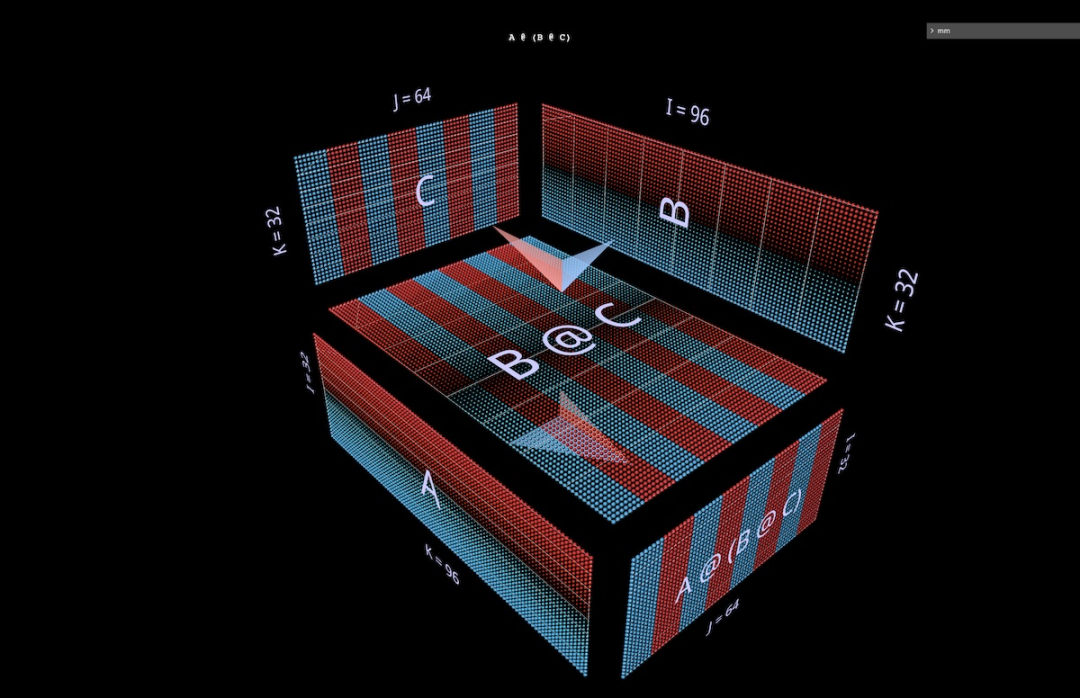
Dua ungkapan bentuk (A @ B) @ C akan diperkenalkan di bawah, setiap satu dengan bentuk dan ciri uniknya sendiri. (Nota: mm mengikut konvensyen bahawa pendaraban matriks dibiarkan bersekutu, jadi (A @ B) @ C boleh ditulis sebagai A @ B @ C.)
Mula-mula berikan A @ B @ C bentuk FFN yang sangat tersendiri, di mana "Dimensi tersembunyi" lebih luas daripada dimensi "input" atau "output". (Khususnya, untuk contoh ini, ini bermakna bahawa lebar B adalah lebih besar daripada lebar A atau C.)
Seperti contoh pendaraban matriks tunggal, anak panah terapung menghala ke matriks yang terhasil, di mana fletching biru berasal dari hujah kiri , fletching merah datang daripada parameter di sebelah kanan.

Dan apabila lebar B lebih kecil daripada lebar A atau C, akan ada kesesakan dalam visualisasi A @ B @ C, serupa dengan bentuk pengekod auto.

Corak modul bonggol berselang-seli juga boleh dilanjutkan kepada rantaian panjang sewenang-wenangnya: Sebagai contoh, kesesakan berbilang lapisan ini:

3b Ungkapan bersekutu kanan
Visualisasi kanan seterusnya @ ( B @ C). Serupa dengan pengembangan mendatar ungkapan bersekutu kiri - boleh dikatakan bermula dari parameter kiri ungkapan akar, rantai ungkapan bersekutu kanan dikembangkan secara menegak, bermula dari parameter kanan ungkapan akar. Seseorang kadangkala boleh melihat MLP terbentuk dalam bentuk gabungan kanan, di mana sebelah kanan ialah input kolumnar dan lapisan berat berjalan dari kanan ke kiri. Menggunakan matriks contoh FFN dua lapisan yang digambarkan di atas (selepas transposisi yang sesuai), ia akan kelihatan seperti ini, C kini input, B ialah lapisan pertama dan A ialah lapisan kedua:
Juga, kecuali untuk warna fletching (biru di sebelah kiri, merah di sebelah kanan), isyarat visual kedua yang membezakan parameter kiri dan kanan ialah orientasinya: baris parameter di sebelah kiri adalah coplanar dengan baris keputusan - mereka bersama paksi yang sama (i) Bertindan. Contohnya (B @ C) di atas, kedua-dua pembayang boleh memberitahu kami bahawa B ialah parameter sebelah kiri.
3c Ungkapan binari
Untuk alat visualisasi, agar berguna, ia bukan sahaja mesti digunakan untuk contoh pengajaran yang mudah, tetapi juga mudah digunakan untuk ungkapan yang lebih kompleks. Dalam kes penggunaan dunia sebenar, komponen struktur utama ialah ungkapan binari - pendaraban matriks dengan subungkapan di sebelah kiri dan kanan. Ungkapan bentuk yang paling mudah (A @ B) @ (C @ D) divisualisasikan di sini:
3d Nota kecil: Pembahagian dan Keselarian
Penjelasan lengkap topik ini adalah di luar Ini ialah skop artikel ini, tetapi kita akan melihat utiliti praktikalnya kemudian dalam bahagian kepala perhatian. Tetapi untuk memanaskan badan, lihat dua contoh mudah untuk melihat bagaimana gaya visualisasi ini boleh membuat penaakulan tentang ungkapan kompaun selari sangat intuitif—hanya melalui pembahagian geometri yang ringkas. Contoh pertama ialah menggunakan pembahagian "data selari" tipikal pada contoh kesesakan berbilang lapisan gabungan kiri di atas. Kami membahagikan sepanjang i, membahagikan parameter kiri awal ("kelompok") dan semua hasil perantaraan ("pengaktifan"), tetapi bukan parameter berikutnya ("berat") - geometri ini menjadikan ungkapan Ia menjadi jelas yang pelakon dibahagikan dan kekal utuh:
Contoh kedua sukar difahami secara intuitif tanpa sokongan geometri yang jelas: ia menunjukkan cara untuk menyatakan subungkapan kiri dengan Parallelize ungkapan binari dengan membahagikan ungkapan, membahagikan anak sebelah kanan ungkapan di sepanjang paksi-i, dan membahagikan ungkapan induk di sepanjang paksi-k:

4 Melangkah jauh ke dalam kepala perhatian
🎜现在来看看 GPT-2 的注意力头 —— 具体来说是来自 NanoGPT 的 5 层第 4 头的 「gpt2」(small) 配置(层数 = 12,头数 = 12,嵌入数 = 768),通过 HuggingFace 使用了来自 OpenAI 的权重。输入激活取自在含 256 个 token 的 OpenWebText 训练样本上一次前向通过。
这个特定的头并无任何特殊之处,选择它主要是因为其计算的是一个非常常见的注意力模式,并且它位于模型中部,其中激活已经变得结构化并显示出一些有趣的纹理。

4a 结构
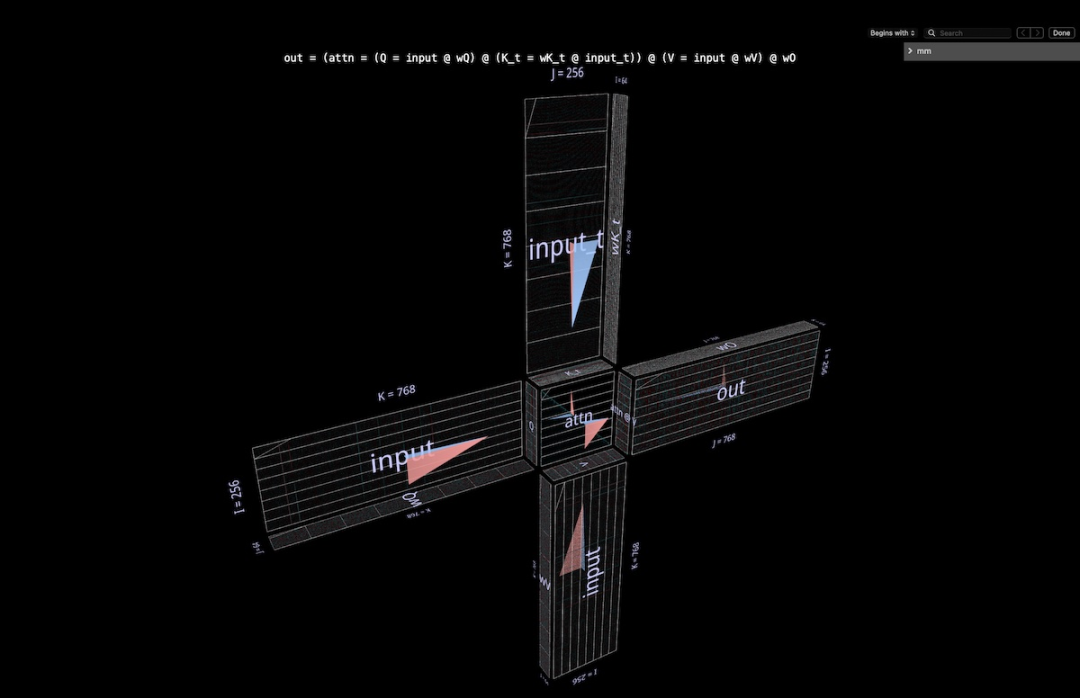
这个完整注意力头被可视化成了单个复合表达式,其始于输入,终于投影的输出。(注:为了保证自足性,这里按照 Megatron-LM 的描述对每个头执行输出投影。)
这一计算包含六次矩阵乘法:
Q = input @ wQ// 1K_t = wK_t @ input_t// 2V = input @ wV// 3attn = sdpa(Q @ K_t)// 4head_out = attn @ V // 5out = head_out @ wO // 6
简单描述一下这里在做什么:
风车的叶片为矩阵乘法 1、2、3 和 6:前一组是输入到 Q、K 和 V 的内投影;后者是从 attn @ V 回到嵌入维度的外投影。
中心有两个矩阵乘法;第一个计算的是注意力分数(后面的凸立方体),然后使用它们基于值向量得到输出 token(前面的凹立方体)。因果关系意味着注意力分数形成一个下三角形。
但读者最好能亲自详细探索这个工具,而不是只看截图或下面的视频,以便更详细地理解 —— 不管是其结构还是流过计算过程的实际值。
4b 计算和值
这里是注意力头的计算过程动画。具体来说,我们是看
sdpa (input @ wQ @ K_t) @ V @ wO
(即上面的矩阵乘法 1、4、5 和 6,其中 K_t 和 V 已经预先计算)是作为向量 - 矩阵积的融合链来计算:序列中的每一项都在一步之内从输入穿过注意力到输出。后面关于并行化的部分会提到更多有关这个动画的选择,但我们先看看计算的值能告诉我们什么。

我们可以看到很多有趣的东西:
在讨论注意力计算之前,可以看到低秩 Q 和 K_t 的形态是多么惊人。放大 Q @ K_t 向量 - 矩阵积动画,看起来会更加生动:Q 和 K 中大量通道(嵌入位置)在序列中看起来或多或少是恒定的,这意味着有用的注意力信号可能仅由一小部分嵌入驱动。理解和利用这种现象是 SysML ATOM transformer 效率项目的一部分。
也许人们最熟悉的是注意力矩阵中出现的强大但不完美的对角线。这是一种常见模式,出现在该模型(以及许多 Transformer)的许多注意力头中。它能产生局部注意力:紧邻输出 token 位置之前的小邻域中的值 token 很大程度上决定了输出 token 的内容模式。
然而,这个邻域的大小和其中各个 token 的影响变化很大 —— 这可以在注意力网格中的非对角 frost 中看到,也能在注意力矩阵沿序列下降时 attn [i] @ V 向量 - 矩阵积平面的波动模式中看到。
但请注意,局部邻域并不是唯一值得注意的东西:注意力网格的最左列(对应于序列的第一个 token )完全填充了非零(但波动)的值,这意味着每个输出 token 都会受到第一个值 token 一定程度的影响。
此外,当前 token 邻域和初始 token 之间的注意力分数主导性存在不精确但可辨别的振荡。该振荡的周期各有不同,但一般来说,一开始很短,然后沿序列向下移动而变长(类似地,在给定因果关系的情况下,与每一行的候选注意力 token 的数量相关)。
为了了解 (attn @ V) 的形成方式,不单独关注注意力是很重要的 ——V 也同等重要。每个输出项都是整个 V 向量的加权平均值:在注意力是完美对角线的极端情况下,attn @ V 只是 V 的精确副本。这里我们看到更有纹理的东西:可见的带状结构,其中特定 token 在注意力行的连续子序列上的得分很高,叠加在与 V 明显相似的矩阵上,但由于对角线较粗而有一些垂直遮挡。(旁注:根据 mm 参考指南,长按或按住 Control 键单击将显示可视化元素的实际数值。)
Perlu diingat bahawa memandangkan kita berada di lapisan tengah (lapisan 5), input kepada kepala perhatian ini ialah perwakilan perantaraan, bukan teks token asal. Oleh itu, corak yang dilihat dalam input adalah merangsang pemikiran mereka sendiri - khususnya, garis menegak yang kuat ialah kedudukan pembenaman khusus yang nilainya secara seragam mempunyai amplitud tinggi sepanjang jujukan yang panjang - kadang-kadang hampir penuh.
Tetapi apa yang menarik ialah vektor pertama dalam jujukan input adalah unik bukan sahaja memecahkan corak lajur amplitud tinggi ini, tetapi dalam hampir setiap kedudukan membawa nilai atipikal (nota sampingan: tidak digambarkan di sini, tetapi corak ini muncul berulang kali pada berbilang input sampel).
Nota: Berkenaan dua perkara terakhir, adalah wajar untuk mengulangi bahawa apa yang digambarkan di sini ialah pengiraan input sampel tunggal. Dalam amalan, didapati bahawa setiap kepala mempunyai corak ciri yang secara konsisten (walaupun tidak sama) dinyatakan merentasi set sampel yang agak besar, tetapi apabila melihat sebarang visualisasi yang mengandungi pengaktifan, seseorang perlu ingat bahawa pengedaran penuh input boleh menjejaskan secara halus idea dan gerak hati yang diilhamkan.
Akhir sekali, sekali lagi disyorkan untuk meneroka animasi secara langsung!
4c Terdapat banyak perbezaan menarik di kepala perhatian
Sebelum meneruskan, berikut adalah satu lagi demonstrasi yang menunjukkan cara mengkaji model untuk memahami Kegunaan kerja terperincinya.
Ini adalah satu lagi ketua perhatian GPT-2. Corak tingkah lakunya agak berbeza daripada Tahap 5 Head 4 - seperti yang dijangkakan kerana ia berada di bahagian model yang sangat berbeza. Pengepala ini terletak pada tahap pertama: Ketua 2 daripada tahap 0:

Mata yang patut diberi perhatian:
- #🎜🎜
- Taburan perhatian kepala ini sangat sekata. Ini mempunyai kesan menyampaikan purata tidak wajaran V (atau awalan sebab yang sesuai bagi V) kepada setiap baris attn@V seperti yang ditunjukkan dalam animasi: Semasa kita bergerak ke bawah segi tiga skor perhatian, attn[i] @ V vektor - Produk matriks mempunyai turun naik yang kecil, dan bukannya sekadar salinan V yang diperkecilkan dan diturunkan secara beransur-ansur.
- attn @ V mempunyai keseragaman menegak yang menakjubkan - corak nilai yang sama berterusan sepanjang jujukan dalam kawasan kolumnar besar yang tertanam. Seseorang boleh menganggap ini sebagai sifat yang dikongsi oleh setiap token.
- Nota sampingan: Di satu pihak, seseorang mungkin menjangkakan attn@V mempunyai sedikit konsistensi, memandangkan kesan pengagihan perhatian yang sangat sekata. Tetapi setiap baris terdiri daripada turutan sebab bagi V dan bukannya keseluruhan jujukan - mengapa ini tidak membawa kepada lebih banyak perubahan, seperti ubah bentuk progresif semasa anda bergerak ke bawah jujukan? Pemeriksaan visual menunjukkan bahawa V tidak seragam sepanjang panjangnya, jadi jawapannya mesti terletak pada beberapa sifat yang lebih halus bagi taburan nilainya.
- Akhir sekali, selepas unjuran luaran, output kepala ini harus lebih seragam dalam arah menegak.
- Kita boleh mendapat kesan yang kuat: kebanyakan maklumat yang disampaikan oleh ketua perhatian ini terdiri daripada atribut yang dikongsi oleh setiap token dalam urutan. Komposisi berat unjuran keluarannya boleh mengukuhkan gerak hati ini.
4d Kembali ke pengenalan: kebolehubah bebas
Mengimbas kembali, ia perlu diulangi: sebab mengapa kita boleh memberi tumpuan kepada bukan- remeh Apa yang menjadikan operasi komposit kelihatan dan mengekalkannya intuitif ialah sifat algebra yang penting (seperti cara bentuk parameter dikekang atau paksi selari yang bersilang dengan operasi mana) tidak memerlukan pemikiran tambahan: ia timbul secara langsung daripada sifat geometri objek yang divisualisasikan, dan Bukan peraturan tambahan untuk diingati. Sebagai contoh, dalam visualisasi kepala perhatian ini, dapat dilihat dengan jelas bahawa:- Q mempunyai panjang yang sama dengan attn @ V, K dan V mempunyai panjang yang sama, dan panjang pasangan ini bebas antara satu sama lain
- Q mempunyai lebar yang sama dengan K, dan V mempunyai lebar yang sama; as attn @ V. Pasangan ini Lebar semuanya bebas antara satu sama lain.
5 Parallelized Attention
Animasi kepala ke-4 daripada 5 lapisan visualisasi 4 di atas 6 pendaraban matriks dalam pengepala daya.
Ia divisualisasikan sebagai rantai gabungan produk-matriks vektor, mengesahkan gerak hati geometri: keseluruhan rantaian gabungan kiri dari input ke output berlapis di sepanjang paksi-i yang dikongsi dan boleh diselaraskan.
5a Contoh: Pembahagian sepanjang i
Untuk menyelaraskan pengiraan dalam amalan, kita boleh membahagikan input kepada ketulan di sepanjang paksi i. Kita boleh menggambarkan pembahagian ini dalam alat dengan menyatakan bahawa paksi yang diberikan dibahagikan kepada bilangan blok tertentu - 8 akan digunakan dalam contoh ini, tetapi tiada apa-apa yang istimewa tentang nombor itu.
Selain itu, visualisasi ini dengan jelas menunjukkan bahawa setiap pengiraan selari memerlukan wQ penuh (untuk unjuran dalam), K_t dan V (untuk perhatian) dan wO (untuk unjuran luar) kerana mereka Dimensi matriks yang tidak dipisahkan ini bersebelahan dengan partitioned. matriks:

5b Contoh: Dwi Pembahagian
Satu contoh pembahagian sepanjang berbilang paksi juga diberikan di sini. Untuk tujuan ini, di sini kami memilih untuk menggambarkan inovasi terkini dalam bidang ini, iaitu Block Parallel Transformer (BPT), yang berdasarkan beberapa hasil penyelidikan seperti Flash Attention Sila rujuk kertas: https://arxiv.org/. pdf/2305.19370.pdf
Pertama sekali, sekatan BPT di sepanjang i seperti yang diterangkan di atas - dan sebenarnya turut memanjangkan pembahagian jujukan mendatar ini hingga ke separuh lagi lapisan perhatian (FFN). (Penggambaran ini akan ditunjukkan kemudian.)
Untuk menangani sepenuhnya isu panjang konteks ini, tambahkan partition kedua pada MHA — partition pengiraan perhatian itu sendiri (iaitu partition sepanjang paksi-j Q @ K_t). Bersama-sama, kedua-dua partition ini membahagikan perhatian kepada grid blok:

Seperti yang jelas daripada visualisasi ini:
Pembahagian dwi ini dengan berkesan menyelesaikan masalah panjang konteks kerana kita kini boleh membahagikan panjang jujukan setiap kejadian secara visual dalam pengiraan perhatian.
"Julat" partition kedua: Jelas dari struktur geometri bahawa pengiraan unjuran dalaman K dan V boleh dipisahkan bersama dengan pendaraban matriks berganda teras.
Perhatikan perincian yang halus: pembayang visual di sini ialah kita juga boleh menyelarikan pendaraban matriks seterusnya attn @ V sepanjang k dan menjumlahkan hasil separa dalam gaya split-k, dengan itu menyelaraskan keseluruhan pendaraban matriks berganda. Tetapi softmax row-wise dalam sdpa() menambah keperluan: setiap baris perlu mempunyai semua penormalan segmennya sebelum mengira baris attn@V yang sepadan, yang menambah langkah baris demi baris Tambahan.
6 Saiz Lapisan Perhatian
Adalah diketahui bahawa separuh pertama lapisan perhatian (MHA) mempunyai keperluan pengiraan yang tinggi kerana kerumitan kuadratiknya, tetapi separuh kedua (FFN) juga mempunyai keperluannya sendiri, Ini disebabkan oleh lebar dimensi tersembunyinya, yang biasanya 4 kali lebar daripada dimensi terbenam model. Memvisualisasikan biojisim lapisan perhatian yang lengkap membantu membina pemahaman intuitif tentang bagaimana kedua-dua bahagian lapisan itu membandingkan antara satu sama lain.
6a Memvisualisasikan lapisan perhatian lengkap
Di bawah ialah lapisan perhatian lengkap, dengan separuh masa pertama (MHA) di belakang dan separuh kedua (FFN) di hadapan. Sekali lagi, anak panah menghala ke arah pengiraan.
Nota:
Penggambaran ini tidak menggambarkan satu kepala perhatian, tetapi menunjukkan pemberat dan unjuran Q/K/V yang tidak dihiris di sekitar pendaraban matriks berganda pusat. Sudah tentu ini tidak menggambarkan operasi MHA yang lengkap - tetapi matlamat di sini adalah untuk mendapatkan idea yang lebih jelas tentang saiz matriks relatif dalam dua bahagian lapisan, dan bukannya jumlah relatif pengiraan yang dilakukan oleh setiap separuh. (Selain itu, pemberat di sini menggunakan nilai rawak dan bukannya pemberat sebenar.)
Dimensi yang digunakan di sini dikecilkan untuk memastikan penyemak imbas boleh (secara relatif) membawanya, tetapi perkadarannya tetap sama (dari konfigurasi kecil NanoGPT ): Dimensi Benam Model = 192 (asal 768), dimensi benam FFN = 768 (asal 3072), panjang jujukan = 256 (asal 1024), walaupun panjang jujukan tidak mempunyai kesan asas pada model. (Secara visual, perubahan dalam panjang jujukan akan muncul sebagai perubahan dalam lebar bilah input, mengakibatkan perubahan dalam saiz pusat perhatian dan ketinggian satah menegak hiliran.)

6b Memvisualisasikan lapisan pembahagian BPT
Hanya Melihat ke belakang Blockwise Parallel Transformer, berikut ialah skema parallelization yang menggambarkan BPT dalam konteks keseluruhan lapisan perhatian (header diabaikan seperti di atas). Khususnya, perhatikan bagaimana pembahagian sepanjang i (blok jujukan) meluas melalui bahagian MHA dan FFN:

6c Pembahagian FFN
Kaedah visualisasi ini mencadangkan partition ortogonal tambahan kepada yang diterangkan di atas - pada separuh FFN lapisan perhatian, bahagikan pendaraban matriks berganda (attn_out @ FFN_1) @ FFN_2, pertama sepanjang j attn_out @ FFN_1 , dan kemudian lakukan pendaraban matriks berikutnya bersama k dengan FFN_2. Pembahagian ini memotong dua lapisan berat FFN untuk mengurangkan keperluan kapasiti bagi setiap komponen yang mengambil bahagian dalam pengiraan, dengan mengorbankan penjumlahan akhir keputusan separa.
Begini rupa kaedah pembahagian ini apabila digunakan pada lapisan perhatian yang tidak dibahagi:

Beginilah rupanya apabila digunakan pada lapisan yang dipartisi BPT:
penyahkodan pada masa visual satu token6
proses
Dalam proses penyahkodan satu-token-pada-satu masa autoregresif, vektor pertanyaan terdiri daripada satu token. Ia adalah pengajaran untuk membayangkan dalam fikiran anda bagaimana rupa lapisan perhatian dalam kes ini - satu baris pembenaman merentasi satah pemberat berjubin gergasi. Selain menekankan kebesaran pemberat berbanding pengaktifan, pandangan ini juga mengingatkan tanggapan bahawa K_t dan V berfungsi sama dengan lapisan yang dijana secara dinamik dalam MLP 6 lapisan, walaupun pengiraan mux/Demux boleh menjadikan surat-menyurat ini tidak tepat:
7 LoRA
Kertas kerja LoRA baru-baru ini "LoRA: Adaptasi Peringkat Rendah Model Bahasa Besar" menerangkan teknik penalaan halus yang cekap berdasarkan Idea: pemberat δ yang diperkenalkan semasa penalaan halus adalah peringkat rendah . Menurut kertas itu, ini "membolehkan kami secara tidak langsung melatih beberapa lapisan padat dalam rangkaian saraf dengan mengoptimumkan matriks penguraian peringkat perubahan lapisan padat semasa penyesuaian... sambil mengekalkan pemberat pra-latihan beku." IdeaRingkasnya, langkah utama ialah melatih faktor matriks berat dan bukannya matriks itu sendiri: gantikan tensor berat I x J dengan tensor I x K dan pendaraban matriks tensor K x J, di mana pastikan K adalah nilai yang kecil. Jika K cukup kecil, mungkin ada kemenangan besar dari segi saiz, tetapi ada pertukaran: mengurangkan K juga mengurangkan pangkat yang produk boleh nyatakan. Penjimatan saiz dan impak struktur pada keputusan digambarkan di sini dengan contoh, di sini pendaraban matriks rawak 128 x 4 parameter kiri dan 4 x 128 parameter kanan - iaitu, matriks 128 x 128 dengan pecahan peringkat 4 turun. Perhatikan corak menegak dan mendatar dalam L@R:
7b Sapukan LoRA pada kepala perhatian

Cara LoRA menggunakan kaedah penguraian ini untuk proses penalaan halus ialah:
untuk setiap beratmencipta penguraian peringkat rendah untuk diperhalusi dan melatih faktornya sambil mengekalkan pemberat asal
Selepas penalaan halus, darabkan setiap pasangan faktor peringkat rendah untuk mendapatkan matriks dalam bentuk berat asal; tensor, dan Tambah ini pada tensor berat pralatihan asal.
Penggambaran di bawah menunjukkan kepala perhatian dengan tensor beratnya wQ, wK_t, wV, wO digantikan dengan penguraian peringkat rendah wQ_A @ wQ_B dll. Secara visual, matriks faktor muncul sebagai pagar rendah di sepanjang tepi bilah kincir angin:
Atas ialah kandungan terperinci Cerapan tentang pendaraban matriks daripada perspektif 3D, beginilah rupa pemikiran AI. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!