 Peranti teknologi
Peranti teknologi AI
AI Pemikiran terbalik: Model bahasa penaakulan matematik baharu MetaMath melatih model besar
Pemikiran terbalik: Model bahasa penaakulan matematik baharu MetaMath melatih model besarPemikiran terbalik: Model bahasa penaakulan matematik baharu MetaMath melatih model besar
Penaakulan matematik yang kompleks ialah penunjuk penting untuk menilai keupayaan penaakulan model bahasa besar Pada masa ini, set data penaakulan matematik yang biasa digunakan mempunyai saiz sampel yang terhad dan kepelbagaian masalah yang tidak mencukupi, mengakibatkan fenomena "pembalikan laknat" secara besar-besaran. model bahasa, iaitu model yang dilatih mengenai "A Model bahasa "ialah B" tidak boleh digeneralisasikan kepada "B ialah A" [1]. Bentuk khusus fenomena ini dalam tugasan penaakulan matematik ialah: memandangkan masalah matematik, model bahasa pandai menggunakan penaakulan hadapan untuk menyelesaikan masalah tetapi tidak mempunyai keupayaan untuk menyelesaikan masalah dengan penaakulan songsang. Penaakulan songsang adalah sangat biasa dalam masalah matematik, seperti yang ditunjukkan dalam 2 contoh berikut.
1. Soalan klasik - Ayam dan arnab dalam sangkar yang sama
- Alasan ke hadapan: Terdapat 23 ekor ayam dan 12 ekor arnab di dalam sangkar itu? . Berapakah bilangan ayam dan arnab di dalam sangkar?
- 2. : James membeli x pek daging lembu sebanyak 4 paun Harga daging lembu ialah $5.50 sekilo
Untuk meningkatkan keupayaan penaakulan ke hadapan dan belakang model, penyelidik dari Cambridge, Universiti Sains dan Teknologi Hong Kong dan Huawei mencadangkan set data MetaMathQA berdasarkan dua set data matematik yang biasa digunakan (GSM8K dan MATH) : satu dengan liputan luas dan set data penaakulan matematik berkualiti tinggi. MetaMathQA terdiri daripada 395K pasangan soalan matematik songsang hadapan yang dijana oleh model bahasa yang besar. Mereka memperhalusi LLaMA-2 pada set data MetaMathQA untuk mendapatkan MetaMath, model bahasa besar yang memfokuskan pada penaakulan matematik (ke hadapan dan songsang), yang mencapai SOTA pada set data penaakulan matematik. Dataset MetaMathQA dan model MetaMath pada skala yang berbeza telah dibuka sumbernya untuk digunakan oleh penyelidik.
- Alamat projek: https://meta-math.github.io/
: https
: alamat //huggingface.co/datasets/meta-math/MetaMathQA
- Alamat model: https://huggingface.co/meta-math
- Alamat kod: https://github.com/meta-math/ MetaMath
- Dalam set data GSM8K-Backward, kami membina percubaan inferens songsang. Keputusan eksperimen menunjukkan bahawa berbanding dengan kaedah seperti SFT, RFT dan WizardMath, kaedah semasa berprestasi buruk pada masalah inferens songsang. Sebaliknya, model MetaMath mencapai prestasi cemerlang dalam kedua-dua inferens ke hadapan dan songsang
- Kaedah

 Kaedah
Kaedah
MetaMathQGA mengandungi empat kaedah pengukuhan 1. Pembesaran Jawapan:
- Diberikan soalan, rantaian pemikiran yang boleh mendapatkan hasil yang betul dijana melalui model bahasa yang besar sebagai penambahan data.
- Soalan: James membeli 5 bungkus daging lembu sebanyak 4 paun setiap satu Harga daging lembu ialah $5.50 sekilo? setiap satu, jadi dia membeli sejumlah 5 * 4 = 20 paun daging lembu adalah $5.50 setiap paun, jadi dia membayar 20 * $5.50 = $110.
2 Soalan (peningkatan penulisan semula soalan): Diberi meta-soalan, tulis semula soalan melalui model bahasa yang besar dan jana rantai pemikiran yang mendapat hasil yang betul sebagai penambahan data.
- Soalan: Berapakah jumlah yang James bayar apabila dia membeli 5 pek daging lembu, setiap satu seberat 4 paun, pada harga $5.50 setiap paun?
- Jawapan: Setiap pek daging lembu seberat 4 paun, jadi 5 pek berat 4 * 5 = 20 paun jumlah harga setiap paun daging lembu ialah $5.50, jadi jumlah kos untuk 20 paun ialah 20 * $5.50 = $110. Oleh itu, James membayar sejumlah $110.
3. Soalan FOBAR (Peningkatan Soalan Songsang FOBAR): Diberi meta-soalan, nombor dalam keadaan topeng ialah x, diberi jawapan asal dan songsang x untuk menghasilkan soalan songsang, dan berdasarkan kepada Masalah songsang ini menjana rantaian pemikiran yang betul untuk melakukan penambahan data (contoh penyongsangan: "Jika kita tahu jawapan kepada soalan di atas ialah 110, apakah nilai pembolehubah x yang tidak diketahui?").
- question: James membeli x pek daging lembu yang masing -masing 4 paun. pembolehubah yang tidak diketahui x?
- Jawapan: James membeli x pek daging lembu yang 4 paun setiap satu, jadi dia membeli sejumlah 4x paun daging lembu Harga daging lembu ialah $5.50 setiap paun, jadi jumlah kos daging lembu itu ialah 5.50 * 4x = 22x Kami diberi bahawa jumlah kos ialah $110, jadi kita boleh menulis: 22x = 110. Membahagikan kedua-dua belah dengan 22, kita dapat: x = 5. Nilai x ialah 5.
4. Soalan Pengesahan Kendiri (Peningkatan soalan songsang Pengesahan Kendiri): Berdasarkan FOBAR, bahagian soalan songsang ditulis semula sebagai pernyataan yang dinyatakan melalui model bahasa yang besar untuk melakukan penambahan data (contoh yang ditulis semula: "Berapa banyak adakah dia membayar?” (dengan jawapan 110) ditulis semula sebagai “Dia membayar 110”). . masalah, kita perlu menentukan nilai x, yang mewakili bilangan pek daging lembu yang dibeli oleh James Setiap pek daging lembu seberat 4 paun dan berharga $5.50 setiap paun Jumlah yang dibayar oleh James ialah $110 seperti berikut: Bilangan pek daging lembu * Berat setiap pek * Harga setiap paun = Jumlah amaun yang dibayar; kita bahagikan kedua-dua belah persamaan dengan 22: 22x / 22 = $110 / 22 Nilai x ialah 5. Keputusan eksperimen pada set data penaakulan matematik (GSM8K dan MATH) menunjukkan bahawa MetaMath jauh lebih baik daripada yang sedia ada; model LLM sumber terbuka dalam prestasi, dan tidak memerlukan penggunaan alat luaran (seperti jurubahasa kod). Antaranya, model MetaMath-7B kami mencapai ketepatan 66.5% pada GSM8K dan 19.8% pada MATH, iaitu 11.6% dan 9.1% lebih tinggi daripada model terkini skala yang sama. Perlu dinyatakan secara khusus bahawa MetaMath-70B mencapai ketepatan 82.3% pada GSM8K, melebihi GPT-3.5-Turbo
- Menurut "Hipotesis Penjajaran Permukaan" [2], keupayaan model bahasa besar datang dari pra- latihan, manakala data daripada tugasan hiliran mengaktifkan keupayaan sedia ada model bahasa yang dipelajari semasa pra-latihan. Oleh itu, ini menimbulkan dua persoalan penting: (i) jenis data yang manakah mengaktifkan pengetahuan terpendam dengan paling berkesan, dan (ii) mengapa satu set data lebih baik pada pengaktifan sedemikian daripada yang lain?
- Mengapa MetaMathQA berguna? Meningkatkan kualiti (Perplexity) data rantai pemikiran


Mengapa MetaMathQA berguna? Meningkatkan kepelbagaian data rantaian pemikiran

Dengan membandingkan keuntungan kepelbagaian data dan keuntungan ketepatan model, penyelidik mendapati bahawa pengenalan perumusan semula, FOBAR dan SV meningkat sebanyak jumlah yang sama Pelbagai data telah membawa keuntungan kepelbagaian yang ketara dan meningkatkan ketepatan model dengan ketara. Sebaliknya, menggunakan penambahan jawapan sahaja menghasilkan ketepuan ketepatan yang ketara. Selepas ketepatan mencapai ketepuan, menambah data AnsAug hanya akan membawa peningkatan prestasi terhad
Atas ialah kandungan terperinci Pemikiran terbalik: Model bahasa penaakulan matematik baharu MetaMath melatih model besar. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Alat panggilan di LLMSApr 14, 2025 am 11:28 AM
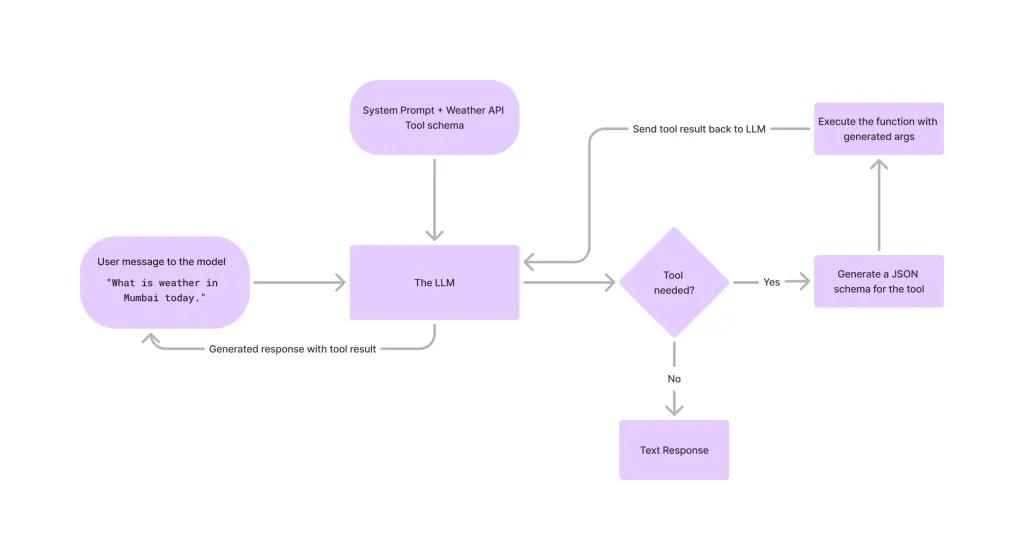
Alat panggilan di LLMSApr 14, 2025 am 11:28 AMModel bahasa yang besar (LLMS) telah melonjak populariti, dengan ciri-ciri alat yang secara dramatik memperluaskan keupayaan mereka di luar penjanaan teks mudah. Sekarang, LLMS dapat mengendalikan tugas automasi yang kompleks seperti penciptaan UI dinamik dan autonomi a
 Bagaimana permainan ADHD, alat kesihatan & chatbots AI mengubah kesihatan globalApr 14, 2025 am 11:27 AM
Bagaimana permainan ADHD, alat kesihatan & chatbots AI mengubah kesihatan globalApr 14, 2025 am 11:27 AMBolehkah permainan video meringankan kebimbangan, membina fokus, atau menyokong kanak -kanak dengan ADHD? Memandangkan cabaran penjagaan kesihatan melonjak di seluruh dunia - terutamanya di kalangan belia - inovator beralih kepada alat yang tidak mungkin: permainan video. Sekarang salah satu hiburan terbesar di dunia Indus
 Input PBB pada AI: Pemenang, Losers, dan PeluangApr 14, 2025 am 11:25 AM
Input PBB pada AI: Pemenang, Losers, dan PeluangApr 14, 2025 am 11:25 AM"Sejarah telah menunjukkan bahawa walaupun kemajuan teknologi memacu pertumbuhan ekonomi, ia tidak sendiri memastikan pengagihan pendapatan yang saksama atau menggalakkan pembangunan manusia yang inklusif," tulis Rebeca Grynspan, Setiausaha Agung Unctad, dalam Mukadimah.
 Kemahiran rundingan pembelajaran melalui AI generatifApr 14, 2025 am 11:23 AM
Kemahiran rundingan pembelajaran melalui AI generatifApr 14, 2025 am 11:23 AMEasy-peasy, gunakan AI Generatif sebagai tutor rundingan dan rakan kongsi sparring anda. Mari kita bercakap mengenainya. Analisis terobosan AI yang inovatif ini adalah sebahagian daripada liputan lajur Forbes yang berterusan pada AI terkini, termasuk mengenal pasti dan menjelaskan
 Ted mendedahkan dari Openai, Google, Meta Heads to Court, selfie dengan diri sayaApr 14, 2025 am 11:22 AM
Ted mendedahkan dari Openai, Google, Meta Heads to Court, selfie dengan diri sayaApr 14, 2025 am 11:22 AMPersidangan TED2025, yang diadakan di Vancouver, membungkus edisi ke -36 semalam, 11 April. Ia menampilkan 80 penceramah dari lebih daripada 60 negara, termasuk Sam Altman, Eric Schmidt, dan Palmer Luckey. Tema Ted, "Kemanusiaan Reimagined," telah disesuaikan dibuat
 Joseph Stiglitz memberi amaran tentang ketidaksamaan yang menjulang di tengah -tengah kuasa monopoli AIApr 14, 2025 am 11:21 AM
Joseph Stiglitz memberi amaran tentang ketidaksamaan yang menjulang di tengah -tengah kuasa monopoli AIApr 14, 2025 am 11:21 AMJoseph Stiglitz adalah ahli ekonomi yang terkenal dan penerima Hadiah Nobel dalam Ekonomi pada tahun 2001. Stiglitz berpendapat bahawa AI dapat memburukkan lagi ketidaksamaan dan kuasa yang disatukan di tangan beberapa syarikat dominan, akhirnya menjejaskan ekonomi
 Apakah pangkalan data graf?Apr 14, 2025 am 11:19 AM
Apakah pangkalan data graf?Apr 14, 2025 am 11:19 AMPangkalan Data Graf: Merevolusi Pengurusan Data Melalui Hubungan Apabila data berkembang dan ciri -cirinya berkembang di pelbagai bidang, pangkalan data grafik muncul sebagai penyelesaian transformatif untuk menguruskan data yang saling berkaitan. Tidak seperti tradisional
 LLM Routing: Strategi, Teknik, dan Pelaksanaan PythonApr 14, 2025 am 11:14 AM
LLM Routing: Strategi, Teknik, dan Pelaksanaan PythonApr 14, 2025 am 11:14 AMRouting Model Besar (LLM): Mengoptimumkan Prestasi melalui Pengedaran Tugas Pintar Landskap LLM yang pesat berkembang membentangkan pelbagai model, masing -masing dengan kekuatan dan kelemahan yang unik. Beberapa cemerlang di Gen Kandungan Kreatif


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

SublimeText3 Linux versi baharu
SublimeText3 Linux versi terkini

Penyesuai Pelayan SAP NetWeaver untuk Eclipse
Integrasikan Eclipse dengan pelayan aplikasi SAP NetWeaver.

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Dreamweaver Mac版
Alat pembangunan web visual

DVWA
Damn Vulnerable Web App (DVWA) ialah aplikasi web PHP/MySQL yang sangat terdedah. Matlamat utamanya adalah untuk menjadi bantuan bagi profesional keselamatan untuk menguji kemahiran dan alatan mereka dalam persekitaran undang-undang, untuk membantu pembangun web lebih memahami proses mengamankan aplikasi web, dan untuk membantu guru/pelajar mengajar/belajar dalam persekitaran bilik darjah Aplikasi web keselamatan. Matlamat DVWA adalah untuk mempraktikkan beberapa kelemahan web yang paling biasa melalui antara muka yang mudah dan mudah, dengan pelbagai tahap kesukaran. Sila ambil perhatian bahawa perisian ini





