Buktikan bahawa set dominan graf ialah NP-lengkap

Set dominan graf ialah masalah lengkap NP, iaitu subset bucu supaya setiap bucu atau bucu bersebelahan dalam subset berada dalam subset. Bentuk penuh NP ialah "polinomial bukan deterministik" yang akan menyemak masalah dalam masa polinomial, bermakna kita boleh menyemak dalam masa polinomial sama ada penyelesaiannya betul. Masa polinomial mempunyai kerumitan terbaik untuk kod seperti kerumitan masa carian linear – n, carian binari – logn, isihan gabungan - n(log)n dsb. Graf NP-lengkap menyediakan penyelesaian yang baik dalam masa yang munasabah. Aplikasi ini digunakan dalam bidang seperti kawalan rangkaian, penciptaan topologi di makmal komputer, rangkaian sosial, dan pengkomputeran teragih.

Mari kita memahami dan menyemak sama ada nod mempunyai set dominan bagi graf lengkap NP.

Puncak dikatakan menguasai dirinya dan setiap jirannya.

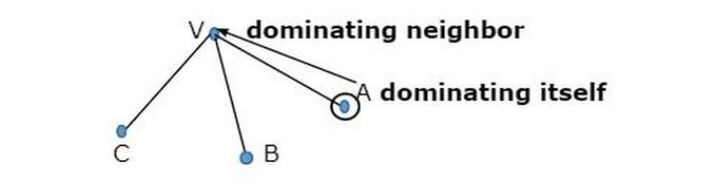
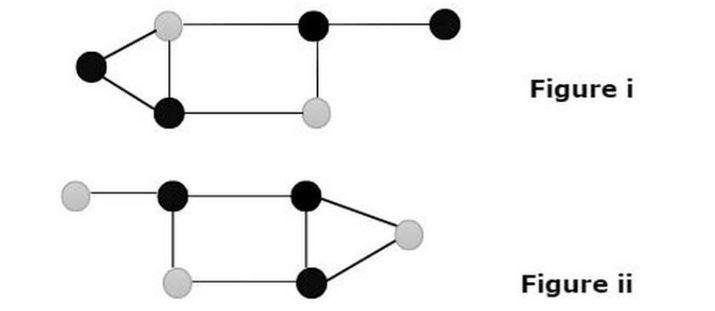
Kami melihat dua graf yang menunjukkan nod dalam graf di mana warna kelabu mendominasi alam semula jadi.

G = V, E

Parameter

G dianggap sebagai graf, V dianggap sebagai bucu, dan E dianggap sebagai tepi.

Diberi graf G(V, E) dan integer k, tentukan sama ada graf itu mempunyai set mendominasi saiz k. Input yang dinyatakan sebagai masalah dianggap sebagai contoh masalah. Graf G(V, E) dan integer k berfungsi sebagai contoh masalah set mendominasi, yang menanyakan sama ada graf G boleh mempunyai set mendominasi dalam G. Memandangkan takrifan masalah NP-lengkap ialah masalah yang NP dan NP-keras, membuktikan bahawa masalah adalah NP-lengkap mempunyai dua komponen −

Dominator set dalam masalah NP-lengkap

Jika terdapat masalah NP Y yang berkurangan kepada X dalam masa polinomial, maka X ialah masalah NP-lengkap. Masalah NP-lengkap sama sukarnya dengan masalah NP. Masalah ialah NP-Complete jika ia merupakan sebahagian daripada masalah NP dan masalah NP-Hard. Mesin Turing tidak tentu boleh menyelesaikan masalah lengkap NP dalam masa polinomial. Apabila masalah adalah np-lengkap, ia mempunyai kombinasi np dan np-hard.

Ini bermakna masalah dengan penyelesaian np boleh disahkan dalam masa polinomial.

Contoh sebenar NP complete mempunyai set yang mendominasi seperti -

• Masalah membuat keputusan.

• Grafik adalah konsisten.

Algoritma carian bukan deterministik

NP_search( key ) {
   arraylist[100];
   i = array_check(key);
   if(list[i]==key) {
      searching found at index i.
   } else {
      searching found at index i.
   }
}

Jadi, jumlah kerumitan masa algoritma ini ialah O(1), tetapi kami tidak tahu teknik carian mana yang lebih berguna untuk menyelesaikan masalah ini, ini dipanggil algoritma bukan deterministik.

Dominator ditetapkan dalam masalah NP-keras

Masalah X adalah sukar NP jika wujud masalah Y lengkap NP yang berkurangan kepada masalah X dalam masa polinomial. Masalah NP-keras adalah sekeras masalah NP-lengkap. Masalah NP-hard tidak semestinya tergolong dalam kategori NP.

Jika setiap masalah NP boleh diselesaikan dalam masa polinomial, ia dipanggil NP-Hard. Banyak kali, masalah khusus digunakan untuk menyelesaikan dan mengurangkan masalah lain.

Contoh sebenar

NP-hard mempunyai set yang mendominasi seperti -

• Kitaran Hamiltonian

• Isu pengoptimuman

• Laluan terpendek

Kesimpulan

Kami mempelajari konsep bahawa set dominan graf ialah NP-lengkap. Kami melihat bagaimana matematik diskret merupakan aspek penting yang menghubungkan masalah ini, seperti kitaran Hamilton, laluan terpendek, dsb. Dalam istilah pengaturcaraan, masalah NP-lengkap ialah kelas masalah yang sukar dicari tetapi penyelesaiannya boleh disahkan secara langsung dalam masa polinomial.

Atas ialah kandungan terperinci Buktikan bahawa set dominan graf ialah NP-lengkap. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!