Rumah >pembangunan bahagian belakang >C++ >Gunakan penambahan atau penolakan untuk mendapatkan bilangan langkah minimum untuk N pada setiap langkah
Gunakan penambahan atau penolakan untuk mendapatkan bilangan langkah minimum untuk N pada setiap langkah
- WBOYke hadapan
- 2023-09-16 13:13:22734semak imbas
Daripada penyataan masalah di atas, tugas kita adalah untuk mendapatkan bilangan langkah minimum yang mana nombor N yang diberikan boleh diperoleh menggunakan penambahan atau penolakan dalam setiap langkah. Kita boleh memahami bahawa kita perlu mencetak bilangan langkah minimum yang boleh dilakukan dan susunan langkah untuk mana-mana integer N tertentu, dengan menambah dan menolak nombor langkah untuk tiba pada nombor bermula dari 0.
Dalam set masalah ini, kita boleh menambah atau menolak nombor yang sama dengan bilangan langkah ke kedudukan semasa pada setiap langkah. Sebagai contoh, kita boleh menambah 1 atau -1 dalam langkah 1. Selanjutnya kita boleh menambah 2 atau -2 dalam langkah 2 dan seterusnya. Kita boleh menambah atau menolak nombor pada setiap langkah bergantung pada keadaan.
Cabaran utama masalah ini ialah kita perlu melakukan bilangan langkah minimum bermula dari 0 untuk mencapai N. Marilah kita memahami isu ini dengan lebih baik dengan contoh.
Contoh yang diberikan di bawah akan menunjukkan kepada anda setiap nombor yang kami dapat dalam 2 langkah bermula dari 0 dengan melakukan operasi di atas.
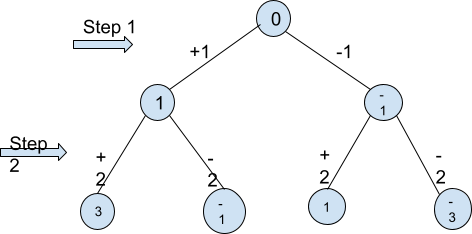
Sebagai contoh, andaikan kita mempunyai N=1.
Output
Minimum no of steps: 1 Sequence of steps: 1
Penerangan
Kita boleh mencapai 1 dalam dua cara -
Hanya tambahkan 1 kepada langkah 1 untuk beralih dari 0 kepada 1, yang mengambil 1 langkah.
Tolak 1 dalam langkah 1 untuk bergerak dari 0 kepada -1, kemudian tambah 2 dalam langkah 2 untuk beralih dari -1 kepada 1, yang mengambil 2 langkah.
Oleh kerana masalah menyatakan bahawa kita memerlukan bilangan langkah minimum untuk mencapai sebarang nombor N, output yang dikehendaki untuk input ini ialah 1.
Untuk, N=3
Output
Minimum no of steps: 2 Sequence of steps: 1 2
Penerangan
Kami menambah 1 dalam langkah 1 untuk beralih dari 0 kepada 1, kemudian menambah 2 dalam langkah 2 untuk beralih dari 1 kepada 3.
kaedah
Cara terbaik untuk menyelesaikan masalah adalah dengan terlebih dahulu mengetahui sama ada N ialah nombor positif atau negatif. Kita mesti menambah atau menolak bilangan langkah yang sesuai masing-masing untuk menyelesaikan masalah.
Jika N ialah nombor positif, teruskan menambah langkah sehingga jumlahnya lebih besar daripada atau sama dengan N.
Begitu juga, jika N ialah nombor negatif, teruskan menolak bilangan langkah sehingga jumlahnya lebih besar daripada atau sama dengan N.
Jika jumlahnya sama dengan N dalam kes di atas, kembalikan bilangan langkah dan susunan langkah. Masalah utama ialah mengendalikan situasi apabila N melebihi.
Setelah jumlah melebihi N, semak sama ada (jumlah-N) genap atau ganjil.
-
Jika (jumlah-N) genap, maka kita perlu melakukan penolakan dalam langkah (jumlah-N)/2 untuk mencapai N.
Marilah kita memahami kes ini dengan lebih baik melalui contoh yang sesuai.
Untuk, N=8
1+2+3+4=10, iaitu lebih daripada 8.
Kerana 10-8=2 ialah nombor genap. Jadi kita akan tolak dalam langkah 2/2, iaitu
Langkah 1. Oleh itu, susunan langkahnya ialah -1 2 3 4 dan minimum
Bilangan langkah untuk mencapai N ialah 4.
-
Jika (jumlah-N) ialah nombor ganjil, mula-mula tentukan sama ada nombor yang jumlahnya melebihi N dalam langkah sebelumnya adalah genap atau ganjil.
Jika langkah sebelumnya adalah ganjil, maka lakukan langkah dengan menambah nombor langkah seterusnya yang akan menjadikan (jumlah-N) kita genap dan kemudian lakukan langkah di atas untuk mendapatkan hasil yang diinginkan.
Sebagai contoh, N=9
1+2+3+4=10, iaitu lebih daripada 9.
Oleh kerana 10-9=1, ini adalah nombor ganjil. Langkah seterusnya ialah 5, iaitu nombor ganjil, jadi kita hanya melakukan satu langkah dan menambah 5 kepada jumlah untuk mendapatkan 15, menjadikan (jumlah-N)=6. Melakukan penolakan dalam langkah 3 akan memberikan anda urutan 1 2 -3 4 5, iaitu output yang diingini.
Andaikan langkah sebelumnya ialah nombor genap Dalam kes ini, kita perlu melakukan dua langkah, tambah langkah ke-i dan tolak langkah (i+1) untuk mendapatkan. (jumlah - N) sebagai nombor genap untuk mendapatkan urutan langkah yang dikehendaki.
untuk N=5
1+2+3=6, lebih daripada 5.
Oleh kerana (jumlah-N) =1, kami akan mempertimbangkan langkah terakhir apabila su melebihi nombor N. Oleh kerana ia adalah nombor genap, kami akan melakukan dua langkah, langkah 4 dan langkah 5. Tugas kita adalah untuk membuat (jumlah-N) walaupun begitu, dengan menambah dalam langkah 4 dan menolak dalam langkah 5 kita boleh membuat (jumlah-N) walaupun 1 ditolak daripada jumlah. Oleh kerana (jumlah-N) sama dengan 0, kita mendapat N. Oleh itu, urutannya ialah 1 2 3 4 -5.
Contoh
Berikut ialah kod C++ kaedah ini -
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
vector <int> steps; // for storing the sequence
int totalSum=0;
int temp=0;
if(n>=0){ // if n is positive then temp will store positive
temp=1;
} else {
temp=-1; // n is negative then temp will store negative
}
n=abs(n);
int step=0;
for(step=1;totalSum<n;step++){ // for storing the steps till sum is not greater than n
steps.push_back(temp*step);
totalSum=totalSum+step;
}
if(totalSum>temp*n) { //when sum greater than n
if(step%2==0) { //when step is even
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the addition of next step
steps.push_back((temp*-1)*(step+1)); // store the subtraction of next step
totalSum--; //make totalSum even
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
} else { //when step is odd
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the next addition value
totalSum+=step;
step++;
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
}
}
//print the minimum number of steps taken
cout<<"The minimum number of steps : "<<steps.size()<<endl;
//print the steps is stored in vector
cout<<"Sequence of steps : ";
for(int i=0;i<steps.size();i++){
cout<<steps[i]<<" ";
}
}
int main(){
int m=17;
minimumStep(m);
return 0;
}
Output
The minimum number of steps : 6 Sequence of steps : 1 -2 3 4 5 6
Kerumitan masa: O(sqrt(N))
Kerumitan ruang: O(sqrt(N))
KESIMPULAN
Dalam artikel ini, kami cuba menerangkan kaedah untuk mencari bilangan langkah minimum untuk mencapai N dengan menambah atau menolak pada setiap langkah dan mencetak jujukan. Saya harap artikel ini membantu anda mempelajari konsep ini dengan lebih baik.
Atas ialah kandungan terperinci Gunakan penambahan atau penolakan untuk mendapatkan bilangan langkah minimum untuk N pada setiap langkah. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Ralat kompilasi C++: Fail pengepala dirujuk beberapa kali, bagaimana untuk menyelesaikannya?
- Ralat kompilasi C++: parameter fungsi yang salah, bagaimana untuk memperbaikinya?
- Ralat C++: Pembina mesti diisytiharkan di kawasan awam, bagaimana untuk menanganinya?
- Pengurusan proses dan penyegerakan benang dalam C++
- Bagaimana untuk menangani masalah pemisahan data dalam pembangunan C++

