Permainan padanan nombor?

Number Connect ialah teka-teki logik yang melibatkan mencari laluan yang menghubungkan nombor dalam grid.

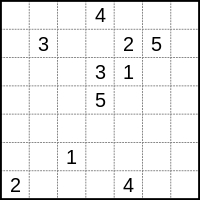
Contoh mudah penyelesaian teka-teki Numberlink Numberlink puzzle

#🎜 🎜🎜#RULE

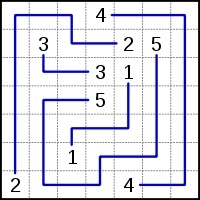
- Pemain mesti memadankan semua nombor padanan pada grid dengan satu garisan berterusan (atau laluan). Garis tidak boleh mencapah atau bersilang, dan nombor mestilah di hujung setiap baris (iaitu bukan di tengah). Masalah dianggap direka dengan baik hanya jika ia mempunyai penyelesaian yang unik dan semua sel dalam grid diisi, walaupun sesetengah pereka Numberlink tidak menyatakan perkara ini.

游戏

- Pertimbangkan susunan n×n segi empat sama. Beberapa petak kosong, ada yang pepejal, dan beberapa petak tidak pepejal ditandakan dengan integer 1, 2, 3,... Setiap integer menduduki dua petak berbeza di papan. Tugas pemain adalah untuk menyambungkan dua kejadian setiap integer di papan melalui laluan mudah menggunakan hanya pergerakan mendatar dan menegak. Dua laluan berbeza tidak dibenarkan bersilang. Tiada laluan boleh mengandungi sebarang blok pepejal (tiada blok pepejal dibenarkan pada mana-mana laluan). Akhir sekali, semua petak bukan pepejal mesti diisi dengan laluan.

Algoritma

- Untuk menyediakan teka-teki rawak yang cekap diberikan saiz papan n×n, kami mula-mula menjana laluan terputus mudah rawak pada papan. Jika terdapat beberapa blok terpencil yang kekal di luar semua laluan yang dijana, tandakan blok terpencil ini sebagai pepejal (dilarang). Kami kemudian menggunakan titik akhir laluan dan senarai petak pepejal sebagai teka-teki. Jadi, kami mula-mula menjana penyelesaian dan kemudian menyelesaikan teka-teki daripada penyelesaian. Laluan dan petak pepejal membahagikan papan catur n×n kepada bahagian-bahagian. Kami menggunakan struktur data carian kesatuan untuk menjana pemisahan ini. Struktur data mengendalikan subset n^2 petak pada papan.

Penjelasan

Cari petak (i, j) dan (k, l) secara rawak pada papan catur supaya: (a) (i , j) dan (k, l) adalah berjiran antara satu sama lain, dan (b) (i, j) mahupun (k, l) tidak tergolong dalam mana-mana laluan yang dihasilkan setakat ini. Jika tiada sepasang segi empat sama ditemui pada keseluruhan papan, kegagalan dikembalikan /* Di sini, (i, j) dan (k, l) ialah dua petak pertama laluan baharu yang akan dibina. *
Gabungkan dua pokok cari kesatuan yang mengandungi (i, j) dan (k, l).
Ulangi langkah berikut sehingga laluan semasa tidak dapat dilanjutkan: Namakan semula (i, j) kepada (k, l). Cari secara rawak petak jiran (k, l) bagi (i, j) supaya: (a) (k, l) tidak tergolong dalam mana-mana laluan yang dijana setakat ini (termasuk laluan semasa) (b) Pada laluan semasa yang dibina sebahagiannya ( Satu-satunya jiran i, j) ialah (k, l).
Jika tiada blok jiran (k, l) seperti itu ditemui, laluan tidak boleh dilanjutkan lagi, jadi gelung terputus

• #🎜🎜 #

  Jika tidak, cantumkan dua pokok pencarian kesatuan yang mengandungi (i, j) dan (k, l).

• Tetapkan bendera blok permulaan dan blok penamat laluan baharu.

• Kembali dengan jayanya
Enter ##🎜🎜🎜🎜🎜 🎜#

Output

Penyelesaian kepada jadual di atas

| || || || || || || 4 |
| || || || || || 3 || |
| || || 2 || 2 || || || 3 |
| || || || || X || || 1 |
| || || 6 || || || 7 || 7 |
| 5 || 4 || || X || || X || 1 |
| || 5 || || 6 || || || |

Contoh

| 4 || 4 || 4 || 4 || 4 || 4 || 4 |
| 4 || 1 || 1 || 1 || 1 || 3 || 3 |
| 4 || 1 || 2 || 2 || 1 || 1 || 3 |
| 4 || 1 || 1 || 1 || X || 1 || 1 |
| 4 || 4 || 6 || 1 || 1 || 7 || 7 |
| 5 || 4 || 6 || X || 1 || X || 1 |
| 5 || 5 || 6 || 6 || 1 || 1 || 1 |

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
   struct _node *parent;
   int rank;
   int path_number;
   int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
   int i, j;
   for (i=0;i<n;i++){
      for (j=0;j<n;j++){
         node *np;
         np = (node *)malloc(sizeof(node));
         np->rank = 0;
         np->parent = NULL;
         np->path_number = 0;
         np->endpoint = 0;
         arr[i][j] = np;
      }
   }
}
/*

#🎜🎜🎜 #

Input:a node
Output:the set pointer of the set the node belongs to

Penerangan

- Mendapat nod dan mengembalikan penunjuk yang ditetapkan. */

node *findset(node *n) {
   if (n->parent != NULL)
      n = n->parent;
   return n;
}
void setunion(node *x, node *y) {
   x = findset(x);
   y = findset(y);
   if (x->rank > y->rank)
      y->parent = x;
   else {
      x->parent = y;
      if(x->rank == y->rank)
         y->rank++;
   }
}
int neighbour(int n, node ***arr) {
   int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
   int k = rand()%(n*n);
   while (ct < (n*n)) {
      k %= (n*n);
      i1 = k/n;
      j1 = k%n;
      if (arr[i1][j1]->path_number==0) {
         int kk = rand()%4;
         int cc = 0;
         switch (kk) {
            case 0: i2= i1-1;
               j2= j1-0;
            if(i2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 1: i2= i1-0;
               j2= j1-1;
            if(j2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 2: i2= i1+1;
            j2= j1-0;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 3: i2= i1-0;
            j2= j1+1;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 4: if(cc==4)
               break;
            i2= i1-1;
            j2= j1-0;
            if(i2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 5: if(cc==4)
               break;
            i2= i1-0;
            j2= j1-1;
            if(j2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 6: if(cc==4)
               break;
            i2= i1+1;
            j2= j1-0;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 7: if(cc==4)
               break;
            i2= i1-0;
            j2= j1+1;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
         }
      }
      if(flag==1)
         break;
         ct++;
         k++;
   }
   if(ct<n*n) {
      k2= (i2*n)+j2;
      return k*(n*n)+k2;
   } else {
      return -1;
   }
}
int checkneigh(int k1, int k2, int n, node ***arr) {
   int i= k2/n;
   int j= k2%n;
   int ii= k1/n;
   int jj= k1%n;
   int ct=0;
   if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
      ct++;
   if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
      ct++;
   if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
      ct++;
   if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
      ct++;
   if(ct>1)
      return 0;
   else
      return 1;
}
int valid_next(int k, int n, node ***arr) {
   int i1, i2, j1, j2, a, b, kk, stat,ct=0;
   int flag=0;
   i1= k/n;
   j1= k%n;
   kk= rand()%4;
   switch(kk) {
      case 0: i2= i1-1;
         j2= j1-0;
      if(i2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 1: i2= i1-0;
         j2= j1-1;
      if(j2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 2: i2= i1+1;
         j2= j1-0;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 3: i2= i1-0;
         j2= j1+1;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 4: if(ct==4)
         break;
      i2= i1-1;
      j2= j1-0;
      if(i2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 5: if(ct==4)
         break;
      i2= i1-0;
      j2= j1-1;
      if(j2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 6: if(ct==4)
         break;
      i2= i1+1;
      j2= j1-0;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 7: if(ct==4)
         break;
      i2= i1-0;
      j2= j1+1;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
   }
   //printf("flag- %d</p><p>",flag);
   if(flag==0)
      return -1;
   if(flag) {
      //printf("value sent- %d</p><p>", i2*n + j2);
      return (i2*n)+j2;
   }
}
int addpath(node ***arr, int n, int ptno) {
   int a,b,k1,k2;
   int i1,j1,i2,j2;
   k2= neighbour( n, arr);
   if(k2==-1) //no valid pair found to start with
      return 0;
   k1= k2/(n*n);
   k2= k2%(n*n);
   //printf("%d %d</p><p>",k1,k2);
   i1= k1/n;
   j1= k1%n;
   i2= k2/n;
   j2= k2%n;
   arr[i1][j1]->endpoint= 1;
   arr[i2][j2]->path_number= ptno;
   arr[i1][j1]->path_number= ptno;
   node *n1, *n2;
   n1= arr[i1][j1];
   n2= arr[i2][j2];
   n1= findset(n1);
   n2= findset(n2);
   setunion(n1, n2);
   while(1) {
      i1= i2;
      j1= j2;
      k1= (i1*n)+j1;
      k2= valid_next(k1,n,arr);
      if(k2==-1) {
         arr[i1][j1]->endpoint= 1;
         break;
      }
      i2=k2/n;
      j2=k2%n;
      arr[i2][j2]->path_number= ptno;
      node *n1, *n2;
      n1= arr[i1][j1];
      n2= arr[i2][j2];
      n1= findset(n1);
      n2= findset(n2);
      setunion(n1,n2);
   }
   return 1;
}
void printtable(node ***arr, int n) {
   int i,j;
   printf("Table to be solved:</p><p>");
   for(i=0;i<n;i++) {
      for(j=0;j<n;j++) {
         if(arr[i][j]->endpoint ==1){
            if(arr[i][j]->path_number/10==0)
               printf("| %d |",arr[i][j]->path_number);
            else
               printf("| %d|",arr[i][j]->path_number);
         } else if(arr[i][j]->path_number==0)
            printf("| X |");
         else
            printf("| |");
      }
      printf("</p><p>");
   }
   printf("</p><p></p><p>The solution to the above table:</p><p>");
   for(i=0;i<n;i++) {
      for(j=0;j<n;j++) {
         if(arr[i][j]->path_number != 0){
            if(arr[i][j]->path_number/10==0)
               printf("| %d |",arr[i][j]->path_number);
            else
               printf("| %d|",arr[i][j]->path_number);
         } else
            printf("| X |");
      }
      printf("</p><p>");
   }
}
int main(void) {
   srand((unsigned int) time (NULL));
   int i, j;
   int ct = 1;
   int n = 7;
   node*** pointers= (node ***)malloc(n*sizeof(node **));
   for (i=0; i<n; i++)
      pointers[i] = (node **)malloc(n*sizeof(node *));
   initboard(pointers, n);
   while(1) {
      i = addpath(pointers, n, ct);
      if (i==0) {
         break;
      } else {
         ct++;
      }
   }
   printtable(pointers,n);
   return 0;
}

Atas ialah kandungan terperinci Permainan padanan nombor?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!