Bagaimana untuk melakukan ujian F dalam Python

Perangkawan menggunakan ujian F untuk menyemak sama ada dua set data mempunyai varians yang sama. Ujian-F dinamakan sempena Sir Ronald Fisher. Untuk menggunakan ujian-F, kami membuat dua hipotesis, hipotesis nol dan hipotesis alternatif. Kami kemudian memilih mana-mana daripada dua hipotesis yang disahkan oleh ujian F.

Variance ialah ukuran taburan data yang menerangkan sisihan data daripada min. Nilai yang lebih tinggi menunjukkan penyebaran yang lebih besar daripada nilai yang lebih kecil.

Dalam artikel ini, anda akan belajar cara melaksanakan F-Test dalam bahasa pengaturcaraan Python bersama-sama dengan kes penggunaannya.

Proses Pengujian F

Proses melakukan F-test adalah seperti berikut:

• Pertama, takrifkan hipotesis nol dan hipotesis alternatif.

• Hipotesis nol atau H0: σ12 = σ22 (Varian populasi sama)

• Hipotesis alternatif atau H1: σ12 ≠ σ22 (varian populasi tidak sama)

• Pilih statistik untuk ujian.

• Kira darjah kebebasan keseluruhan. Contohnya, jika m dan n ialah bentuk keseluruhan, darjah kebebasan dinyatakan sebagai (df1) = m–1 dan (df2) = n – 1 masing-masing.

• Sekarang cari nilai F daripada jadual F.

• Akhir sekali, bahagikan nilai alfa ujian dua hujung dengan 2 untuk mengira nilai kritikal.

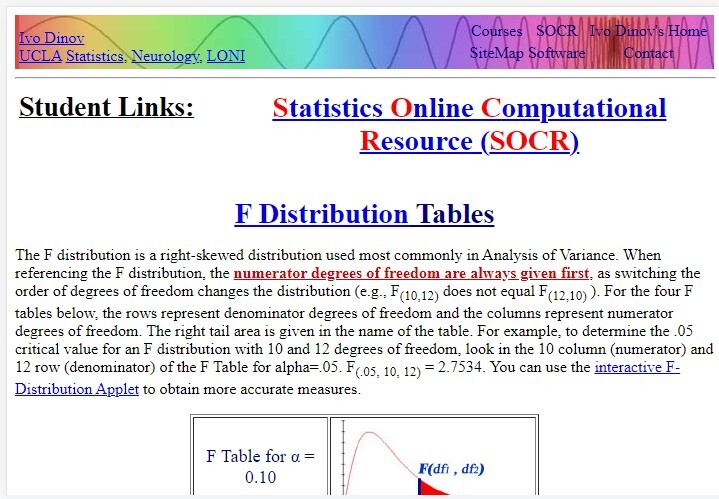
Oleh itu, kami mentakrifkan nilai F menggunakan darjah kebebasan populasi. Kami membaca df1 di baris pertama dan df2 di lajur pertama.

Terdapat pelbagai jadual F untuk darjah kebebasan yang unik. Kami membandingkan statistik F dari langkah 2 kepada nilai kritikal yang dikira dalam langkah 4. Jika nilai kritikal kurang daripada statistik F, kita boleh menolak hipotesis nol. Sebaliknya, apabila nilai kritikal lebih besar daripada statistik F pada beberapa tahap ketara, kita boleh menerima hipotesis nol.

Hipotesis

Sebelum menjalankan ujian-F berdasarkan set data, kami membuat beberapa andaian.

• Data secara amnya mematuhi taburan normal, iaitu, ia mematuhi lengkung berbentuk loceng.

• Tiada korelasi antara sampel, iaitu tiada multikolineariti dalam populasi.

Sebagai tambahan kepada andaian ini, kita juga harus mempertimbangkan perkara penting berikut semasa menjalankan ujian-F:

• Nilai varians maksimum hendaklah dalam pengangka untuk melakukan ujian ekor kanan.

• Dalam ujian dua hujung, bahagikan alfa dengan 2 untuk menentukan nilai kritikal.

• Semak sama ada terdapat varians atau sisihan piawai.

• Jika tiada darjah kebebasan dalam jadual F, nilai maksimum digunakan sebagai nilai kritikal.

Aplikasi F-Test dalam Python

Tatabahasa

scipy stats.f()

Parameter

x :  quantiles
q :  lower or upper tail probability
dfn, dfd shape parameters
loc :location parameter
scale :  scale parameter (default=1)
size :  random variate shape
moments : [‘mvsk’] letters, specifying which moments to compute

Terjemahan bahasa Cina bagi

Penjelasan

ialah:

Penjelasan

Dalam kaedah ini, pengguna mesti menghantar f_value dan panjang lelaran setiap tatasusunan kepada scipy.stats.f.cdf() dan tolak 1 daripadanya untuk melaksanakan ujian F.

Algoritma

• Mula-mula, import perpustakaan NumPy dan Scipy.stats untuk operasi.

• Kemudian buat dua senarai nilai yang dipilih secara rawak dengan dua nama pembolehubah berbeza, tukarkannya kepada tatasusunan NumPy dan gunakan Numpy untuk mengira varians setiap tatasusunan.

• Tentukan fungsi untuk mengira skor-F di mana mula-mula kita membahagikan varians tatasusunan dengan darjah kebebasan sebagai 1.

• Kemudian hitung panjang lelaran setiap tatasusunan dan hantar nilai-f (nisbah varians) dan panjang ke dalam fungsi CDF dan tolak panjang daripada 1 untuk mengira nilai-p.

• Akhir sekali, fungsi mengembalikan p_value dan f_value.

Contoh

import numpy as np
import scipy.stats

# Create data
group1 = [0.28, 0.2, 0.26, 0.28, 0.5]
group2 = [0.2, 0.23, 0.26, 0.21, 0.23]

# Converting the list to an array
x = np.array(group1)
y = np.array(group2)

# Calculate the variance of each group
print(np.var(group1), np.var(group2))

def f_test(group1, group2):
   f = np.var(group1, ddof=1)/np.var(group2, ddof=1)
   nun = x.size-1
   dun = y.size-1
   p_value = 1-scipy.stats.f.cdf(f, nun, dun)
   return f, p_value

# perform F-test
f_test(x, y)

Output

Variances: 0.010464 0.00042400000000000017

Anda boleh perhatikan bahawa nilai ujian-F ialah 4.38712 dan nilai p yang sepadan ialah 0.019127.

Memandangkan nilai-p kurang daripada 0.05, kami akan meninggalkan hipotesis nol. Oleh itu, kita boleh mengatakan bahawa varians kedua-dua populasi adalah tidak sama.

Kesimpulan

Selepas membaca artikel ini, anda kini tahu cara menggunakan ujian-F untuk menyemak sama ada dua sampel tergolong dalam populasi dengan varians yang sama. Anda telah mempelajari tentang prosedur ujian-F, andaian dan pelaksanaan Python. Mari kita akhiri artikel ini dengan beberapa perkara penting -

• Ujian-F memberitahu anda sama ada dua populasi mempunyai varians yang sama.

• Kira darjah kebebasan dan kira nilai kritikal.

• Cari statistik F dari jadual F dan bandingkan dengan nilai kunci yang dikira dalam langkah sebelumnya.

• Terima atau tolak hipotesis nol berdasarkan nilai kritikal dan perbandingan statistik F.

Atas ialah kandungan terperinci Bagaimana untuk melakukan ujian F dalam Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!