Rumah >Peranti teknologi >AI >Deep Thinking |. Di manakah sempadan keupayaan model besar?
Deep Thinking |. Di manakah sempadan keupayaan model besar?
- PHPzke hadapan
- 2023-09-08 17:41:051382semak imbas
Jika kita mempunyai sumber tanpa had, seperti data tak terhingga, kuasa pengkomputeran tak terhingga, model tak terhingga, algoritma pengoptimuman sempurna dan prestasi generalisasi, bolehkah model pra-latihan yang terhasil digunakan untuk menyelesaikan semua masalah?
Ini adalah soalan yang sangat dibimbangkan oleh semua orang, tetapi teori pembelajaran mesin sedia ada tidak dapat menjawabnya. Ia tidak ada kena mengena dengan teori kebolehan ekspresif, kerana model itu tidak terhingga dan kebolehan ekspresif secara semula jadi tidak terhingga. Ia juga tidak berkaitan dengan teori pengoptimuman dan generalisasi, kerana kami menganggap bahawa prestasi pengoptimuman dan generalisasi algoritma adalah sempurna. Dalam erti kata lain, masalah kajian teori terdahulu tidak lagi wujud di sini!
Hari ini, saya akan memperkenalkan kepada anda kertas kerja Mengenai Kuasa Model Asas yang saya terbitkan di ICML'2023, dan memberikan jawapan dari perspektif teori kategori.
Apakah itu teori kategori?
Jika anda bukan jurusan matematik, anda mungkin tidak biasa dengan teori kategori. Teori kategori dipanggil matematik matematik dan menyediakan bahasa asas untuk matematik moden. Hampir semua bidang matematik moden diterangkan dalam bahasa teori kategori, seperti topologi algebra, geometri algebra, teori graf algebra, dll. Teori kategori ialah kajian struktur dan hubungan Ia boleh dilihat sebagai lanjutan semula jadi teori set: dalam teori set, satu set mengandungi beberapa elemen yang berbeza dalam teori kategori, kita bukan sahaja merekodkan unsur-unsur, juga merekodkan hubungan antara unsur-unsur .
Martin Kuppe pernah melukis peta matematik, meletakkan teori kategori di bahagian atas peta, menyinari semua bidang matematik:
Terdapat banyak pengenalan kepada teori kategori di Internet. Mari kita bercakap secara ringkas tentang beberapa perkara konsep asas di sini:

Kategori teori perspektif pembelajaran diselia

Dalam sepuluh tahun yang lalu, orang ramai telah menjalankan banyak penyelidikan di sekitar kerangka pembelajaran yang diselia dan memperoleh banyak kesimpulan yang indah. Walau bagaimanapun, rangka kerja ini juga mengehadkan pemahaman orang tentang algoritma AI, menjadikannya amat sukar untuk memahami model pra-latihan yang besar. Sebagai contoh, teori generalisasi sedia ada sukar untuk menerangkan keupayaan pembelajaran silang mod model.

Bolehkah kita mempelajari functor ini dengan mengambil sampel data input dan outputnya?
Perhatikan bahawa dalam proses ini kami tidak mengambil kira struktur dalaman dua kategori X dan Y. Malah, pembelajaran yang diselia tidak membuat sebarang andaian tentang struktur dalam kategori, jadi boleh dianggap bahawa tidak ada hubungan antara mana-mana dua objek dalam dua kategori. Oleh itu, kita boleh menganggap X dan Y sebagai dua set. Pada masa ini, teorem tiada makan tengah hari percuma yang terkenal bagi teori generalisasi memberitahu kita bahawa tanpa andaian tambahan, adalah mustahil untuk mempelajari functor dari X hingga Y (melainkan jika terdapat sampel besar).

Pada pandangan pertama, perspektif baru ini tidak berguna. Sama ada menambah kekangan pada kategori atau menambah kekangan pada functors, nampaknya tiada perbezaan penting. Malah, perspektif baharu itu lebih seperti versi rangka kerja tradisional yang dikebiri: ia tidak menyebut konsep fungsi kehilangan, yang amat penting dalam pembelajaran diselia, dan tidak boleh digunakan untuk menganalisis sifat penumpuan atau generalisasi latihan. algoritma. Jadi bagaimana kita harus memahami perspektif baru ini?
Saya rasa teori kategori memberikan pandangan mata burung. Ia tidak dengan sendirinya dan tidak sepatutnya menggantikan rangka kerja pembelajaran diselia asal yang lebih khusus, atau digunakan untuk menghasilkan algoritma pembelajaran diselia yang lebih baik. Sebaliknya, rangka kerja pembelajaran yang diselia ialah "sub-modul", alat yang boleh digunakan untuk menyelesaikan masalah tertentu. Oleh itu, teori kategori tidak mengambil berat tentang fungsi kehilangan atau prosedur pengoptimuman - ini lebih seperti butiran pelaksanaan algoritma. Ia lebih memfokuskan pada struktur kategori dan functors, dan cuba memahami sama ada functor tertentu boleh dipelajari. Masalah ini amat sukar dalam rangka kerja pembelajaran tradisional yang diselia, tetapi menjadi lebih mudah dalam perspektif kategori. Perspektif teori kategori pembelajaran penyeliaan kendiri Sebenarnya, jika kita tidak mereka bentuk apa-apa tugasan pra-latihan, tidak akan ada hubungan antara objek dalam kategori tetapi selepas mereka bentuk tugasan pra-latihan, kita akan menyuntik pengetahuan sedia ada manusia ke dalam kategori dalam bentuk tugas.
Dan struktur ini menjadi pengetahuan yang dimiliki oleh model besar.Khususnya:

Dalam erti kata lain, selepas kami mentakrifkan tugas pra-latihan pada set data, kami mentakrifkan kategori yang mengandungi struktur perhubungan yang sepadan. Matlamat pembelajaran tugas pra-latihan adalah untuk membiarkan model mempelajari kategori ini dengan baik. Secara khusus, kita melihat konsep model yang ideal. Model ideal #
dipratakrifkan sebelum melihat data; tetapi subskrip f bermakna kedua-dua fungsi f danboleh digunakan melalui panggilan kotak hitam. Dalam erti kata lain,
ialah fungsi "mudah", tetapi boleh menggunakan keupayaan model f untuk mewakili perhubungan yang lebih kompleks. Ini mungkin tidak mudah difahami Mari kita gunakan algoritma pemampatan sebagai analogi. Algoritma pemampatan itu sendiri mungkin bergantung kepada data, contohnya ia mungkin dioptimumkan khas untuk pengedaran data. Walau bagaimanapun, sebagai fungsi bebas data  , ia tidak boleh mengakses pengedaran data, tetapi ia boleh memanggil algoritma mampatan untuk menyahmampat data, kerana operasi "memanggil algoritma mampatan" adalah bebas data .
, ia tidak boleh mengakses pengedaran data, tetapi ia boleh memanggil algoritma mampatan untuk menyahmampat data, kerana operasi "memanggil algoritma mampatan" adalah bebas data .
Untuk tugasan pra-latihan yang berbeza, kita boleh mentakrifkan : #🎜🎜🎜##🎜🎜 kita boleh katakan begini: Proses pembelajaran pra-latihan ialah proses mencari model yang ideal f.
Namun, walaupun adalah pasti, mengikut definisi, model yang ideal bukanlah unik. Secara teorinya, model f boleh menjadi sangat pintar dan boleh melakukan apa sahaja tanpa mempelajari data dalam C. Dalam kes ini, kita tidak boleh membuat kenyataan yang bermakna tentang keupayaan f . Oleh itu, kita harus melihat sisi lain masalah:
 Memandangkan kategori C yang ditakrifkan oleh tugas pra-latihan, untuk mana-mana f ideal, apakah tugas yang boleh diselesaikannya?
Memandangkan kategori C yang ditakrifkan oleh tugas pra-latihan, untuk mana-mana f ideal, apakah tugas yang boleh diselesaikannya?
Ini adalah soalan teras yang ingin kami jawab pada awal artikel ini. Mari kita perkenalkan konsep penting dahulu.
米田embed
###🎜🎜🎜##🎜🎜🎜🎜🎜🎜🎜 Mudah untuk membuktikan bahawa
adalah model ideal dengan keupayaan paling lemah, kerana memandangkan model ideal lain f, semua hubungan dalam
juga termasuk dalam f. Pada masa yang sama, ia juga merupakan matlamat utama pembelajaran model pra-latihan tanpa andaian tambahan lain. Oleh itu, untuk menjawab soalan teras kami, kami mempertimbangkan di bawah secara khusus .
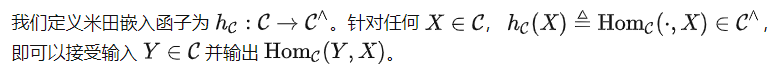 Penalaan segera: Hanya apabila anda melihat lebih banyak anda boleh belajar lebih lanjut
Penalaan segera: Hanya apabila anda melihat lebih banyak anda boleh belajar lebih lanjut

#🎜Can Do🎜 anda ingin menyelesaikan tugas tertentu T? Untuk menjawab soalan ini, kami mula-mula memperkenalkan salah satu teorem yang paling penting dalam teori kategori. Yoneda Yuri
Iaitu, Iaitu,
Iaitu, #🎜🎜 Gunakan dua perwakilan ini untuk mengira T(X). Walau bagaimanapun, perhatikan bahawa gesaan tugas P mesti dihantar melalui  bukannya
bukannya
, yang bermaksud kita akan mendapat
(P) dan bukannya T sebagai input. Ini membawa kepada satu lagi definisi penting dalam teori kategori.

Berdasarkan definisi ini, kita boleh mendapatkan teorem berikut (bukti dihilangkan). Teorem 1 dan AkibatAda beberapa petua untuk itu penalaan Petunjuk algoritma tidak semestinya objek dalam kategori C, tetapi mungkin merupakan perwakilan dalam ruang ciri. Pendekatan ini berpotensi untuk menyokong tugas yang lebih kompleks daripada tugas yang boleh diwakili, tetapi peningkatan bergantung pada kuasa ekspresif ruang ciri. Di bawah ini kami menyediakan akibat mudah Teorem 1.
Corollary 1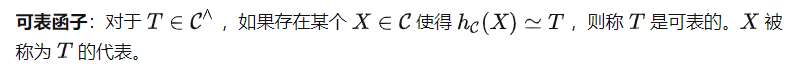 Untuk tugas pra-latihan meramal sudut putaran imej [4], penalaan segera tidak dapat menyelesaikan tugasan hiliran yang kompleks seperti pembahagian atau pengelasan.
Untuk tugas pra-latihan meramal sudut putaran imej [4], penalaan segera tidak dapat menyelesaikan tugasan hiliran yang kompleks seperti pembahagian atau pengelasan.
Bukti: Tugas pra-latihan untuk meramal sudut putaran imej memutarkan imej yang diberikan dengan empat sudut berbeza: 0°, 90°, 180° dan 270°, dan membolehkan model membuat ramalan. Oleh itu, kategori yang ditakrifkan oleh tugas pra-latihan ini meletakkan setiap objek ke dalam kumpulan 4 elemen. Jelas sekali, tugas seperti pembahagian atau pengelasan tidak boleh diwakili oleh objek mudah tersebut.
Corollary 1 agak intuitif sedikit, kerana kertas asal menyebut [4] bahawa model yang diperoleh menggunakan kaedah ini boleh menyelesaikan sebahagian tugas hiliran seperti klasifikasi atau segmentasi. Walau bagaimanapun, dalam definisi kami, menyelesaikan tugas bermakna model harus menjana output yang betul untuk setiap input, jadi sebahagiannya betul tidak dianggap sebagai kejayaan. Ini juga konsisten dengan soalan yang dinyatakan pada permulaan artikel kami: Dengan sokongan sumber tanpa had, bolehkah tugas pra-latihan untuk meramal sudut putaran imej digunakan untuk menyelesaikan tugas hiliran yang kompleks? Akibat 1 memberikan jawapan negatif.
Penalaan halus: Perwakilan tanpa kehilangan maklumat
Petua bahawa keupayaan untuk menala adalah terhad, jadi bagaimana pula dengan algoritma penalaan halus? Berdasarkan teorem pengembangan fungsi Yoneda (lihat Proposisi 2.7.1 dalam [5]), kita boleh memperoleh teorem berikut.
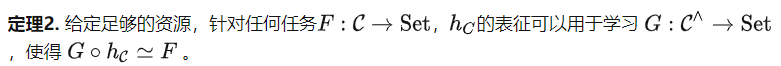
Teorem 2 mempertimbangkan tugas hiliran berdasarkan struktur C dan bukannya kandungan data dalam set data. Oleh itu, kategori yang ditakrifkan oleh tugas pra-latihan yang dinyatakan sebelum ini untuk meramalkan sudut imej yang diputar masih mempunyai struktur kumpulan yang sangat mudah. Tetapi menurut Teorem 2, kita boleh menggunakannya untuk menyelesaikan tugas yang lebih pelbagai. Sebagai contoh, kita boleh memetakan semua objek kepada output yang sama, yang tidak boleh dilakukan dengan penalaan petunjuk. Teorem 2 menjelaskan kepentingan tugas pra-latihan, kerana tugas pra-latihan yang lebih baik akan mewujudkan kategori C yang lebih berkuasa, sekali gus meningkatkan lagi potensi penalaan halus model.
Terdapat dua salah faham biasa tentang Teorem 2. Pertama sekali, walaupun kategori C mengandungi sejumlah besar maklumat, Teorem 2 hanya memberikan batas atas yang kasar, mengatakan bahawa merekodkan semua maklumat dalam C dan berpotensi untuk menyelesaikan sebarang tugas, tetapi ia tidak menyatakan bahawa sebarang algoritma penalaan halus boleh mencapai matlamat ini. Kedua, Teorem 2 kelihatan seperti teori overparameter pada pandangan pertama. Walau bagaimanapun, mereka menganalisis langkah-langkah pembelajaran yang diselia sendiri yang berbeza. Analisis parametrik ialah langkah pra-latihan, yang bermaksud bahawa di bawah andaian tertentu, selagi model itu cukup besar dan kadar pembelajaran cukup kecil, ralat pengoptimuman dan generalisasi akan menjadi sangat kecil untuk tugas pra-latihan. Teorem 2 menganalisis langkah penalaan halus selepas pra-latihan, mengatakan bahawa langkah ini mempunyai potensi yang besar.
Perbincangan dan rumusan
Pembelajaran penyeliaan dan pembelajaran penyeliaan sendiri. Dari perspektif pembelajaran mesin, pembelajaran penyeliaan sendiri masih merupakan jenis pembelajaran diselia, tetapi cara untuk mendapatkan label adalah lebih bijak. Tetapi dari perspektif teori kategori, pembelajaran penyeliaan kendiri mentakrifkan struktur dalam kategori, manakala pembelajaran diselia mentakrifkan hubungan antara kategori. Oleh itu, mereka berada di bahagian yang berlainan dalam peta kecerdasan buatan dan melakukan perkara yang sama sekali berbeza.

Senario yang boleh digunakan. Memandangkan andaian sumber yang tidak terhingga telah dipertimbangkan pada permulaan artikel ini, ramai rakan mungkin berfikir bahawa teori ini hanya boleh benar-benar ditubuhkan dalam kekosongan. Ini tidak berlaku. Dalam proses terbitan sebenar kami, kami hanya mempertimbangkan model ideal dan fungsi yang telah ditetapkan . Malah, selagi ditentukan, mana-mana model pra-latihan f (walaupun dalam peringkat permulaan rawak) boleh mengira f(X) untuk input XC, dan dengan itu menggunakan untuk mengira hubungan antara dua objek. Dalam erti kata lain, selagi ditentukan, setiap model pra-latihan sepadan dengan kategori, dan matlamat pra-latihan hanyalah untuk terus menyelaraskan kategori ini dengan kategori yang ditakrifkan oleh tugas pra-latihan . Oleh itu, teori kami berlaku untuk setiap model yang telah dilatih.
Formula teras. Ramai orang mengatakan bahawa jika AI benar-benar mempunyai satu set sokongan teori, maka harus ada satu atau beberapa formula ringkas dan elegan di belakangnya. Saya fikir jika formula teori kategori perlu digunakan untuk menggambarkan keupayaan model besar, ia sepatutnya seperti yang kami sebutkan sebelum ini:
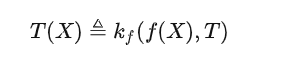
Untuk rakan-rakan yang biasa dengan model besar, selepas pemahaman yang mendalam tentang maksud formula ini, anda mungkin Anda mungkin berfikir bahawa formula ini adalah karut, tetapi ia hanya menyatakan mod kerja model besar semasa menggunakan formula matematik yang agak kompleks.
Tetapi bukan itu yang berlaku. Sains moden berasaskan matematik, dan matematik moden berdasarkan teori kategori, dan teorem yang paling penting dalam teori kategori ialah lemma Yoneda. Formula yang saya tulis membongkar isomorfisme Yoneda Lemma kepada versi asimetri, tetapi ia betul-betul sama dengan cara membuka model besar.
Saya rasa ini mesti bukan satu kebetulan. Jika teori kategori boleh menerangi pelbagai cabang matematik moden, ia juga boleh menerangi jalan ke hadapan untuk kecerdasan buatan am.
Artikel ini diilhamkan oleh kerjasama jangka panjang dan erat dengan pasukan Qianfang Institut Penyelidikan Kepintaran Buatan Beijing Zhiyuan.

Pautan asal: https://mp.weixin.qq.com/s/bKf3JADjAveeJDjFzcDbkw
Atas ialah kandungan terperinci Deep Thinking |. Di manakah sempadan keupayaan model besar?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

