Rumah >pembangunan bahagian belakang >C++ >nombor dodekagon pusat
nombor dodekagon pusat
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2023-09-07 12:09:021225semak imbas
Nombor grafik yang menggambarkan dodekagon dipanggil nombor dodekagon. Nombor dodekagon pusat diwakili oleh satu titik di tengah dan titik lain yang mengelilingi titik itu dalam lapisan dodekagon berterusan (iaitu, poligon 12 sisi).
Nombor dodekagon pusat boleh dijelaskan dengan lebih baik oleh imej di bawah.

Untuk n=1, hanya terdapat satu titik di tengah. Jadi keluarannya ialah 1.
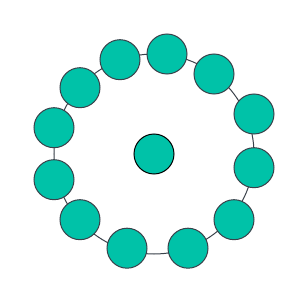
Untuk n=2, terdapat satu titik di tengah yang dikelilingi oleh dodekagon. Oleh itu, jumlah mata akan menjadi 13. Jadi nombor dodekagon pusat seterusnya ialah 13.
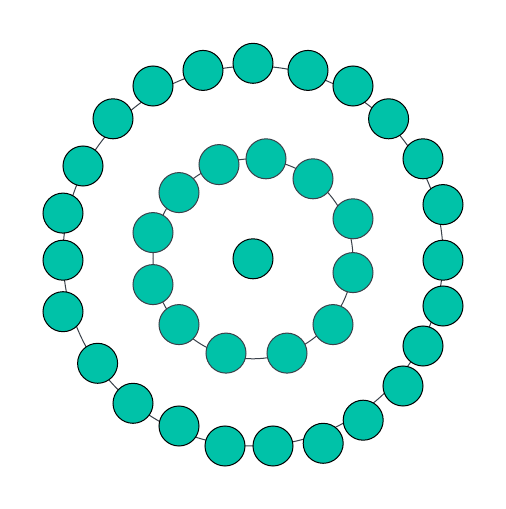
Untuk n=3, akan ada satu titik di tengah, diikuti dengan dodekagon mengelilinginya, dan kemudian lapisan berturut-turut dodekagon yang mengandungi 24 mata. Oleh itu, jumlah bilangan mata ialah 37, yang akan menjadi nombor dodekagon pusat seterusnya.
Begitu juga, ini mengikuti setiap nombor positif n. Merujuk kepada ini, beberapa nombor dodekagon pertama ialah 1, 13, 37, 73, 121, 181…..
Dalam masalah ini, kami akan diberikan sebarang nombor positif n dan perlu mencetak nombor dodekagon pusat ke-n.
Sebagai contoh,
Masuk - 2
Output - 13
Masuk - 5
Output - 121
Berikut ialah algoritma untuk menyelesaikan masalah ini.
Algoritma
Untuk mengira nombor dodekagon pusat ke-n, kita perlu memikirkan corak yang diikuti dalam masalah.
Mengikut konsep nombor dodekagon pusat, ia diwakili oleh titik di tengah dan kemudian lapisan dodekagon berturut-turut. Lapisan dodecagonal berturut-turut ialah 12, 24, 36, 48... Jika kita melihat dengan teliti pada corak, ia membentuk jujukan aritmetik dengan toleransi 12.
Memandangkan beberapa urutan pertama nombor dodekagon pusat ialah 1, 13, 37, 73…. Ia tidak lebih daripada jumlah lapisan dodekagon dan satu titik di tengah.
Kita boleh memahaminya dengan lebih baik jika kita mempertimbangkan urutan lapisan dodecagonal berturut-turut bermula dengan 0.
0, 12, 24, 36, 48. For n=1, the centred dodecagonal number is 1 which is 0+1. For n=2, the centred dodecagonal number is 13 which is 0+12+1. For n=3, the centred dodecagonal number is 37 which is 0+12+24+1.
Dari sini kita boleh berfikir bahawa nombor dodekagon pusat ke-n tidak lain adalah jumlah A.P. bagi n sebutan bermula dari 0 dengan toleransi ialah 12 dan 1.
Jadi formula nombor dodekagon pusat ke-n boleh dinyatakan sebagai,
$$mathrm{CDn=jujukan aritmetik (a=0: jumlah: d=12): daripada: hasil tambah n sebutan pertama: +1}$$
$$mathrm{CD_n:=:frac{n}{2}(2a:+:(n-1)d):+1}$$
Di sini, $mathrm{CD_n}$ ialah nombor dodekagon pusat ke-n
a ialah sebutan pertama bagi jujukan aritmetik, iaitu 0
d ialah toleransi bagi jujukan aritmetik, iaitu 12
Selanjutnya, formula boleh ditulis sebagai:
$$mathrm{CD_n:=:frac{12n}{2}(n-1):+:1}$$
$$mathrm{CD_n:=:6n(n-1):+:1}$$
Simpan teks asal tanpa terjemahanKami akan menggunakan formula di atas untuk mengira nombor dodekagon pusat ke-n dalam kaedah kami.
Kaedah
Untuk menyelesaikan masalah ini, kami hanya mencipta fungsi untuk mengira nombor dodekagon pusat ke-n.
Kami akan menggunakan formula terbitan di atas untuk mengira nombor dodekagon pusat ke-n untuk sebarang nombor positif.
Mengembalikan nilai yang dikira, yang akan menjadi output yang kita inginkan.
Contoh
ialah:Contoh
Berikut adalah pelaksanaan kaedah di atas dalam C++ -
#include <iostream>
#include<bits/stdc++.h>
using namespace std;
//function to calculate the nth centred dodecagonal number
int CDn(int N){
int ans= 6 * N * (N-1) + 1; //used to store nth centred dodecagonal number value
return ans; //return the answer
}
int main(){
int N=8;
cout<<CDn(N)<<endl;
N=6;
cout<<CDn(N)<<endl;
N=12;
cout<<CDn(N)<<endl;
return 0;
}
Output
337 181 793
Kerumitan masa: O(1), kerana masa yang berterusan diperlukan.
Kerumitan angkasa: O(1) kerana kami tidak menggunakan sebarang ruang tambahan.
Kesimpulan
Dalam artikel ini, kami menyelesaikan masalah mencetak nombor dodekagon berpusat ke-n. Kami mempelajari konsep nombor dodekagon berpusat dan memperoleh formula untuk nombor ke-n,
Saya harap anda mendapati artikel ini membantu dalam memahami dan menjelaskan semua konsep berkenaan isu ini.
Atas ialah kandungan terperinci nombor dodekagon pusat. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

