Visualisasikan O(n) menggunakan Python.

Pengenalan

Dalam bidang sains komputer dan pengaturcaraan, memahami kecekapan algoritma adalah penting kerana ia membantu mencipta perisian yang dioptimumkan dan berfungsi dengan cepat. Kerumitan masa ialah konsep penting dalam konteks ini kerana ia mengukur cara masa berjalan sesuatu algoritma berubah apabila saiz input bertambah. Kelas kerumitan masa yang biasa digunakan O(n) mewakili hubungan linear antara saiz input dan masa pelaksanaan.

Definisi

Kerumitan algoritma dalam sains komputer ialah penilaian sumber yang diperlukan, seperti penggunaan masa dan ruang, berdasarkan saiz input algoritma. Tambahan pula, ia menyokong pemahaman kita tentang kepantasan prestasi algoritma apabila saiz inputnya diambil kira. Notasi utama yang digunakan untuk menggambarkan kerumitan algoritma ialah notasi Big O (O(n)).

tatabahasa

for i in range(n):
   # do something

Gelung `untuk` menjalankan set arahan khusus berdasarkan julat dari 0 hingga `n-1` dan melaksanakan operasi atau set operasi pada setiap lelaran. di mana 'n' mewakili bilangan lelaran.

Di bawah kerumitan masa O(n), apabila saiz input 'n' meningkat, masa pelaksanaan meningkat secara berkadar. Apabila 'n' bertambah, bilangan lelaran gelung dan masa yang diperlukan untuk melengkapkan gelung akan meningkat secara berkadar. Kerumitan masa linear mempamerkan hubungan berkadar langsung antara saiz input dan masa pelaksanaan.

Sebarang tugasan atau urutan tugasan boleh dilaksanakan dalam gelung tanpa mengira saiz input 'n'. Aspek utama yang perlu diperhatikan di sini ialah gelung melaksanakan lelaran 'n', menghasilkan kerumitan masa linear.

Algoritma

• Langkah 1: Mulakan jumlah berubah menjadi 0

• Langkah 2: Lelaran melalui setiap elemen dalam senarai yang disediakan

• Langkah 3: Gabungkan elemen ke dalam nilai jumlah semasa.

• Langkah 4: Jumlah hendaklah dikembalikan selepas gelung tamat.

• Langkah 5: Tamat

kaedah

• Kaedah 1: Hubungan antara masa lukisan dan saiz input

• Kaedah 2: Hubungan antara operasi lukisan dan skala input

Kaedah 1: Lakarkan hubungan antara masa dan saiz input

Contoh

import time
import matplotlib.pyplot as plt

def algo_time(n):
    sum = 0
    for i in range(n):
        sum += i
    return sum

input_sizes = []
execution_times = []

for i in range(1000, 11000, 1000):
    start_time = time.time()
    algo_time(i)
    end_time = time.time()
    input_sizes.append(i)
    execution_times.append(end_time - start_time)

plt.plot(input_sizes, execution_times)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (s)')
plt.show()

Output

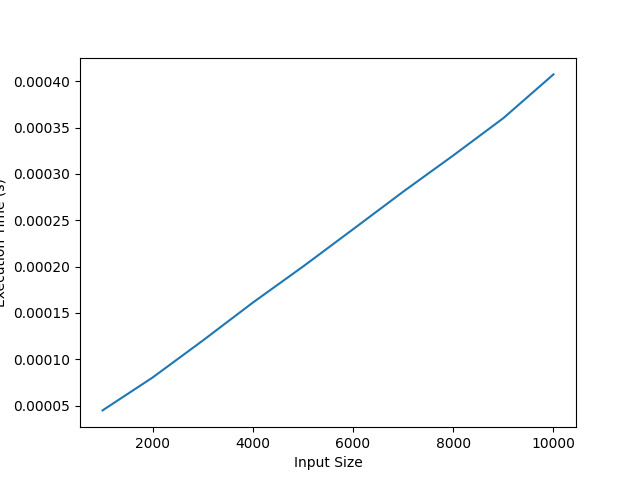
Kod ini digunakan untuk mengukur masa berjalan algoritma `algo_time()` di bawah saiz input yang berbeza. Kami akan menyimpan saiz input yang ingin kami uji dan masa pelaksanaan yang sepadan dalam senarai ini.

Gunakan gelung 'untuk' untuk lelaran pada julat saiz input. Dalam kes ini, gelung akan berjalan dari 1000 hingga lebih dekat kepada 11000, meningkat sebanyak 1000 setiap kali. Untuk menggambarkan lebih lanjut, kami merancang untuk menilai algoritma dengan mengubah nilai 'n' dari 1000 hingga 10000 dalam kenaikan 1000.

Di dalam gelung, kami mengukur masa pelaksanaan fungsi `algo_time()` untuk setiap saiz input. Untuk mula menjejak masa, kami menggunakan `time.time()` sebelum memanggil fungsi dan menghentikannya sebaik sahaja fungsi selesai berjalan. Kami kemudiannya menyimpan tempoh dalam pembolehubah yang dipanggil 'execution_time'.

Kami menambah setiap nilai input untuk saiz input tertentu ('n') dan masa pelaksanaan yang sepadan dengan senarai masing-masing ('saiz_input' dan 'masa_pelaksanaan').

Selepas gelung selesai, kami mempunyai data yang kami perlukan untuk menjana plot. 'plt.plot(input_sizes, execution_times)' menjana carta garis asas menggunakan data yang kami kumpulkan. Paksi-x menunjukkan nilai 'input_sizes' mewakili saiz input yang berbeza.

'plt.xlabel()' dan 'plt.ylabel()' akhirnya digunakan untuk menandakan makna paksi koordinat masing-masing, dan memanggil fungsi 'plt.show()' membolehkan kami mempersembahkan grafik.

Dengan menjalankan kod ini, kita boleh menggambarkan peningkatan dalam masa pelaksanaan apabila saiz input ('n') meningkat dengan memplot graf. Dengan mengandaikan bahawa kerumitan masa algoritma ialah O(n), kita boleh menganggarkan bahawa terdapat korelasi hampir garis lurus antara saiz input dan masa pelaksanaan semasa memplot graf.

Kaedah 2: Hubungan antara operasi lukisan dan saiz input

Contoh

import matplotlib.pyplot as plt

def algo_ops(n):
    ops = 0
    sum = 0
    for i in range(n):
        sum += i
        ops += 1
    ops += 1  # for the return statement
    return ops

input_sizes = []
operations = []

for i in range(1000, 11000, 1000):
    input_sizes.append(i)
    operations.append(algo_ops(i))

plt.plot(input_sizes, operations)
plt.xlabel

plt.xlabel('Input Size')
plt.ylabel('Number of Operations')
plt.show()

Output

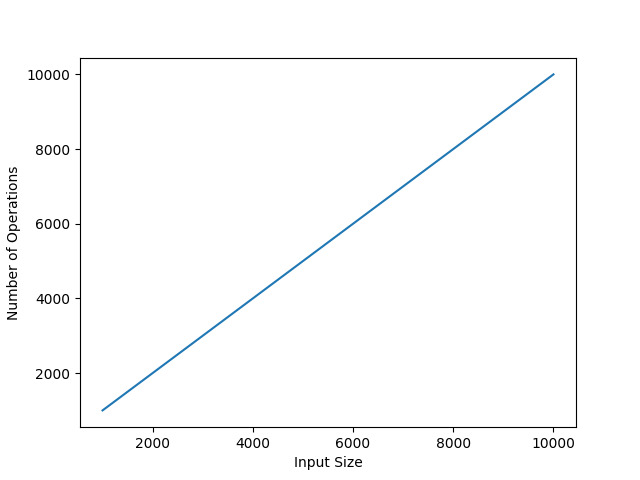
Kod ini direka untuk menganalisis bilangan operasi yang dilakukan oleh algoritma `algo_ops()` di bawah saiz input yang berbeza. Dengan menggunakan fungsi `algo_ops()`, anda boleh mengira jumlah semua nilai dalam julat dari sifar hingga parameter input 'n' yang diberikan, sambil menjejak dan merekod setiap operasi yang dilakukan semasa setiap pengiraan secara serentak.

Kami mula-mula mengimport modul 'matplotlib.pyplot', yang membolehkan kami membuat visualisasi seperti graf.

Seterusnya, kami mentakrifkan fungsi algo_ops(), yang menerima nombor input 'n'. Di dalam fungsi, kami memulakan dua pembolehubah: 'ops' untuk mengira bilangan operasi, dan 'sum' untuk menyimpan jumlah kumulatif nombor.

Tatasusunan ini akan menyimpan dimensi yang ingin kami periksa dan tempoh pelaksanaan yang sepadan.

Salah satu cara kami menggunakan gelung berulang ialah dengan menggelung pada berbilang skala input. Dalam kes ini, julat pelaksanaan gelung adalah dari 1000 hingga 10000 (kecuali 11000). Ini bermakna kita akan menilai teknik dengan pembolehubah 'n' antara 1000 dan 10000 dalam kenaikan 100.

Dalam gelung, kami mengira prestasi proses `algo_time()` untuk semua saiz input. Kami menggunakan `time.time()` untuk memulakan jam randik sebelum memanggil prosedur dan menamatkannya terus selepas subrutin selesai melaksanakan. Seterusnya, kami menyimpan selang masa dalam pembolehubah yang dipanggil 'execution_period'.

Untuk setiap saiz input, kami memasukkan nilai input ('n') dalam senarai yang dipanggil 'input_sizes'. Selain itu, kami menambahkan masa pemprosesan yang sepadan dalam koleksi 'execution_times'.

Selepas gelung selesai, kami telah mengumpul data asas yang diperlukan untuk membuat carta. Pernyataan 'plt.plot(input_sizes, execution_times)' mencipta carta garis asas menggunakan data yang dikumpul. Nilai 'input_sizes' ditunjukkan pada paksi-x dan mewakili saiz input yang berbeza. Nilai 'execution_times' ditunjukkan pada paksi menegak dan mewakili masa yang diperlukan untuk melaksanakan fungsi `algo_time()` dengan saiz input yang berbeza-beza.

Akhir sekali, kami melabel sistem koordinat melalui 'plt.xlabel()' dan 'plt.ylabel()' untuk menunjukkan maksud setiap paksi. Seterusnya, laksanakan fungsi 'plt.show()' untuk menghasilkan graf.

Sebaik sahaja kami melaksanakan program, graf akan menunjukkan kepada kami bagaimana masa pemprosesan meningkat apabila saiz input ('n') berkembang.

Kesimpulan

Ringkasnya, menguasai kerumitan masa dan visualisasi dalam Python menggunakan Matplotlib ialah kemahiran yang berharga untuk mana-mana pengaturcara yang ingin mencipta penyelesaian perisian yang cekap dan dioptimumkan. Memahami cara algoritma berkelakuan pada skala input yang berbeza membolehkan kami menyelesaikan masalah yang kompleks dan membina aplikasi teguh yang memberikan hasil tepat pada masanya dan cekap.

Atas ialah kandungan terperinci Visualisasikan O(n) menggunakan Python.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!