Menyemak sama ada graf yang dibina daripada tatasusunan berdasarkan keadaan tertentu mengandungi kitaran

Pengenalan

Dalam teori graf, adalah tugas yang sangat penting untuk mengetahui sama ada graf yang dibina daripada tatasusunan dan memenuhi syarat tertentu mempunyai kitaran. Gambar rajah ialah cara imaginatif untuk menunjukkan bagaimana sesuatu disambungkan. Ia digunakan di banyak tempat, seperti rangkaian komputer dan rangkaian sosial. Artikel ini membincangkan syarat untuk pembinaan graf, algoritma BFS dan DFS serta memberikan arahan langkah demi langkah tentang cara mengenal pasti kitaran dalam graf tidak terarah.

Perwakilan tatasusunan graf

Kaedah berasaskan tatasusunan dalam teori graf menyimpan bucu dan tepi dalam tatasusunan, yang menjadikannya mudah untuk digunakan dan digunakan dalam algoritma. Bermula dengan graf kosong, menambah bucu dan tepi satu demi satu berdasarkan maklumat dalam tatasusunan adalah asas untuk penerokaan selanjutnya, seperti pengesanan kitaran, yang penting untuk memahami cara graf dipautkan dan sama ada terdapat kitaran.

Graf keadaan pembinaan

Penjelasan syarat yang diberikan

• Graf dibina daripada tatasusunan, dengan tatasusunan mewakili set bucu dan sambungan atau tepinya.

• Setiap elemen tatasusunan sepadan dengan bucu dalam graf

• Nilai setiap elemen dalam tatasusunan mewakili indeks bucu yang disambungkannya (bucu jirannya).

• Indeks tatasusunan mewakili bucu itu sendiri, dan nilai sepadannya mewakili bucu ia disambungkan.

Syarat untuk mengesahkan pembinaan graf

• Semak sama ada tatasusunan itu sah dan memenuhi syarat yang diperlukan sebelum membina carta.

• Pastikan tatasusunan tidak kosong dan mengandungi sekurang-kurangnya satu elemen untuk mencipta bucu.

• Sahkan bahawa tatasusunan hanya mengandungi integer bukan negatif, kerana nilai negatif atau data tidak sah tidak boleh mewakili bucu atau tepi yang sah

• Pastikan indeks tatasusunan berada dalam julat yang sesuai. Mereka harus bermula dari 0 dan pergi ke n-1, di mana n ialah jumlah bilangan bucu dalam graf.

• Sahkan bahawa nilai (sambungan) dalam tatasusunan juga berada dalam julat sah 0 hingga n-1, pastikan ia sepadan dengan bucu sedia ada

• Semak sambungan pendua atau gelung kendiri kerana ia melanggar syarat untuk graf yang sah

• Sahkan bahawa tiada sambungan yang hilang, bermakna semua bucu disambungkan untuk membentuk graf lengkap atau komponen yang disambungkan

Algoritma DFS dan BFS

• Depth First Search (DFS) digunakan untuk meneroka bucu dan tepi graf dengan pergi sedalam setiap cabang yang mungkin sebelum berpusing

pseudokod

procedure DFS(graph, start_vertex, visited)
   if start_vertex is not in visited:
      mark start_vertex as visited
      process start_vertex (e.g., check for cycles)
      for each neighbor in graph[start_vertex]:
      if neighbor is not in visited:
      DFS(graph, neighbor, visited)
   end if
end procedure
    pocedure DFS_Traversal(graph)
    visited = empty set
      for each vertex in graph:
      if vertex is not in visited:
         DFS(graph, vertex, visited)
   end for
end procedure

• Breadth-first search (BFS) ialah algoritma traversal graf yang merentasi semua bucu graf satu lapisan pada satu masa. Ini menjadikannya cara yang bagus untuk mencari kitaran dalam carta

pseudokod

procedure BFS(graph, start_vertex):
   create an empty queue Q
   create a set visited to keep track of visited vertices
   
   enqueue start_vertex into Q
   add start_vertex to visited set
   
   while Q is not empty:
      current_vertex = dequeue from Q
      for each neighbor_vertex of current_vertex:
         if neighbor_vertex is not in visited set:
            enqueue neighbor_vertex into Q
            add neighbor_vertex to visited set
      else:
         // A cycle is detected, return true
         return true
      // No cycle found, return false
      return false

Kerumitan

• Kerumitan masa

Kerumitan masa kedua-dua BFS dan DFS ialah O(V + E), dengan V ialah bilangan bucu dan E ialah bilangan tepi.

• Kerumitan ruang

Kerumitan masa BFS dan DFS ialah O(V).

Proses pengesanan kitaran langkah demi langkah

Mari kita pertimbangkan contoh dengan gambar rajah

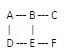
• Mulakan dari set kosong untuk memantau bucu yang dilawati

Visited set: {}

• Pilih mana-mana bucu sebagai titik permulaan untuk proses pengesanan gelung. Kami memilih bucu A.

Visited set: {A}
Current Vertex: A

• Periksa bucu bersebelahan bucu semasa (A). Dalam contoh ini, jiran A ialah B dan D. Tambahkannya pada set akses dan kenal pasti A sebagai nod induknya

Visited set: {A, B, D}
Current Vertex: A
Parent of B: A
Parent of D: A

• B ialah puncak yang dilawati seterusnya dalam set yang dilawati.

Visited set: {A, B, D}
Current Vertex: B
Parent of B: A

• Teroka persekitaran B. Jiran terdekat B ialah A, C dan E. A sudah berada dalam set puncak yang dilawati, tetapi ia bukan induk kepada B dan oleh itu tidak membentuk kitaran.

Visited set: {A, B, D, C, E}
Current Vertex: B

• Teruskan ke puncak yang dilawati seterusnya, iaitu D.

Visited set: {A, B, D, C, E}
Current Vertex: D
Parent of D: A

• Terjumpa kenalan D. A dan E ialah jiran terdekat D. Memandangkan A sudah termasuk dalam set akses dan merupakan induk kepada D, mesti ada tepi (D -> A) yang menyambungkan D kepada induknya. Ini menunjukkan bahawa graf mengandungi kitaran.

Cycle detected! There is an edge (D -> A) forming a cycle

Proses berakhir di sini, kami telah berjaya mengesan gelung dalam graf menggunakan BFS Iaitu (A->B->E->D->A).

Kesimpulan

Ringkasnya, untuk kebanyakan aplikasi adalah penting untuk dapat mencari kitaran dalam graf yang dibina daripada tatasusunan berdasarkan parameter yang diberikan. Sama ada anda menggunakan DFS atau BFS, proses ini membantu mencari kemungkinan gelung dan menyelesaikan masalah dunia sebenar yang melibatkan rangkaian, litar dan perhubungan. Pengesanan gelung yang berkesan boleh meningkatkan kelajuan algoritma anda dan memastikan data anda betul.

Atas ialah kandungan terperinci Menyemak sama ada graf yang dibina daripada tatasusunan berdasarkan keadaan tertentu mengandungi kitaran. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!