Analisis regresi dan garis lurus paling sesuai menggunakan Python

Dalam tutorial ini, kami akan melaksanakan analisis regresi dan garisan paling sesuai menggunakan pengaturcaraan Python

Pengenalan

Analisis regresi ialah bentuk analisis ramalan yang paling asas.

Dalam statistik, regresi linear ialah kaedah memodelkan hubungan antara nilai skalar dan satu atau lebih pembolehubah penjelasan.

Dalam pembelajaran mesin, regresi linear ialah algoritma yang diselia. Algoritma ini meramalkan nilai sasaran berdasarkan pembolehubah bebas.

Maklumat lanjut tentang regresi linear dan analisis regresi

Dalam regresi/analisis linear, sasaran adalah nilai sebenar atau berterusan seperti gaji, BMI, dll. Ia sering digunakan untuk meramalkan hubungan antara pembolehubah bersandar dan satu set pembolehubah tidak bersandar. Model ini biasanya sesuai dengan persamaan linear, walau bagaimanapun, terdapat jenis regresi lain, termasuk polinomial tertib tinggi.

Sebelum memasang model linear pada data, adalah perlu untuk menyemak sama ada terdapat hubungan linear antara titik data. Ini terbukti dari plot taburan mereka. Matlamat algoritma/model adalah untuk mencari garisan yang paling sesuai.

Dalam artikel ini, kami akan meneroka analisis regresi linear dan pelaksanaannya menggunakan C++.

Persamaan regresi linear adalah dalam bentuk Y = c + mx, di mana Y ialah pembolehubah sasaran dan X ialah pembolehubah bebas atau parameter/pembolehubah penerangan. m ialah kecerunan garis regresi dan c ialah pintasan. Memandangkan ini adalah tugas regresi 2D, model cuba mencari garisan yang paling sesuai semasa latihan. Semua mata tidak perlu berbaris tepat pada baris yang sama. Sesetengah titik data mungkin terletak pada baris, dan beberapa mungkin bertaburan di seluruh baris. Jarak menegak antara garis dan titik data ialah baki. Nilai boleh menjadi negatif atau positif bergantung pada sama ada titik di bawah atau di atas garisan. Baki ialah ukuran sejauh mana garisan itu sesuai dengan data. Algoritma ini berterusan untuk meminimumkan jumlah baki.

Baki bagi setiap pemerhatian ialah perbezaan antara nilai ramalan y (pembolehubah bersandar) dan nilai pemerhatian y

$$mathrm{baki: =:sebenar:y:nilai:−:ramalan:y:nilai}$$

$$mathrm{ri:=:yi:−:y'i}$$

Metrik yang paling biasa untuk menilai prestasi model regresi linear dipanggil ralat purata kuasa dua punca, atau RMSE. Idea asas adalah untuk mengukur sejauh mana ramalan model yang buruk/salah dibandingkan dengan pemerhatian sebenar.

Jadi, RMSE tinggi adalah "buruk" dan RMSE rendah adalah "baik"

Ralat RMSE ialah

$$mathrm{RMSE:=:sqrt{frac{sum_i^n=1:(this:-:this')^2}{n}}}$$ p>

RMSE ialah punca bagi min kuasa dua bagi semua baki.

Dilaksanakan menggunakan Python

Contoh

# Import the libraries
import numpy as np
import math
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Generate random data with numpy, and plot it with matplotlib:
ranstate = np.random.RandomState(1)
x = 10 * ranstate.rand(100)
y = 2 * x - 5 + ranstate.randn(100)
plt.scatter(x, y);
plt.show()

# Creating a linear regression model based on the positioning of the data and Intercepting, and predicting a Best Fit:
lr_model = LinearRegression(fit_intercept=True)
lr_model.fit(x[:70, np.newaxis], y[:70])
y_fit = lr_model.predict(x[70:, np.newaxis])

mse = mean_squared_error(y[70:], y_fit)
rmse = math.sqrt(mse)

print("Mean Square Error : ",mse)
print("Root Mean Square Error : ",rmse)

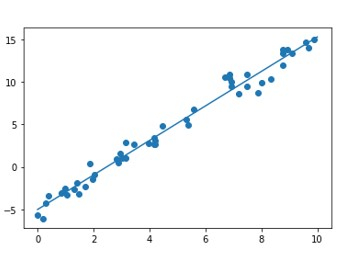
# Plot the estimated linear regression line using matplotlib:
plt.scatter(x, y)
plt.plot(x[70:], y_fit);
plt.show()

Output

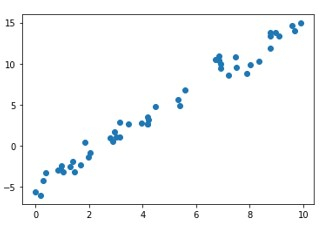
Mean Square Error : 1.0859922470998231 Root Mean Square Error : 1.0421095178050257

Kesimpulan

Analisis regresi ialah teknik yang sangat mudah tetapi berkuasa yang digunakan untuk analisis ramalan dalam pembelajaran mesin dan statistik. Idea ini terletak pada kesederhanaannya dan hubungan linear yang mendasari antara pembolehubah bebas dan sasaran.

Atas ialah kandungan terperinci Analisis regresi dan garis lurus paling sesuai menggunakan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!