Bilangan laluan dari akar ke daun dengan paling banyak M nod berturut-turut dan nilai K

Pengenalan

Pokok binari ialah struktur data yang menarik dengan pelbagai aplikasi dalam sains komputer dan pengaturcaraan. Masalah yang menarik ialah mencari kiraan daripada pokok tertentu yang terdiri daripada nod induk dan anak-anaknya. Pokok binari terdiri daripada nod, nod akar ditentukan, dan nod akar boleh menyediakan nod anak mengikut keperluan pengguna. Nilai K ditentukan, dan kaedah pergerakan dipilih oleh nilai M.

Bilangan laluan akar ke daun

Graf dibuat menggunakan pelbagai nod yang memegang nilai dalam bentuk integer. Artikel ini tertumpu terutamanya pada pengiraan daripada nod permulaan atau nod akar kepada nod daun atau nod anak.

Contoh

Graf dicipta daripada pokok binari dengan pelbagai nod.

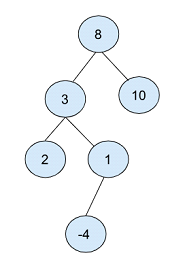
• Dalam pokok binari di atas, nod akar dipilih sebagai "8".

• Kemudian buat dua nod, satu dengan nilai 3 dan satu lagi dengan nilai 10, menduduki kedudukan kiri dan kanan nod akar.

• Mengambil nod dengan nilai 2 sebagai punca, cipta satu lagi nod anak dengan nilai 2 dan 1 sebagai nod kiri dan kanan masing-masing.

• Akhir sekali, nod anak dengan nilai 1 mencipta nod anak dengan nilai -4.

Kaedah 1: Kod C++ untuk mengira laluan akar ke daun yang terdiri daripada sehingga M nod berturut-turut dengan nilai K menggunakan fungsi rekursif

Untuk menyelesaikan masalah ini dengan cekap, kami akan menggunakan konsep asas seperti algoritma traversal pokok dan rekursi.

Algoritma

Langkah 1: Buat struktur untuk mewakili nod pokok, yang merangkumi dua penunjuk (nod anak kiri dan nod anak kanan) dan medan integer untuk menyimpan nilai nod.

Langkah 2: Reka fungsi rekursif untuk melintasi pokok binari bermula dari akar, sambil menjejaki panjang laluan semasa (dimulakan kepada 0), bilangan kejadian berturut-turut (pada mulanya ditetapkan kepada 0), nilai sasaran K, dan bilangan maksimum kejadian berturut-turut yang dibenarkan M .

Langkah 3: Panggil fungsi secara rekursif pada setiap subpokok kiri dan kanan, menghantar parameter yang dikemas kini seperti panjang laluan tambahan dan bilangan kejadian berturut-turut (jika berkenaan).

Langkah 4: Untuk setiap nod tidak kosong yang dilawati semasa traversal:

a) Jika nilainya sama dengan K, tambah satu pada kedua-dua pembolehubah.

b) Tetapkan semula pembolehubah kepada sifar jika nilainya tidak sepadan dengan K atau melebihi bilangan kejadian berturut-turut M yang telah ditemui setakat ini dalam laluan.

Langkah 5: Semasa melintasi pokok, jika nilai nod anak adalah sifar dalam kedua-dua kes kiri dan kanan - kita boleh mengendalikannya dalam dua cara, i.e.

a) Semak sama ada pembolehubah tidak melebihi M.

b) Jika ya, tambahkan jumlah laluan yang memenuhi syarat sebanyak 1.

Contoh

//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
   int data;
   struct Vertex* up;
   struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int 
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
   if (end == NULL || consCount > M) {
      return 0;
   }
//To check when the root is equal to the K value, increment by 1
   if (end->data == K) {
      currCount++;
      consCount++;
   } else {
//If it is not equal, it will return 0
      currCount = 0;
   }
   if (end->up == NULL && end->down == NULL) {
      if (currCount <= M) {
         return 1;
      } else {
         return 0;
      }
   }
   return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
   Vertex* end = new Vertex();
   end->data = 8;
   end->up = new Vertex();
   end->up->data = 3;
   end->down = new Vertex();
   end->down->data = 10;
   end->up->up = new Vertex();
   end->up->up->data = 2;
   end->up->down = new Vertex();
   end->up->down->data = 1;
   end->up->down->up = new Vertex();
   end->up->down->up->data = -4;

   int K = 1; // Value of node
   int M = 2; // Maximum consecutive nodes
   int currCount = -1; // Current count
   int consCount = -1; // Consecutive count

   cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;

   return 0;
} 

Output

The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3

Kesimpulan

Dalam artikel ini, kami meneroka masalah mengira bilangan laluan dari atas (iaitu daun) ke hujung atau akar. Masalah sedemikian boleh diselesaikan dengan cekap dengan menggunakan algoritma traversal pokok dan teknik rekursif dalam C++. Proses melintasi pokok binari mungkin kelihatan sukar, tetapi ia menjadi mudah dengan contoh.

Atas ialah kandungan terperinci Bilangan laluan dari akar ke daun dengan paling banyak M nod berturut-turut dan nilai K. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!