Rumah >Java >javaTutorial >Gunakan setiap hari! Adakah anda tahu apa itu HASH?
Gunakan setiap hari! Adakah anda tahu apa itu HASH?
- Java学习指南ke hadapan
- 2023-07-26 14:47:45723semak imbas
Pernahkah anda menggunakan HashMap? Jadi adakah anda benar-benar faham apa itu Hash? Artikel ini akan membawa anda melalui kajian mendalam tentang algoritma Hash dari peringkat prinsip.
1. Konsep pencincangan
Idea utama kaedah pencincangan adalah untuk menentukan alamat storan berdasarkan nilai kod kunci nod: mengambil nilai kod kunci K sebagai pembolehubah bebas, melalui perhubungan fungsi tertentu h(K ) (dipanggil fungsi cincang), kira nilai fungsi yang sepadan, tafsirkan nilai ini sebagai alamat storan nod dan simpan nod dalam unit storan ini. Apabila mendapatkan semula, gunakan kaedah yang sama untuk mengira alamat, dan kemudian pergi ke unit yang sepadan untuk mendapatkan nod yang anda cari. Nod boleh diperoleh dengan cepat melalui pencincangan. Hash (juga dipanggil "hash") ialah kaedah penyimpanan penting dan kaedah perolehan semula biasa.
Struktur storan yang dibina mengikut kaedah storan hash dipanggil jadual hash. Kedudukan dalam jadual cincang dipanggil slot. Teras teknologi pencincangan ialah fungsi pencincangan. Untuk mana-mana jadual carian dinamik DL, jika fungsi cincang "ideal" h dan HT jadual cincang yang sepadan dipilih, maka bagi setiap elemen data X dalam DL. Nilai fungsi h (kunci X) ialah lokasi penyimpanan X dalam jadual cincang HT. Elemen data X akan diletakkan pada kedudukan ini apabila memasukkan (atau membuat jadual), dan juga akan dicari pada kedudukan ini apabila mendapatkan semula X. Lokasi storan yang ditentukan oleh fungsi cincang dipanggil alamat cincang. Oleh itu, teras pencincangan ialah: fungsi cincang menentukan hubungan yang sepadan antara nilai kod kunci (X.key) dan alamat cincang h (X.key) Melalui perhubungan ini, penyimpanan dan pengambilan organisasi direalisasikan.
Secara amnya, ruang storan jadual cincang ialah tatasusunan satu dimensi HT[M] dan alamat cincang ialah subskrip tatasusunan. Matlamat mereka bentuk kaedah pencincangan adalah untuk mereka bentuk fungsi cincang tertentu h, 0<=h(K) Dalam perbincangan berikut, kami mengandaikan bahawa kami berurusan dengan kod utama yang nilainya adalah integer. supaya Tukarkan pengambilan kunci kepada pengambilan semula integer positif yang sepadan pada masa yang sama, selanjutnya diandaikan bahawa nilai fungsi cincang jatuh antara 0 dan M-1. Prinsip untuk memilih fungsi cincang adalah: operasi adalah semudah mungkin; julat nilai fungsi mestilah dalam skop jadual cincangan harus diedarkan sekata mungkin, iaitu, cuba buat berbeza kunci mempunyai nilai fungsi cincang yang berbeza. Pelbagai faktor perlu dipertimbangkan: panjang kunci, saiz jadual cincang, pengedaran kunci, kekerapan pengambilan rekod, dsb. Di bawah ini kami memperkenalkan beberapa fungsi cincang yang biasa digunakan. Seperti namanya, kaedah selebihnya ialah membahagikan kod kunci x dengan M (selalunya mengambil panjang jadual cincang), dan mengambil baki sebagai alamat cincang. Kaedah selebihnya ialah kaedah pencincangan yang paling mudah, dan fungsi cincang ialah: h(x) = x mod M. Apabila menggunakan kaedah ini, darabkan kod kunci dengan pemalar A (0< A < 1), dan ekstrak bahagian perpuluhan hasil. Kemudian, darabkan nilai ini dengan integer n, bundarkan ke bawah hasilnya dan gunakannya sebagai alamat cincang. Fungsi cincang ialah: cincang (kunci) = _LOW(n × (A × kunci % 1)). Antaranya, "A × kunci % 1" bermaksud mengambil bahagian perpuluhan kunci A ×, iaitu: A × kunci % 1 = A × kunci - _LOW(A × kunci), dan _LOW(X) bermaksud mengambil bahagian integer daripada X Memandangkan pembahagian integer biasanya berjalan lebih perlahan daripada pendaraban, secara sedar mengelak penggunaan operasi yang selebihnya boleh meningkatkan masa berjalan algoritma cincang. Pelaksanaan khusus kaedah persegi-tengah adalah untuk mencari nilai segi empat sama kod kunci untuk mengembangkan perbezaan antara nombor yang serupa, dan kemudian mengambil digit tengah (selalunya bit binari) mengikut panjang jadual sebagai fungsi cincang. nilai. Oleh kerana digit tengah produk berkaitan dengan setiap digit pengganda, alamat cincang yang terhasil adalah lebih seragam. Andaikan setiap kata kunci dalam set kata kunci terdiri daripada s digit (u1, u2, …, us), analisis keseluruhan set kata kunci, Dan ekstrak beberapa sama rata bit atau gabungannya sebagai alamat. Kaedah analisis digital ialah kaedah mengambil beberapa bit digital dengan nilai yang agak seragam dalam kata kunci elemen data sebagai alamat cincang. Iaitu, apabila kata kunci mempunyai banyak digit, anda boleh menganalisis bit kata kunci dan membuang bit yang tidak sekata sebagai nilai cincang. Ia hanya sesuai apabila semua nilai kata kunci diketahui. Dengan menganalisis pengedaran, julat nilai kata kunci ditukar kepada julat nilai kata kunci yang lebih kecil. Contohnya: Untuk membina jadual cincang dengan bilangan elemen data n=80 dan panjang cincang m=100. Tanpa kehilangan keluasan, kami hanya memberikan 8 kata kunci untuk analisis di sini 8 kata kunci adalah seperti berikut: K1=61317602 K2=61326875 K3=62739628 K4=61343634 K1=61317602 K2=61326875 K3=62739628 K4=61343634 K52=627668=627668=277668=257668=2000000. K8=61394220 Analisis 8 kata kunci di atas menunjukkan bahawa nilai digit ke-1, ke-2, ke-3, dan ke-6 dari kiri ke kanan kata kunci adalah agak tertumpu dan tidak sesuai sebagai alamat cincangan yang ke-4, ke-5, Ke-7, Nilai 8-bit agak sekata, dan dua daripadanya boleh dipilih sebagai alamat cincang. Katakan dua digit terakhir dipilih sebagai alamat cincang, maka alamat cincang bagi lapan kata kunci ini ialah: 2, 75, 28, 34, 15, 38, 62, 20. Anggap nilai kod kunci sebagai nombor dalam pangkalan lain dan kemudian tukarkannya menjadi nombor dalam pangkalan asal, dan kemudian pilih beberapa daripadanya sebagai alamat cincang. Shift superposisi: Jajar dan tambah bit rendah bahagian yang dibahagikan. (1) Kaedah zip Bentuk ringkas kaedah cincang adalah untuk menentukan setiap slot dalam jadual cincang sebagai ketua senarai terpaut. Semua rekod yang mencincang ke slot tertentu dimasukkan ke dalam senarai terpaut untuk slot itu. Rajah 9-5 menggambarkan jadual cincang terbuka di mana setiap slot menyimpan rekod dan penunjuk ke senarai terpaut yang lain. 7 nombor ini disimpan dalam jadual cincang dengan 11 slot, dan fungsi cincang yang digunakan ialah h(K) = K mod 11. Susunan sisipan nombor ialah 77, 7, 110, 95, 14, 75 dan 62. Terdapat 2 nilai dicincang ke slot 0, 1 nilai dicincang ke slot 3, 3 nilai dicincang ke slot 7, dan 1 nilai dicincang ke slot 9. Kaedah pencincangan tertutup menyimpan semua rekod terus dalam jadual cincang. Setiap kunci kekunci rekod mempunyai kedudukan asas yang dikira oleh fungsi cincang, iaitu, h(kunci). Jika kunci hendak dimasukkan, dan rekod lain sudah menduduki kedudukan asas R (perlanggaran berlaku), maka R disimpan di alamat lain dalam jadual, dan dasar penyelesaian konflik menentukan alamatnya. Idea asas penyelesaian konflik jadual cincang tertutup ialah: apabila konflik berlaku, gunakan kaedah tertentu untuk menjana urutan alamat cincang d0, d1, d2,...di,...dm-1 untuk kod kunci K. Antaranya, d0=h (K) dipanggil kedudukan rumah alamat asas K; semua di (0< i< m) adalah alamat cincang berikutnya. Apabila K dimasukkan, jika nod di alamat pangkalan sudah diduduki oleh elemen data lain, ia akan disiasat mengikut urutan mengikut urutan alamat di atas, dan kedudukan bebas terbuka pertama yang ditemui akan digunakan sebagai lokasi penyimpanan K ; jika semua cincang berikutnya Tiada alamat adalah percuma, menunjukkan bahawa jadual cincang tertutup penuh dan limpahan dilaporkan. Sejajar dengan itu, apabila mendapatkan semula K, jujukan alamat berikutnya dengan nilai yang sama akan dicari secara berurutan, dan kedudukan di akan dikembalikan apabila perolehan semula berjaya jika alamat bebas terbuka ditemui semasa mendapatkan semula sepanjang urutan probing, ini bermakna tiada kunci untuk dicari dalam kod jadual. Apabila memadam K, kami juga mencari secara berurutan mengikut urutan alamat pengganti dengan nilai yang sama Jika kami mendapati kedudukan tertentu di mempunyai nilai K, kami memadam elemen data pada kedudukan itu di (operasi pemadaman sebenarnya hanya menandakan. nod untuk pemadaman); Jika alamat percuma terbuka ditemui, ini bermakna tiada kunci untuk dipadamkan dalam jadual. Oleh itu, untuk jadual cincang tertutup, kaedah membina jujukan alamat cincang berikutnya ialah kaedah mengendalikan konflik. Kaedah yang berbeza membentuk probe membawa kepada kaedah yang berbeza untuk menyelesaikan konflik. Di bawah adalah beberapa kaedah pembinaan biasa. (1) Kaedah pengesanan linear menganggap jadual cincang sebagai jadual gelang Jika konflik berlaku di alamat asas d (iaitu h(K)=d), unit alamat berikut disiasat mengikut urutan: d. +1 , d+2,...,M-1,0,1,...,d-1 sehingga alamat percuma ditemui atau nod dengan kod kunci ditemui. Sudah tentu, jika anda kembali ke alamat d selepas mencari sepanjang urutan penyiasatan, ini bermakna kegagalan sama ada anda melakukan operasi sisipan atau operasi dapatkan semula. Fungsi kuar untuk kuar linear ringkas ialah: p(K,i) = i Contoh 9.7 Adalah diketahui bahawa satu set kod kunci ialah (26, 36, 41, 38, 44, 15, 68, 12, 06, 51, 25), panjang jadual cincang M = 15, gunakan linear kaedah penerokaan untuk menyelesaikan konflik dan membina jadual kunci Hash set ini. Oleh kerana n=11, gunakan kaedah yang selebihnya untuk membina fungsi cincang dan pilih nombor perdana terbesar P=13 kurang daripada M. Kemudian fungsi cincang ialah: h(kunci) = kunci%13. Masukkan setiap nod mengikut tertib: 26: h(26) = 0, 36: h(36) = 10, 41: h(41) = 2, 38: h(38) = 12, 44: h(44) = 5 . Apabila 15 disisipkan, alamat cincangnya ialah 2. Memandangkan 2 sudah diduduki oleh elemen dengan kod kunci 41, ia perlu disiasat. Mengikut kaedah probing berurutan, adalah jelas bahawa 3 adalah alamat percuma terbuka, jadi ia boleh diletakkan dalam unit 3. Begitu juga, 68 dan 12 boleh diletakkan dalam unit 4 dan 13 masing-masing (2) Kaedah kuadratik kuadratik Idea asas kaedah kuadratik ialah: alamat cincang yang dijana seterusnya tidak berterusan, tetapi Jumped. untuk memberi ruang kepada elemen data seterusnya untuk mengurangkan pengagregatan. Urutan pengesanan kaedah pengesanan sekunder ialah: 12, -12, 22, -22,... dsb. Maksudnya, apabila konflik berlaku, sinonim dicincang bolak-balik pada kedua-dua hujung alamat pertama. Formula untuk mencari alamat terbuka seterusnya ialah: (3) Kaedah probing rawak Fungsi probing yang ideal harus secara rawak memilih kedudukan seterusnya dari slot yang tidak dilawati dalam urutan probing, Iaitu, jujukan kuar mestilah pilih atur rawak bagi kedudukan jadual cincang. Walau bagaimanapun, kita sebenarnya tidak boleh memilih kedudukan secara rawak daripada jujukan siasatan kerana jujukan siasatan yang sama tidak boleh diwujudkan semasa mendapatkan kunci. Walau bagaimanapun, kita boleh melakukan sesuatu seperti probing pseudo-rawak. Dalam probe pseudo-rawak, slot ke-i dalam urutan probe ialah (h(K) + ri) mod M, di mana ri ialah jujukan nombor "rawak" antara 1 dan M - 1. Semua sisipan dan pengambilan menggunakan nombor "rawak" yang sama. Fungsi probe ialah p(K,i) = perm[i - 1], di mana perm ialah tatasusunan panjang M - 1 yang mengandungi jujukan nilai rawak dari 1 hingga M - 1. Contoh: Sebagai contoh, panjang jadual hash yang diketahui m=11, fungsi cincang ialah: H (kunci) = kunci % 11, kemudian H (47) = 3, H (26) = 4, H (60 )=5, dengan andaian kata kunci seterusnya ialah 69, kemudian H(69)=3, yang bercanggah dengan 47. Jika pengesanan linear dan kemudian pencincangan digunakan untuk mengendalikan konflik, alamat cincang seterusnya ialah H1=(3 + 1)% 11 = 4. Jika masih terdapat konflik, alamat cincang seterusnya ialah H2=(3 + 2)% 11 = 5. , masih ada konflik, terus cari alamat hash seterusnya sebagai H3 = (3 + 3)% 11 = 6, tiada lagi konflik pada masa ini, isi 69 ke dalam unit 5, lihat Rajah 8.26 (a ). Jika anda menggunakan pengesanan sekunder dan pencincangan untuk mengendalikan konflik, alamat cincang seterusnya ialah H1 = (3 + 12)% 11 = 4. Jika masih terdapat konflik, cari alamat cincang seterusnya H2 = (3 - 12)% 11 = 2. Tiada konflik pada masa ini Isi 69 ke dalam unit 2, lihat Rajah 8.26 (b). Jika pengesanan pseudo-rawak dan kemudian pencincangan digunakan untuk mengendalikan konflik, dan urutan nombor pseudo-rawak ialah: 2, 5, 9,…….., maka alamat cincang seterusnya ialah H1 = (3 + 2)% 11 = 5, dan masih terdapat konflik , kemudian cari alamat cincang seterusnya sebagai H2 = (3 + 5)% 11 = 8. Tiada konflik pada masa ini, isi 69 ke dalam unit 8, lihat Rajah 8.26 (c). (4)Kaedah pengesanan hash berganda Kedua-dua probing pseudo-rawak dan probing sekunder boleh menghapuskan masalah pengagregatan asas, iaitu, kod utama dengan alamat asas yang berbeza, dan segmen tertentu urutan probing mereka bertindih. Walau bagaimanapun, jika dua kekunci cincang ke alamat asas yang sama, jujukan siasatan yang sama masih akan diperoleh menggunakan kedua-dua kaedah dan pengagregatan masih akan berlaku. Ini kerana urutan probing yang dihasilkan oleh probing pseudo-rawak dan probing sekunder hanyalah fungsi alamat asas, bukan fungsi nilai kunci asal. Masalah ini dipanggil pengelompokan sekunder. Untuk mengelakkan pengagregatan sekunder, kita perlu menjadikan urutan probe sebagai fungsi nilai kunci asal dan bukannya fungsi kedudukan asas. Kaedah pengesanan cincang berganda menggunakan fungsi cincang kedua sebagai pemalar, melangkau istilah pemalar setiap kali dan melakukan pengesanan linear.
2. Fungsi Hash
1. Kaedah pembahagian baki
2. Kaedah pembundaran baki pendaraban
3. Kaedah segi empat sama
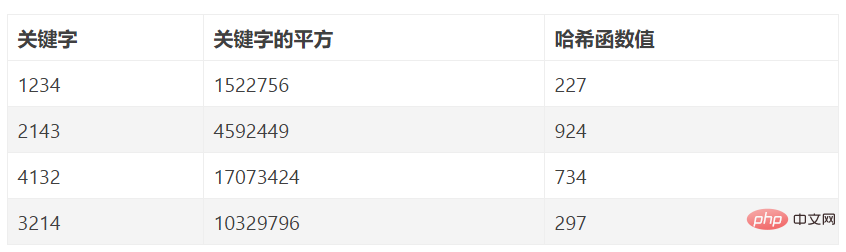
4. Kaedah analisis berangka
Kaedah ini sesuai untuk: dapat menganggar lebih awal kekerapan kejadian pelbagai nombor dalam setiap digit semua kata kunci. 5. Kaedah penukaran asas
Contoh Hash(80127429)=(80127429)13=8137+0136+1135+2134+7133+4132+2*131+9=(502432641)10 Jika anda mendapat tiga digit tengah, anda mendapat tiga digit Hash (80127429) =432
Untuk mendapatkan fungsi cincang yang baik, beberapa kaedah boleh digunakan secara gabungan, seperti menukar tapak terlebih dahulu, kemudian melipat atau menduakan, dsb. Selagi cincangan seragam, anda boleh mencantumkannya sesuka hati. . bilangan digit di bahagian terakhir boleh berbeza), dan kemudian ambil jumlah superposisi bahagian ini (menjatuhkan pembawa) sebagai alamat cincang Kaedah ini dipanggil kaedah lipatan. terbahagi kepada:
Superposisi sempadan: Lipat ke depan dan ke belakang dari satu hujung di sepanjang sempadan pembahagi, kemudian jajarkan dan tambah.
1. Kaedah senarai terpaut yang dipisahkan
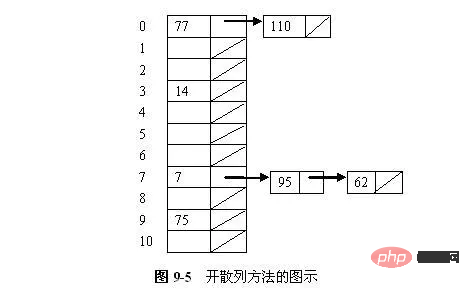
2. Kaedah pencincangan tertutup (kaedah alamat terbuka)



Atas ialah kandungan terperinci Gunakan setiap hari! Adakah anda tahu apa itu HASH?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Gunakan fungsi HashMap.size() java untuk mendapatkan saiz HashMap
- Gunakan fungsi HashMap.get() java untuk mendapatkan elemen dalam HashMap
- Kira kod cincang tatasusunan berbilang dimensi menggunakan fungsi Arrays.deepHashCode() java
- Gunakan fungsi HashMap.values() java untuk mendapatkan semua nilai dalam HashMap
- Gunakan fungsi HashMap.containsKey() java untuk menentukan sama ada HashMap mengandungi kunci yang ditentukan

